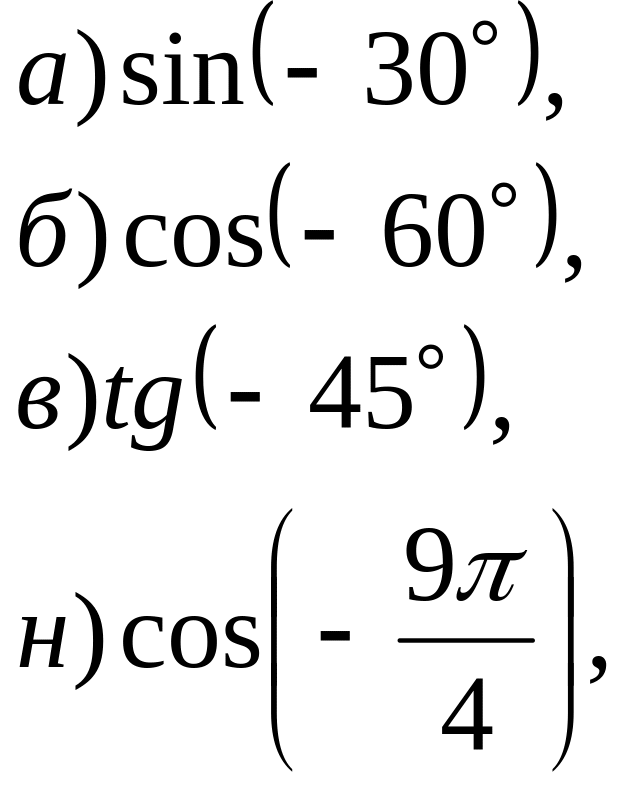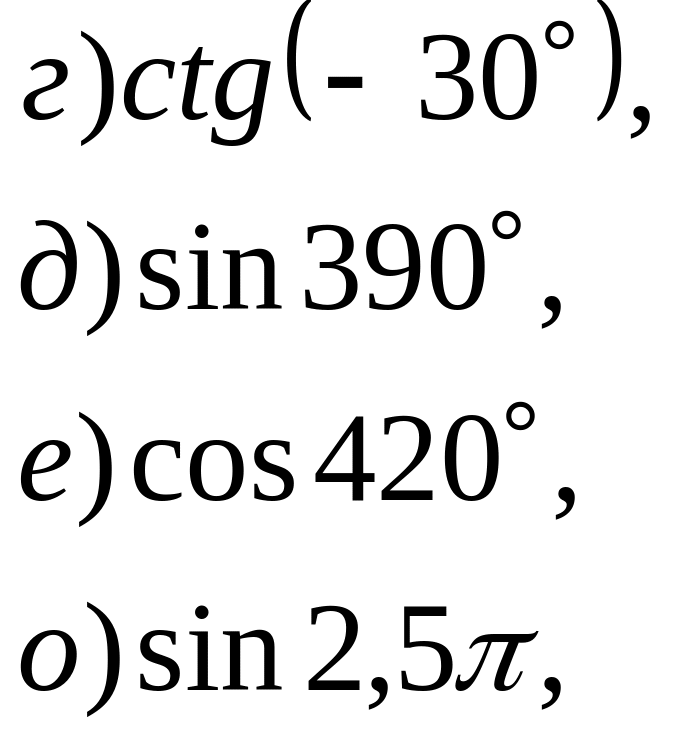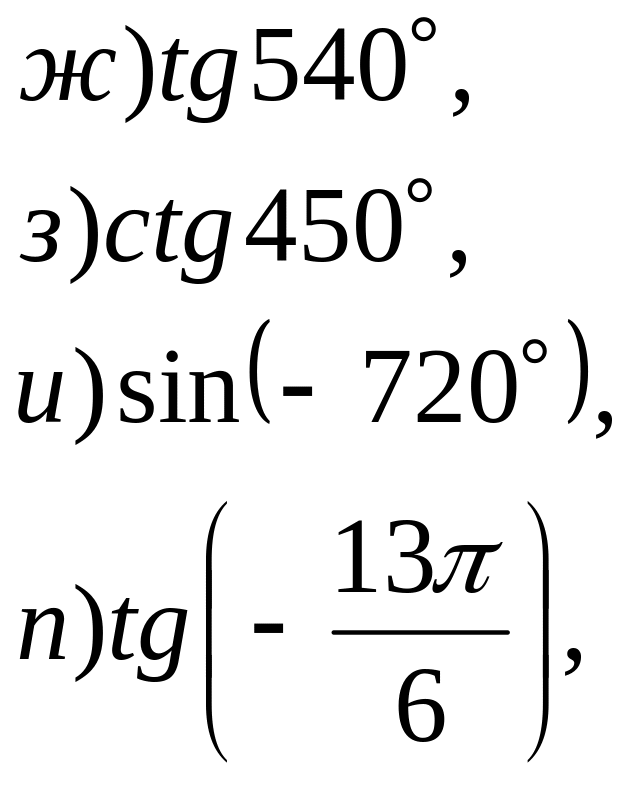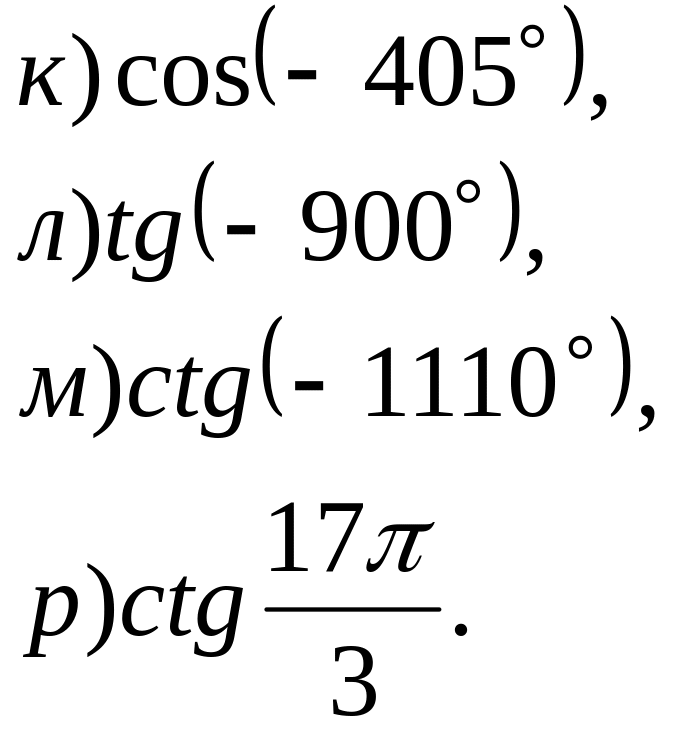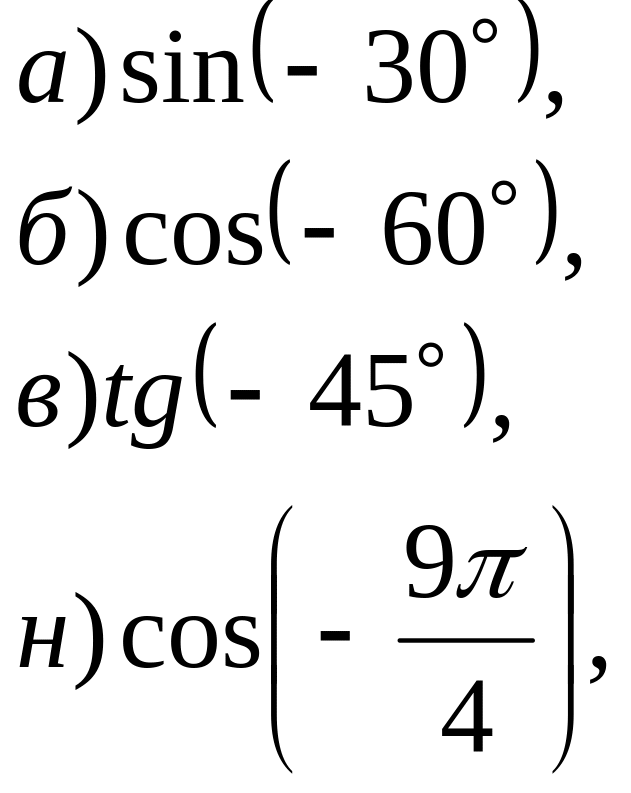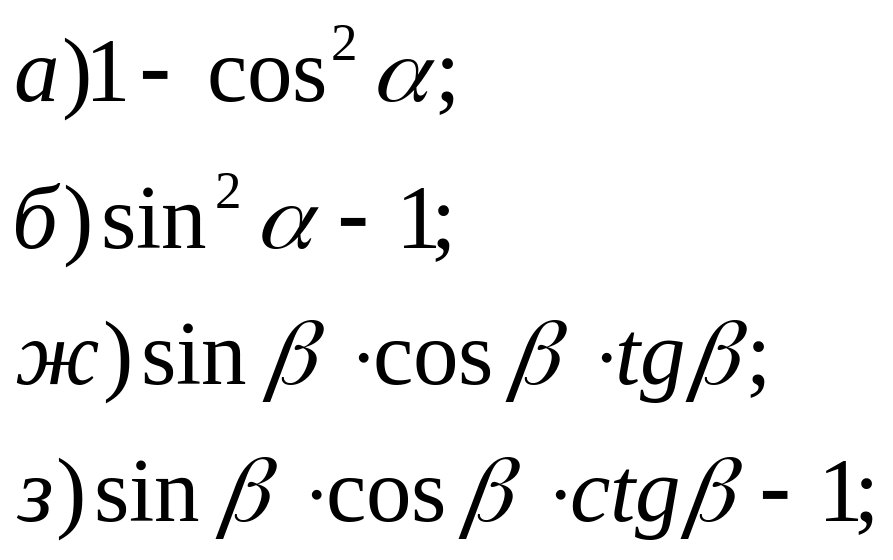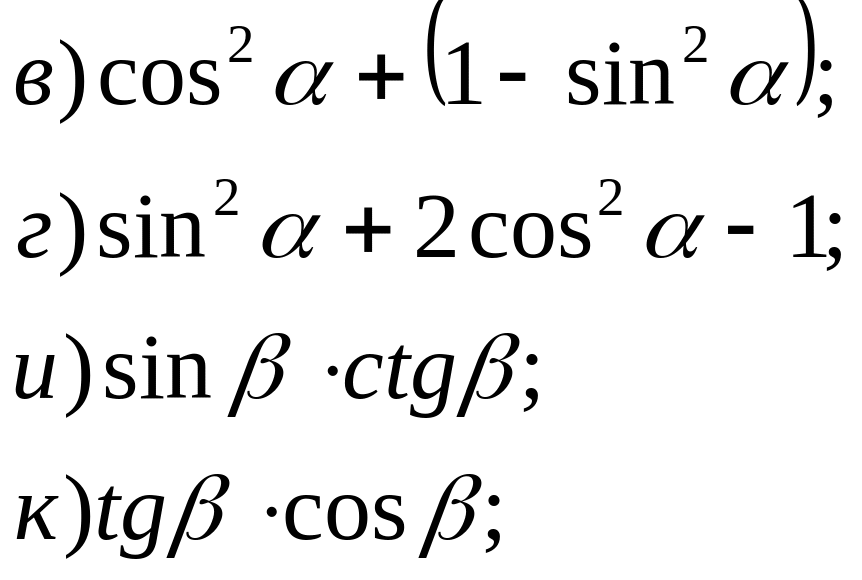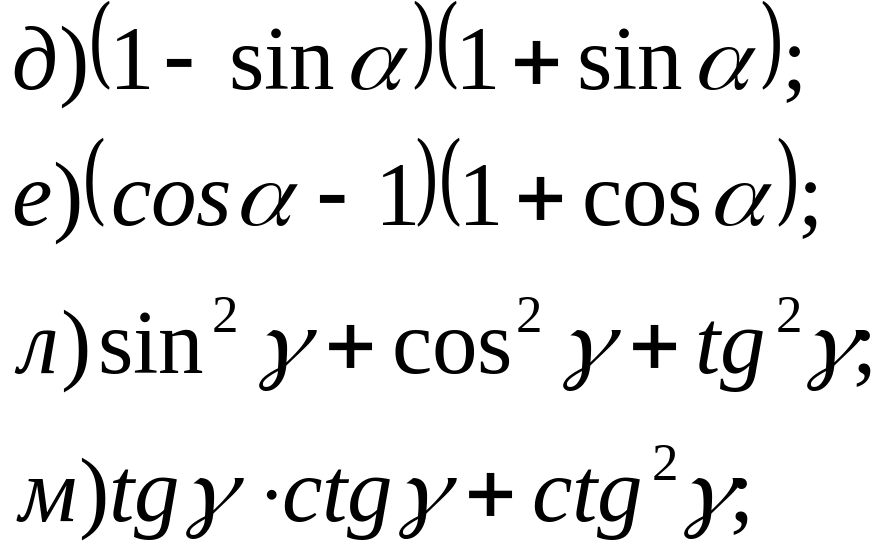- •Тригонометрические функции. Преобразования тригонометрических выражений Пособие для учащихся 11 класса
- •От автора
- •Введение
- •П. 2. Формулы перевода углов из градусной меры в радианную, и наоборот
- •П. 3. Определение тригонометрических функций
- •П. 4. Таблица значений тригонометрических функций
- •П. 5. Свойства тригонометрических функций
- •П. 6. Азбука тригонометрии
- •П. 7. Нахождение значений тригонометрических функций
- •Линия котангинса
- •П. 12. Преобразования графиков
- •П. 13. Обратные тригонометрические функции
- •П. 14. Простейшие тригонометрические уравнения
- •П. 15. Простейшие тригонометрические неравенства
- •П. 17. Формулы приведения и их применение
- •П. 18. Формулы двойного и половинного угла
- •П. 19. Формулы суммы и разности тригонометрических функций
- •III зачетный раздел Тригонометрические уравнения п. 20. Методы решения тригонометрических уравнений
- •Упрощение уравнения, используя тригонометрические формулы.
- •II. Метод введения новой переменной
- •III. Однородные тригонометрические уравнения.
- •Алгоритм отыскания производной функции :
- •Правила дифференцирования
- •П. 22. Применение производной
- •Физический смысл производной.
- •Геометрический смысл производной.
- •Алгоритм составления уравнения касательной к графику функции:
- •III. Исследование функции на монотонность и экстремум.
- •IV. Применение производной к построению графика функции.
- •V. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке .
- •Справочный раздел
- •Ответы, указания, решения
- •Литература
- •Содержание
- •Тригонометрические функции. Преобразование тригонометрических выражений
- •Г. Новокузнецк, ул.Транспортная, 17
П. 5. Свойства тригонометрических функций
Значения синуса и косинуса ограничены единицей, т.е.
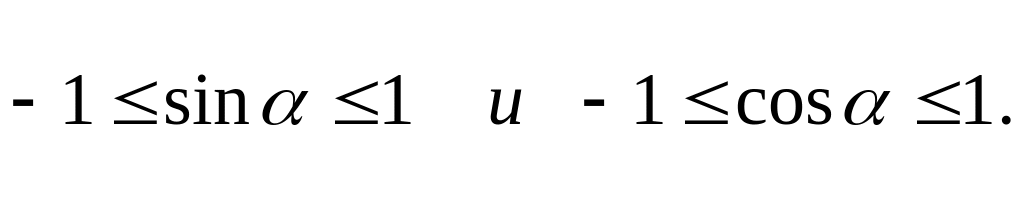
Пример:
Выражения
![]() — не имеют смысла.
— не имеют смысла.
Значения тангенса и котангенса не ограничены.
На единичной окружности в каждой из четвертей тригонометри-ческие функции сохраняют постоянный знак (рис. 6).
sin
cos
tg
и
ctg
+
+
+
+
+
+
–
–
–
–
–
–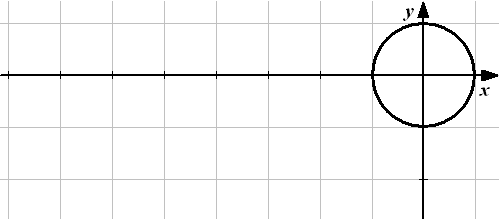
Рисунок 6
Синус, тангенс и котангенс – нечетные функции, а косинус – четная, т.е.
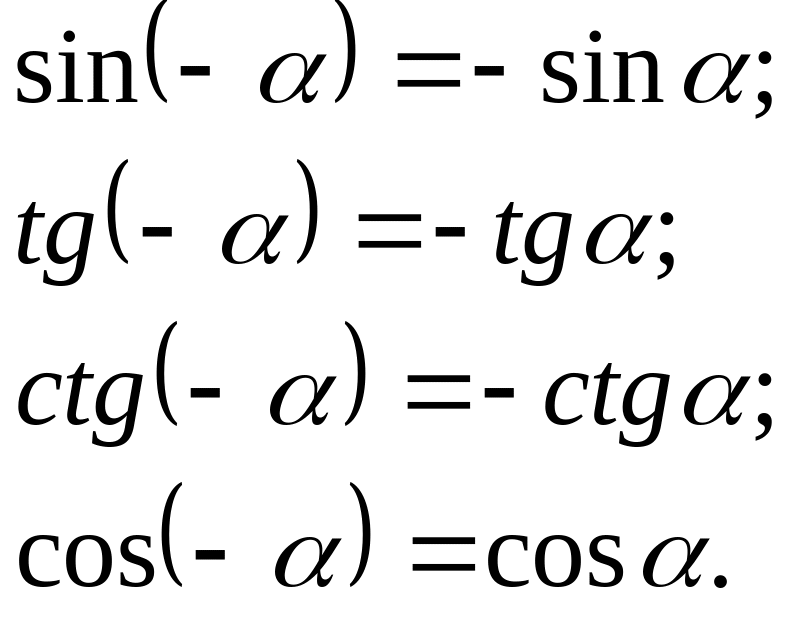
П![]() ример:
ример:
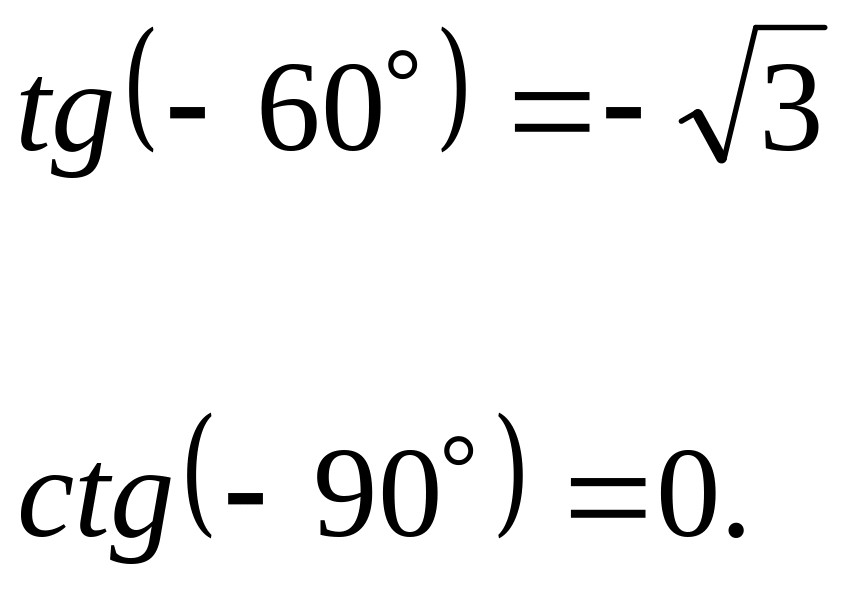
,
При изменении угла на целое число оборотов значения тригономет-рических функций не меняются.
П
ример:
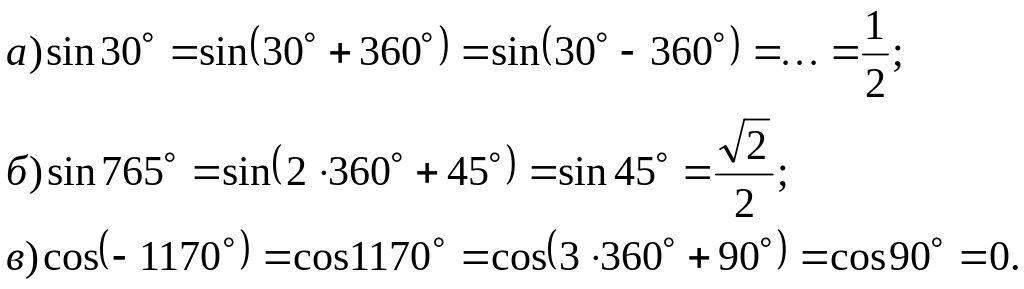
№ 9. Определите знак выражения:
![]()
![]()
![]()
![]()
№ 10. Вычислите:
|
|
|
|
№ 11. Найдите значение выражения:
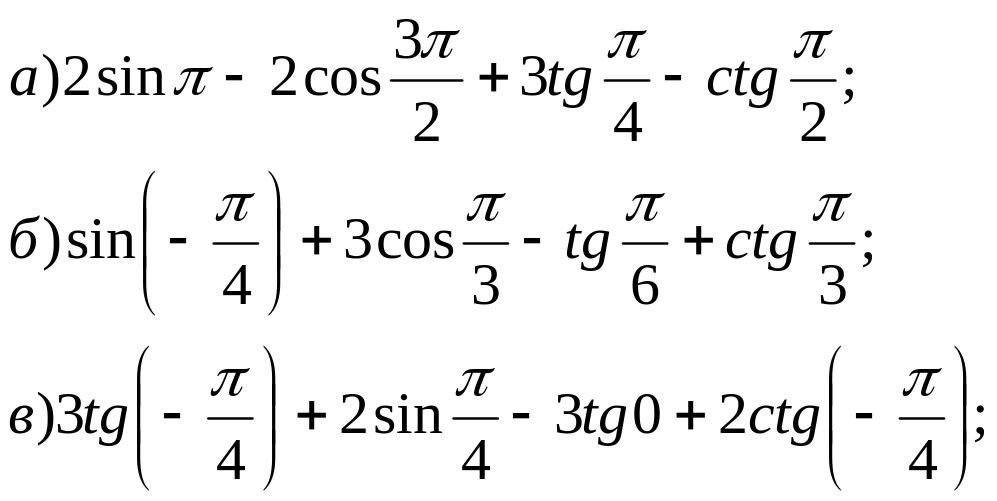
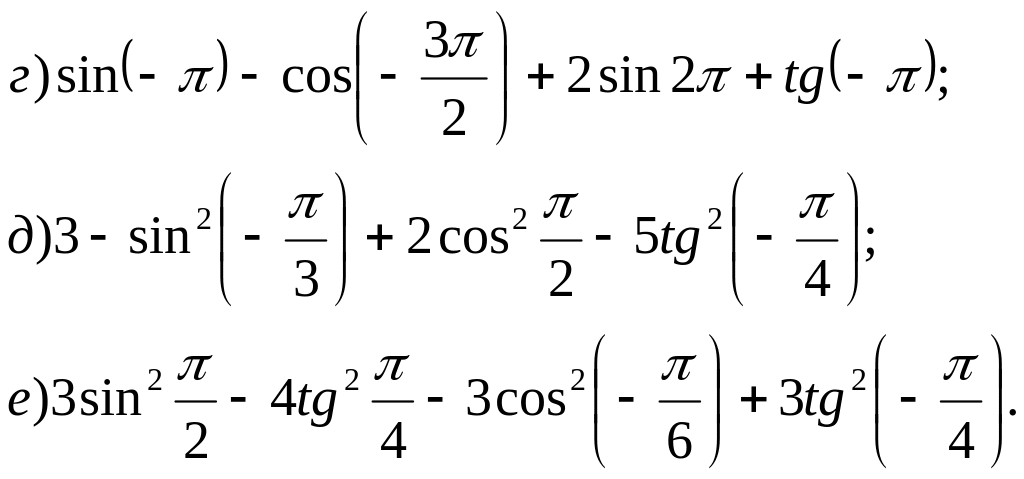
№ 12*. Вычислите:
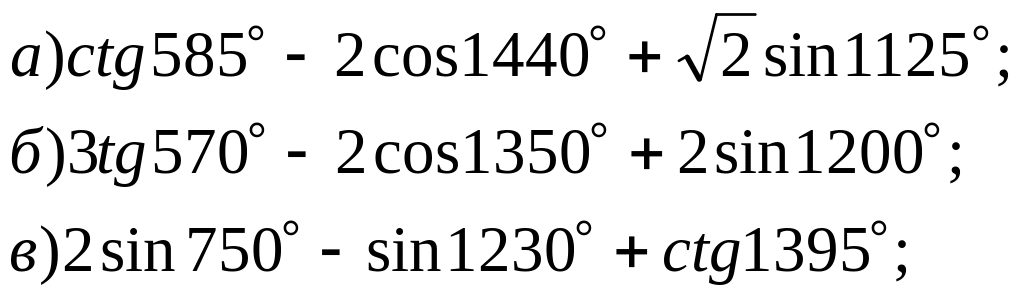

№ 13*. Найдите наибольшее и наименьшее значения функций:
![]() в) f(x)=3sinx+3;
г) f(x)=2cosx-3.
в) f(x)=3sinx+3;
г) f(x)=2cosx-3.
П. 6. Азбука тригонометрии
Введём основные тригонометрические тождества и их следствия. Рассмотрим применение формул при преобразованиях выражений, зависимости между тригонометрическими функциями одного и того же угла, а также нахождение значений тригонометрических функций по заданному значению одной из них.
Основные тригонометрические тождества (ОТТ):
(1) sin2 + cos2 = 1 — основная тригонометрическая единица
(2)
![]() —
тригонометрическая единица
—
тригонометрическая единица
(3)
![]() (4)
(4)
![]()
(5)
![]() (6)
(6)
![]()
Следствия из ОТТ:
(7)
![]() ;
(8)
;
(8)
![]()
(9)
![]() ;
(10)
;
(10)
![]()
(11)
![]() ;
(12)
;
(12)
![]() .
.
Применение формул:
1.
В формулах 7, 8, 9, 10, знаки «![]() »
зависят от того, в какой четверти
расположен угол
(см. стр. 10, свойство III, рис. 6).
»
зависят от того, в какой четверти
расположен угол
(см. стр. 10, свойство III, рис. 6).
2. Формулы 1 и 2 применяются при упрощении выражений, заменой в них 1 на соответствующие заданию тригонометрические единицы, или наоборот.
Пример:
а)
![]() ,
,
б) 1+tgx∙ctgx=1+1=2.
3.
Формулы 3, 4, 5, 6 применяются при упрощении
путем сведения выражения либо к
![]() либо к
либо к
![]() .
.
Пример1
Упростите выражение:
![]()
Используем формулу (3): .
Пример2 Докажите
тождество:
![]()
Используем
формулы (1,3,4):
![]()
![]()
![]() — ч.т.д.
— ч.т.д.
№ 14. Упростите выражения:
|
|
|
№ 15. Докажите тождество:
![]()
![]()
![]()
№ 16*. Докажите тождество:
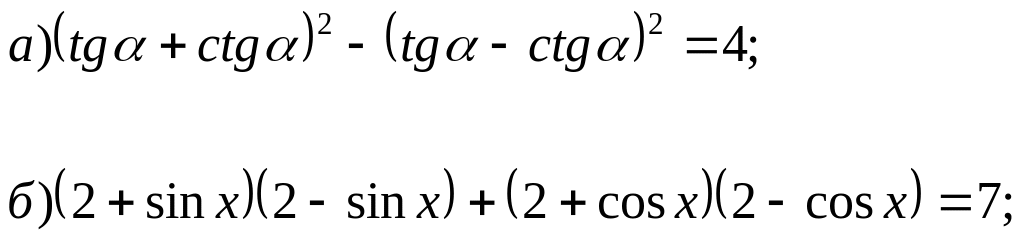
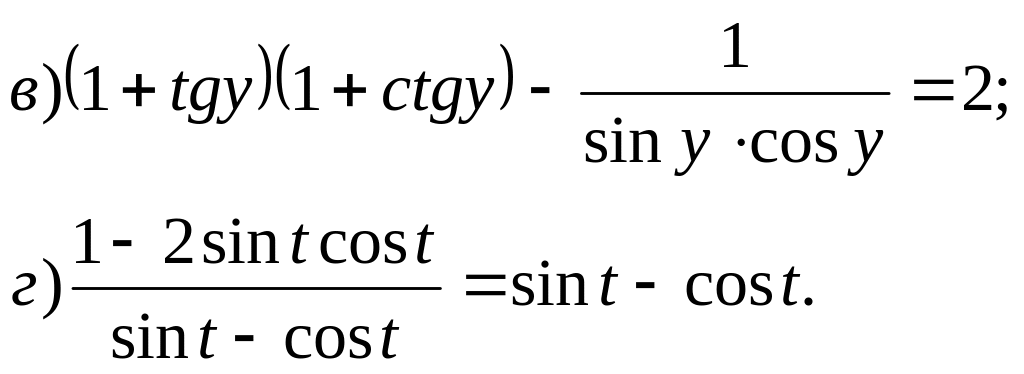
№ 17*. Найдите наибольшее значение выражения:
![]()
![]()
№ 18*.
Зная, что
![]() ,
найдите
,
найдите
![]()
№ 19*.
Зная, что
![]() ,
найдите
,
найдите
![]()
П. 7. Нахождение значений тригонометрических функций
Основная задача: по известному значению одной из функций и заданному углу найти значения остальных тригонометрических функций этого же угла.
Используются:
ОТТ (формулы 1,3,4 — стр.12);
следствия из ОТТ (формулы 7,8,9,10 — стр.12);
знаки тригонометрических в координатных четвертях (рис.3 — стр. 5; рис. 6 — стр.10).
![]()
П![]() ример
1. Найти , если известно,
что
ример
1. Найти , если известно,
что
Решение:
заметим, что
![]() четверти
(рис.3) и
четверти
(рис.3) и
![]() -
отрицательны (рис.6).
-
отрицательны (рис.6).
Из формулы 8 имеем:
![]()
![]()
Из формулы 3:
![]() .
.
Из формулы 12:
![]() .
.
Заметим, что если
известно значение
![]() ,
то вычисления аналогичны.
,
то вычисления аналогичны.
Пример 2.
Известно, что
![]() .
Вычислите
.
Вычислите![]() .
.
Решение:
![]() четверти,
четверти,
![]() .
.
Из формулы 12:
![]() .
.
Из формулы 10:
![]() .
.
Из формулы 7:
![]() .
.
№ 20. Найдите значения тригонометрических функций угла , если известно, что:
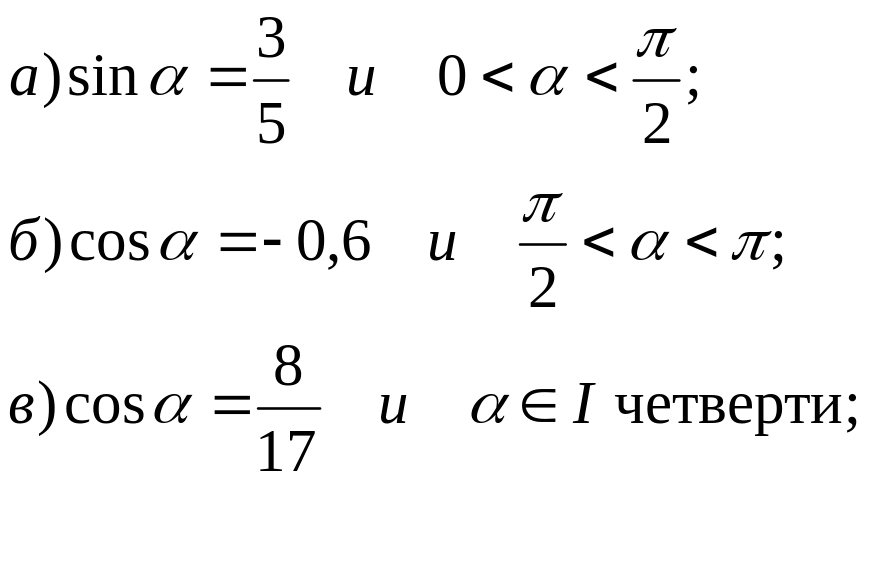
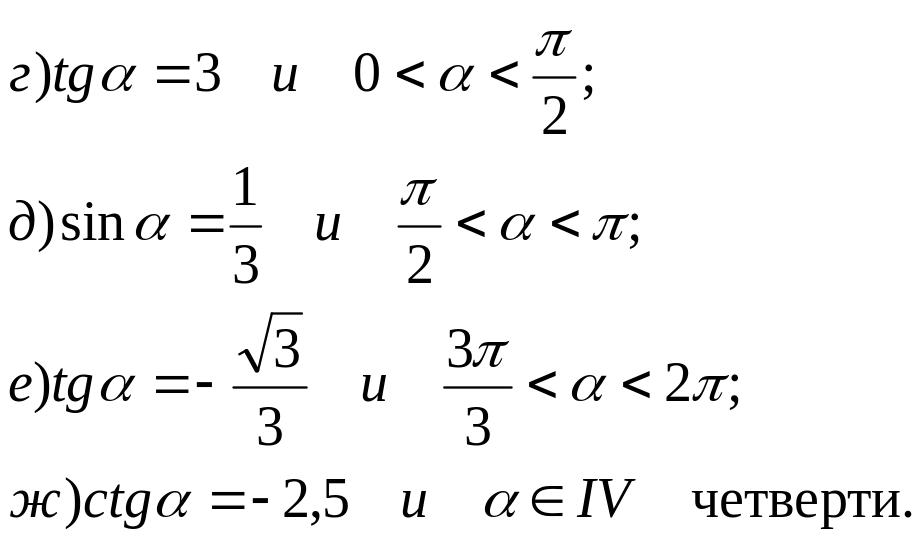
№ 21*. Найдите значение дроби:
![]()
![]()
п. 8. Функция y = sin x, её свойства и график
Заметим,
что т.к.
![]() ,
то при построении графиков тригоно-метрических
функций в качестве единичного отрезка
удобнее выбирать 1см; соответственно
= 3 см;
,
то при построении графиков тригоно-метрических
функций в качестве единичного отрезка
удобнее выбирать 1см; соответственно
= 3 см;
![]() = 1,5 см;
= 1,5 см;
![]() =
6 см и т.д.
=
6 см и т.д.
Этапы построения
графика
![]() (синусоида
рис.7):
(синусоида
рис.7):
Точки функции на
отрезке
![]() .
.
Замечание:
При построении графика на отрезке
![]() удобнее использовать точки
удобнее использовать точки
![]()
Рисунок 7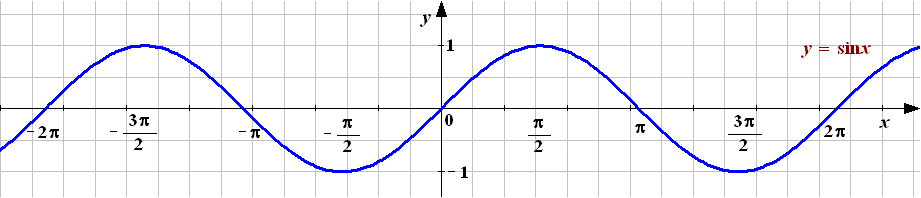
Свойства функции .
Функция периодическая; основной период равен 2 , т.е. через каждый промежуток 2 значения функции и соответственно график повторяются.
Функция нечетная, т.е.
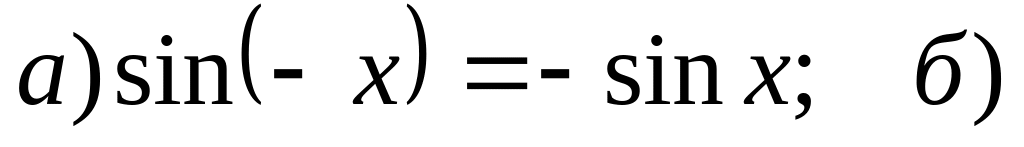 график
симметричен относительно начала
координат.
график
симметричен относительно начала
координат.
Следующие свойства можно определять как по единичной окружности (рис.8), так и по графику (рис.7).
Т.к.
а)
Функция возрастает на
б)
Функция убывает на
![]() то очевидно, что:
то очевидно, что:![]() ;
кєΖ
;
кєΖ![]() ;
кєΖ
;
кєΖ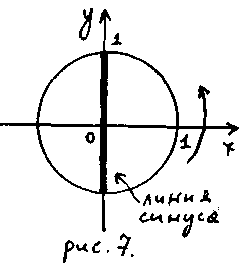
линия
синуса
Рисунок 8
в)
Функция положительна на
![]() ;
кєΖ,
;
кєΖ,
г)
Функция отрицательна на
![]() ;
кєΖ,
;
кєΖ,
д)
Нули функции 0,
,-
,…![]() ;
кєΖ.
;
кєΖ.
п. 9. Функция y = cos x, её свойства и график
Построение графика
функции
![]() и проводится аналогично графику функции
,
учитывая сдвиг вдоль оси OX
на
.
и проводится аналогично графику функции
,
учитывая сдвиг вдоль оси OX
на
.
Рисунок 9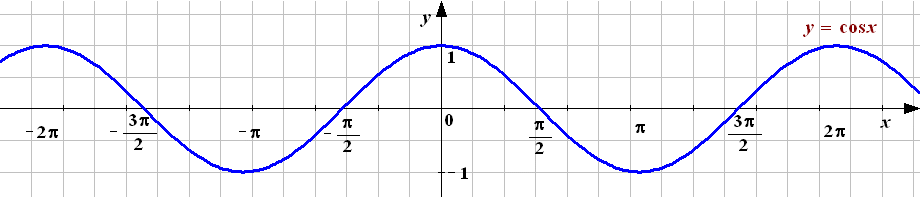
Свойства функции (синусоида).
1.
![]()
2.
![]()
3. Функция периодическая с основным периодом 2 .
4.
Функция четная, т.е.
![]() график
симметричен относительно оси OY.
график
симметричен относительно оси OY.
Рисунок 10
линия
косинуса
а)
Функция возрастает на
кєΖ,
б)
Функция убывает на
в)
Функция положительна на

![]() ;
;![]() ;
кєΖ,
;
кєΖ,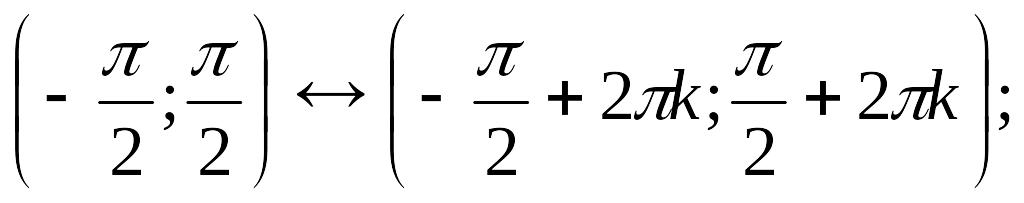 кєΖ,
кєΖ,![]() то (см. рис. 9 и рис.10):
то (см. рис. 9 и рис.10):
г)
Функция отрицательна на
![]() ;
кєΖ,
;
кєΖ,
д)
Нули функции
![]() ;
кєΖ.
;
кєΖ.
п. 10. Функция y = tg x, её свойства и график
Этапы построения
графика
![]() (тангенсоида
рис.11):
(тангенсоида
рис.11):
Контрольные
точки на
![]() .
.
Рисунок 11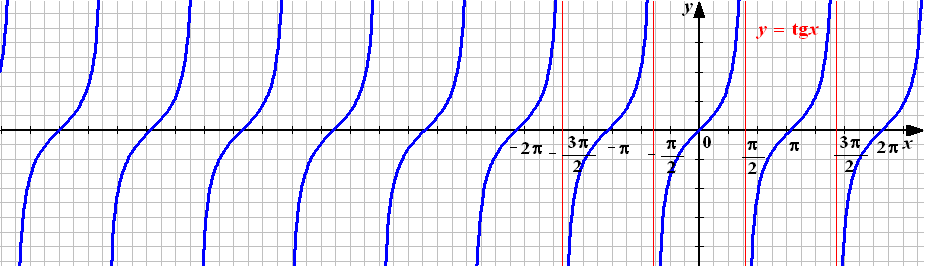
Свойства функции .
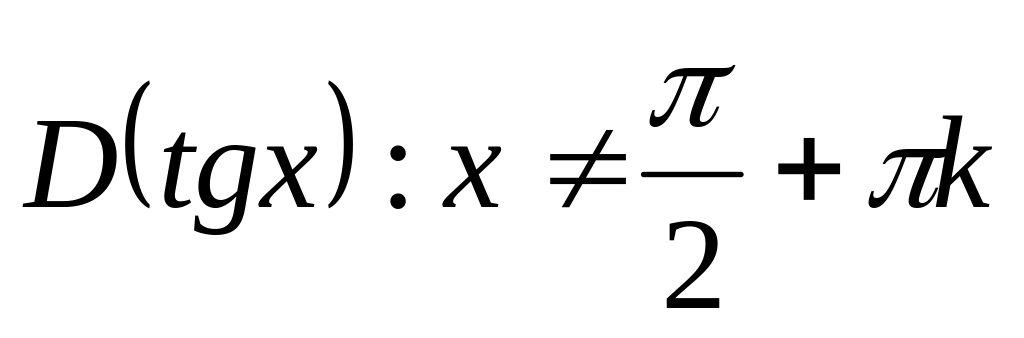 ,
кєΖ.
,
кєΖ.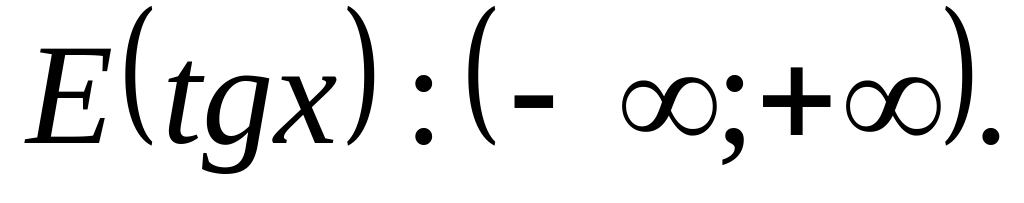
Функция периодическая с основным периодом .
Функция нечетная.
Если
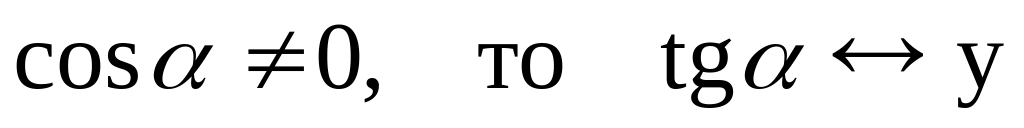 и (см. рис.11 и рис.12):
и (см. рис.11 и рис.12):
а)
Функция возрастает на
(с увеличением
б)
Функция положительна на
г)
Нули функции
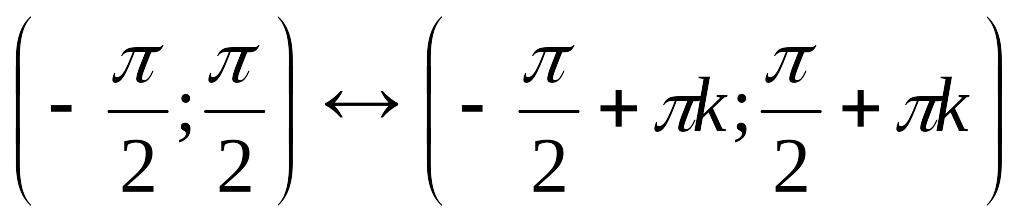
![]() ,
у – увеличивается), кєΖ;
,
у – увеличивается), кєΖ;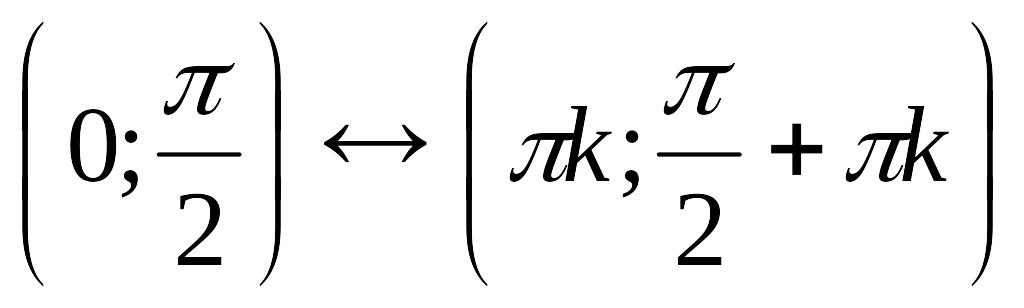 ,
в)
Функция отрицательна на
,
в)
Функция отрицательна на
![]()
![]() кєΖ.
кєΖ.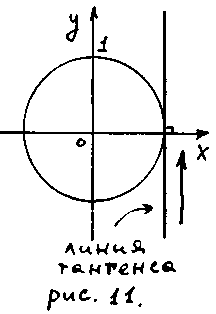
линия
тангенса
Рисунок 12
п. 11. Функция y = ctg x, её свойства и график
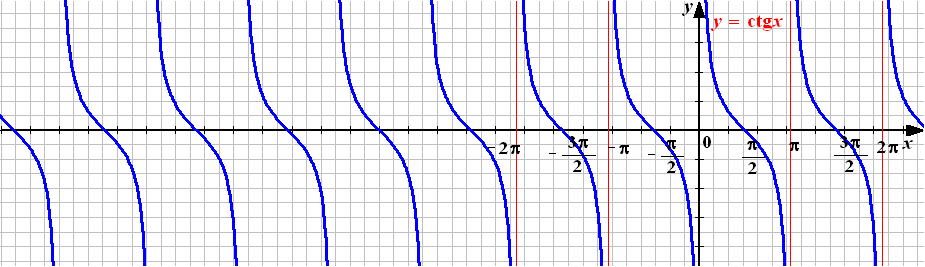
Рисунок 13
Свойства функции
![]() (тангенсоида).
(тангенсоида).