П. 2. Формулы перевода углов из градусной меры в радианную, и наоборот

Пусть заданная дуга на единичной окружности содержит угол n - в градусах, или – в радианах. Тогда:

(*) — формула перевода углов из градусной меры угла

в радианную,

(**) — формула перевода углов из радианной меры угла

в градусную.

№ 2. Вычислите радианную меру угла, равного:

а) б) в)

Решение: а) используем формулу (*)

№ 3. Найдите градусную меру угла, равного:

а) б) в)

Решение: а) используем формулу (**)

Остальные задания № №2, 3 выполните самостоятельно.

П. 3. Определение тригонометрических функций

В курсе геометрии были определены синус, косинус и тангенс угла от до 90º. Теперь мы расширим эти определения на случай произвольного угла и определим котангенс угла.

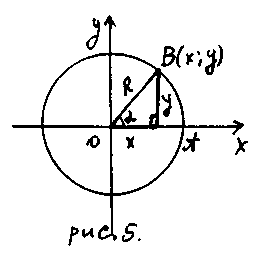
Пусть на произвольной окружности (рис. 5) при повороте на угол начальный радиус ОА переходит в произвольный радиус ОВ и точка В имеет координаты (х; у).

З

Рисунок 5

аметим, что координаты точки В образуются с помощью задания прямоугольного треугольника, в котором х и у – катеты, а гипотенуза R – радиус заданной окружно-

сти.

●Синусом угла называется отношение ординаты точки В к длине радиуса окружности: .

●Косинусом угла называется отношение абсциссы точки В к длине радиуса окружности: .

●Тангенсом угла называется отношение ординаты точки В к её абсциссе: .

●Котангенсом угла называется отношение абсциссы точки В к её ординате: .

Замечания:

1. Синус, косинус, тангенс и котангенс – тригонометрические функции.

2. Значения тригонометрических функций зависят только от градусной меры угла и не зависят от х, у и R.

3. Выражение имеет смысл при , т.е. кроме углов: (см. рис. 5).

4. Выражение ctg имеет смысл при , т.е. кроме углов: (см. рис. 5).

5. Если тригонометрические функции определять на единичной окружности (R=1), то , а .

№ 4. Для прямоугольного выпишите, как определяются тригонометрические функции углов А и В.

№ 5*. Используя данные № 4, найдите АС, АВ и А, если = , ВС=12см.

П. 4. Таблица значений тригонометрических функций

Значения тригонометрических функций можно определять по таблицам М.В. Брадиса, но в тригонометрии чаще используются углы, содержащиеся в следующей таблице:

nо	0о	30о	45о	60о	90о	120о	135о	150о	180о	210о	225о	240о	270о	300о	315о	330о	360о
	0								π
sin α	0				1				0	-			-1			-	0
cos α	1				0	-			-1			-	0				1
	0		1		—	-	-1		0		1		—	-	-1		0
	—		1		0		-1		-		1		0		-1	-	—

Заметим, что

№ 6. Вычислите:

Решение:

№ 7. Найдите значение выражения:

Решение:

№ 8*. Найдите значение выражения: