V. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке .

1. найти ;

2. найти точки, в которых или выбрать из них те, которые лежат внутри отрезка ;

3. вычислить значения функции в полученных точках и на концах отрезка;

4. выбрать наибольшее значение функции и наименьшее, они обозначаются:

Пример 7. Найдите наименьшее и наибольшее значение функции на отрезке .

Р ешение:

Производная функции:

Критические точки, лежащие в заданном отрезке:

Значения функции в критической точке и на концах отрезка:

,

,

.

Выберем из этих значений наименьшее и наибольшее:

№ 77. Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку М графика функции f(x):

№ 78. Напишите уравнение касательной к графику функции f(x) в точке с абсциссой :

№ 79. Найдите точки графика функции f(x), в которых касательная параллельна оси абсцисс:

№ 80*. Найдите угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой .

№ 81*. К функции проведены касательные в точках с абсциссами . Являются ли эти касательные параллельными?

№ 82*. Найдите критические точки функции и укажите одну точку минимума.

№ 83*. Найдите критические точки функции и укажите одну точку максимума.

№ 84*. Исследуйте функцию на возрастание и убывание.

№ 85*. Найдите наибольшее и наименьшее значения функции на отрезке .

№ 86*. Найдите точки, в которых скорость изменения функции меньше скорости изменения функции .

№ 87*. Найдите промежутки возрастания (убывания) функции .

Справочный раздел

1. Формулы сокращенного умножения.

2. Степень и её свойства.

,

10) ,

3. Решение линейного уравнения.

1. Помножить обе части уравнения на наименьший общий знаменатель, входящих в него дробей (если они есть).

2. Раскрыть скобки (если они есть), используя правила:

3. Собрать выражения, содержащие неизвестную слева от знака равенства, а числа – справа. При этом, если выражение (число) переносится через знак равенства, то оно меняет знак с «+» на «-», и наоборот.

4. Привести подобные слагаемые.

5. - простейшее линейное уравнение

Пример: НОЗ: 15

5

3

15

Ответ: – 9.

4. Решение квадратного уравнения.

- дискриминант;

если , то уравнение имеет два корня:

если , — уравнение имеет один корень второй кратности:

если , — уравнение не имеет корней.

Пример:

Ответ: 1; 1,5.

Заметим, что если какой-либо из коэффициентов b или c отсутствует, значит, он равен нулю.

5. Решение дробно–рационального уравнения.

1. Найти общий знаменатель дробей, входящих в уравнение (НОЗ);

2. Вычислить область определения уравнения (ООУ: НОЗ 0);

если этот этап вызывает затруднения, то в конце необходимо

сделать проверку

3. Умножить обе части уравнения на НОЗ;

4. Решить полученное уравнение;

5. Исключить из решения посторонние корни (см. п. 2).

П

х

х–5

1

ример:

- посторонний корень.

Ответ: -2.

6. Решение систем уравнений (метод подстановки).

1. В линейном уравнении выразить одну из неизвестных.

2. Подставить выраженную неизвестную в другое уравнение.

3. Решить полученное уравнение с одной неизвестной.

4. Найти значение второй неизвестной.

Пример:

Ответ: (2;-2).

7. Решение линейных неравенств.

Линейное неравенство решается так же, как решается линейное уравнение, но:

1. при умножении (делении) обеих частей неравенства на отрицательное число, нужно сменить знак неравенства;

2. при изображении решения неравенства на координатной прямой следует пользоваться таблицей:

знаки	точки	скобки
>; <	○	( … ; … )
	●	[ … ; … ]

Пример:

- 1 x

Ответ: .

8. Решение квадратных неравенств.

1. Найти точки пересечения параболы с осью OX,

т.е. решить уравнение: .

2. На координатной плоскости схематически построить параболу, ветви которой направлены вверх, если ; и вниз, если .

3. Выписать решения, соответствующие знаку неравенства: — часть параболы, расположенная выше оси OX; — часть параболы, расположенная ниже оси OX.

При изображении точек и записи ответа использовать таблицу (см. п. VII).

Пример:

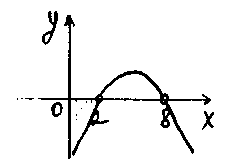
— ветви вниз х є ( 2 ; 8 )

Ответ: ( 2 ; 8 ).

9. Функция и её свойства.

1. Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y. При этом: x – независимая переменная (аргумент); y – зависимая переменная (значение функции). Обозначается:

2. Все значения независимой переменной образуют область определения функции. Обозначается: .

   1. Если , где — многочлен, то R – множество действительных чисел,

   2. Если , где — многочлены, то ,

   3. Если , где — многочлен, то

3. Все значения, которые принимает зависимая переменная, образуют область значений функции. Обозначается: .

4. Графиком функции называют множество всех точек координатной плоскости (х; у), абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

5. Функция называется возрастающей на J, если для любых , таких, что верно , т.е. график на J – «ползет вверх».

6. Функция называется убывающей на J, если для любых , таких, что верно , т.е. график на J – «падает вниз».

7. Функция положительна на J, если для любого верно неравенство , т.е. график на J расположен выше оси ОХ.

8. Функция отрицательна на J, если для любого верно неравенство , т.е. график на J расположен ниже оси ОХ..

9. Значения аргумента, в которых значения функции равны нулю, называются нулями функции, т.е. точки в которых график функции пересекает ось ОХ.

Пример: Выпишите свойства функции , график которой изображен на рис. 21.

Решение:

3. возрастает на

4. убывает на

5. положительна на

6. отрицательна на

7. Нули функции:

Рисунок 21