2. Геометрический смысл производной.

Пусть задана функция и точка, принадлежащая графику этой функции . Тогда:

- формула, задающая уравнение касательной к графику функции , проходящей через точку с абсциссой .

Алгоритм составления уравнения касательной к графику функции:

1. Обозначить абсциссу точки касания;

2. Вычислить ;

3. Найти 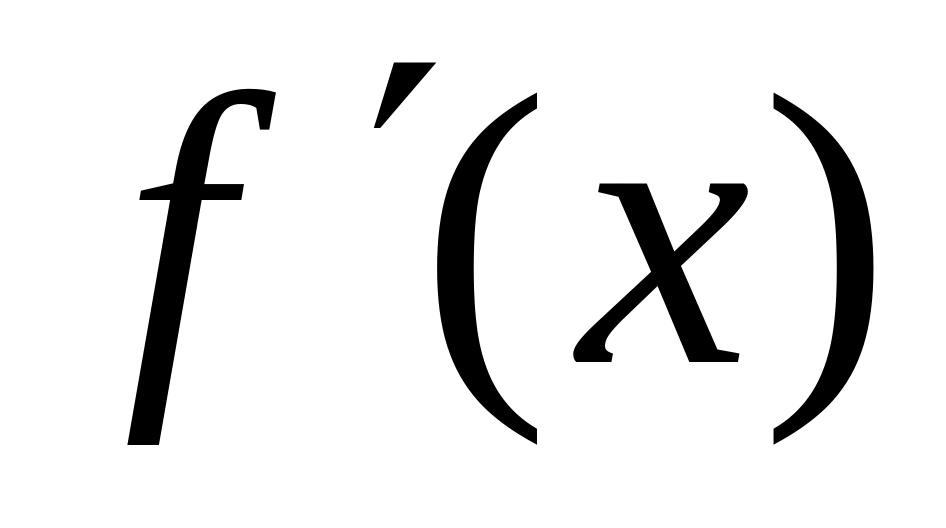и вычислить ;

4. Подставить найденные значения , , в формулу и упростить полученное выражение.

- тангенс угла наклона касательной к оси OX — геометрический смысл производной, (угловой коэффициент прямой).

Если , то функция возрастает в окрестности точки ;

если , то функция убывает в окрестности точки ;

если , то касательная к графику параллельна оси OX в точке .

Пример 2. Дана функция . Найдите тангенс угла наклона касательной к оси OX, проходящей через точку .

Решение:

Ответ: .

Пример 3. Составьте уравнение касательной к графику функции в точке с абсциссой – 2.

Решение:

Ответ: .

Пример 4. Вычислите точки графика функции , в которых касательная параллельна оси OX.

Решение:

— условие параллельности касательной к оси OX,

,	т.е. прямой y=0, угловой коэффициент которой равен 0.

Ответ:

III. Исследование функции на монотонность и экстремум.

1. найти область определения функции;

2. найти производную функции ;

3. найти критические точки функции:

   1. решить уравнение ,

   2. найти область определения производной ;

4. отметить критические точки на числовой прямой и определить знак производной на каждом промежутке;

5. определить промежутки монотонности функции:

   1. если на некотором промежутке, то на этом промежутке функция — возрастает,

   2. если на некотором промежутке, то на этом промежутке функция — убывает;

6. о пределить точки экстремума функции, используя схемы (где х₀ – критическая точка):

х₀ – точка минимума х₀ – точка максимума экстремума нет

Пример 5. Исследуйте на монотонность и найдите точки экстремума функции .

Решение:

1. R, т.к функция — многочлен;

2. ;

3. Критические точки:

   1. 

   2. R, т.к производная функции — многочлен;

4,5) Определение промежутков монотонности функции:

+

+

–

— возрастает на ,

— убывает на ;

6. Точки экстремума функции:

и значение функции в точках экстремума

IV. Применение производной к построению графика функции.

1. найти область определения функции;

2. выяснить, является ли функция четной или нечетной, является ли периодической;

3. найти точки пересечения графика функции с осями координат;

4. определить промежутки знакопостоянства функции;

5. найти промежутки монотонности функции (см.п.III);

6. найти точки экстремума и значение функции в этих точках;

7. исследовать поведение функции в «особых» точках и при

Пример 6. Исследуйте функцию и постройте ее график

Решение:

1) , т.е. график функции не пересекает прямые х = –2 и х = 2 — вертикальные асимптоты.

2) Функция не периодична.

Т.к. и — совпадают, то функция является четной, т.е. ее график симметричен относительно оси ОХ.

3) Точки пересечения графика с осями координат

с осью ОХ: у = 0. Имеем:

Т.е.

с осью ОУ: х = 0. Имеем:

4) Промежутки знакопостоянства (используем метод интервалов)

Н

ули функции —

— положительна на , т.е. график функции расположен выше оси ОХ;

— отрицательна на , т.е. график функции расположен ниже оси ОХ.

5) Монотонность функции

Критические точки:

а) ;

б)

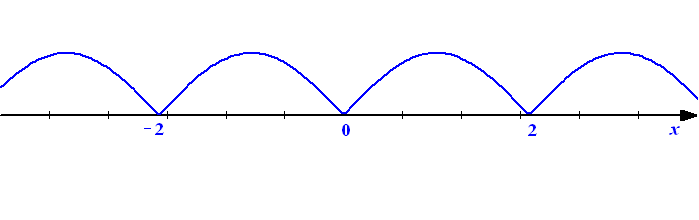
— возрастает на ,

— убывает на .

6) Экстремумы функции

и значение функции в этой точке

7) Исследование функции при больших значениях аргумента

При и при , т.е. график функции не пересекает прямую у = 1 — горизонтальная асимптота.

Используя данные п.п. 1)–7) строим график функции