Муниципальное вечернее (сменное) общеобразовательное учреждение

«Вечерняя (сменная) общеобразовательная школа № 1»

Тригонометрические функции. Преобразования тригонометрических выражений Пособие для учащихся 11 класса

Издательство МОУ ДПО ИПК

Новокузнецк

2010

ББК 22.151.0 я 72 Печатается по решению

Т 67 редакционно-издательского

совета МОУ ДПО ИПК

Тригонометрические функции. Преобразование тригонометрических выражений : пособие для учащихся 11 класса вечерней сменной школы / составители : С. Ю. Белый, Г. И. Макаренко. – 2-е изд., испр. – Новокузнецк : Изд-во МОУ ДПО ИПК, 2010. – 87 с.

Рецензенты:

С. Н. Суханова, кандидат педагогических наук, декан фа­куль­тета профессиональной переподготовки муниципаль­ного образовательного учреждения дополнительного профессионального образования «Институт повышения квалификации», г. Новокузнецк; Л. В. Алексеенко, методист ОО «Математика» муниципального образовательного учреждения дополни­тельного про­­фессионального образования «Научно-мето­дический центр», г. Кемерово.

В пособии представлен опыт преподавания тригонометрии на уроках и консультациях в 11 классах очной и очно-заочной форм обучения. Планирование соответствует традиционной последовательности изучения тем в вечерней школе, реализуется МВ(С)ОУ «ВСШ № 1» г. Новокузнецка Кемеровской области.

Учебное пособие предназначено для учреждений данного типа.

ББК 22.151.0 я 72

© Белый С.Ю., Макаренко Г.И., 2006

Т

От автора

Основная цель данного пособия – помочь учащимся 11-х классов вечерних (сменных) школ научиться (в том числе и самостоятельно) решать базовые задания по тригонометрии: находить значения тригонометрических функций, применять тригонометрические формулы при преобразованиях выражений, решать тригонометрические уравнения и неравенства, строить графики и проводить исследования тригонометрических функций с помощью производной; а также всем желающим проверить и закрепить свои знания по тригонометрии.

Учебный материал разделён на четыре зачётных раздела в соответствии с традиционной для вечерних школ последовательностью прохождения тем. На каждую изучаемую в пособии тему (см. «Оглавление») отводится определённое количество часов, соответствующих заочной форме обучения. Количество часов для очной формы обучения увеличивается вдвое и предусматривает рассмотрение большего материала на уроках. В пособии есть разделы: «Ответы, указания, решения» к заданиям и тестам, контролирующие правильность их выполнения; «Справочный материал», направленный на ликвидацию возможных затруднений учащихся. Приводимые в пособии формулы и утверждения даются без выводов и доказательств, их при необходимости можно найти, воспользовавшись учебными изданиями, перечисленными в разделе «Литература».

Введение

Термин «тригонометрия» происходит от греческих слов «тригоном»- треугольник и «метрио» - измерять, что в свою очередь означает «измерение треугольников». Основная задача тригонометрии состоит в решении треугольников. Так как любую задачу геометрии можно свести к решению треугольников, то тригонометрия охватывает своими применениями всю планиметрию и стереометрию и широко применяется во всех отделах естествознания и техники. Потребность в решении треугольников раньше всего возникла в астрономии. В течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии, с её помощью люди научились предсказывать солнечные и лунные затмения, использовали тригонометрические сведения для определения недоступных расстояний и положения корабля в море или каравана в пустыне.

Буквенные обозначения тригонометрических функций, которыми мы пользуемся, ввёл швейцарец по происхождению, долгие годы работавший в России и являющийся членом Петербургской академии наук, Леонард Эйлер (1707–1783). После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться с помощью формул; решаются различного рода уравнения и неравенства; составляются функции и проводятся их исследования. Изучение в физике и технике различных колебательных процессов: движение маятника часового механизма, колебание струны музыкального инструмента, колебание воды от брошенного в неё камня и т.п., также связаны с тригонометрическими функциями. Наиболее простые колебательные движения – гармонические колебания, происходящие во времени, которые можно описать с помощью функций вида: или , где – амплитуда,  – частота, - начальная фаза, Т= – период гармоничного колебания. Задавая, таким образом, с помощью функции модель какого-либо физического процесса и, проводя её подробное исследование, можно в дальнейшем утверждать: как будет изменяться данный процесс с течением времени, от чего зависит это изменение и как на это изменение можно влиять. Всё это широко используется в науке, различных отраслях народного хозяйства и развитии технического прогресса.

I ЗАЧЕТНЫЙ РАЗДЕЛ

Тригонометрические функции и тождества

Простейшие тригонометрические уравнения

п. 1. Радианное измерение углов

При изложении многих вопросов в курсе математики и физики, а также на практике удобно пользоваться радианной системой измерения угловых величин.

Д

Углом в 1 радиан называется угол поворота начального радиуса на длину дуги окружности равную радиусу (рис.1), т.о.

1 рад _,

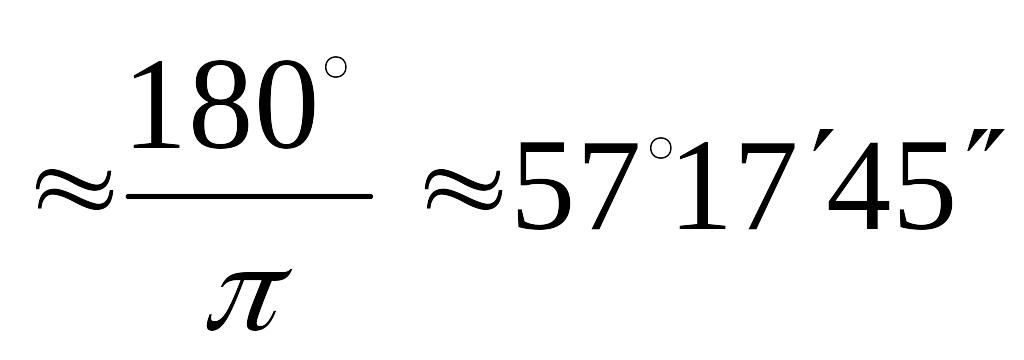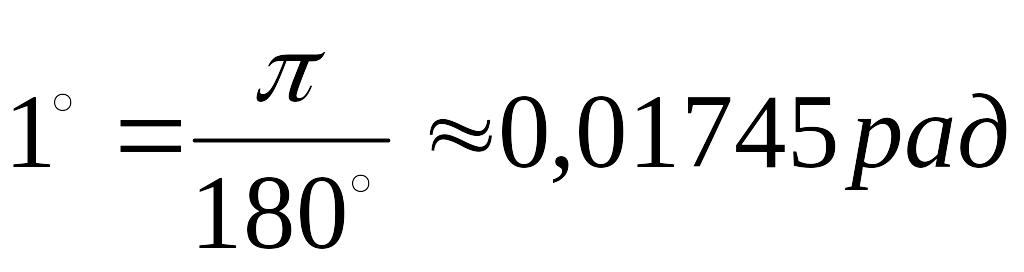
Очевидно, что угол в радиан равен 180 ,

ля введения радианной меры зададим на координатной плоскости XOY окружность с центром в начале координат и радиусом R=1 — единичную окружность. И пусть радиус, совпадающий с положительной полуосью OX, называется начальным радиусом ОА.

т

Рисунок 1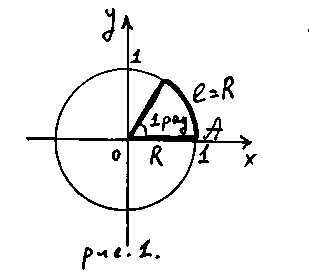

.о. справедливы равенства:

Выделим три замечания:

1. При повороте начального радиуса против часовой стрелки угол поворота считают положительным; а при повороте по часовой стрелке – отрицательным (рис. 2).

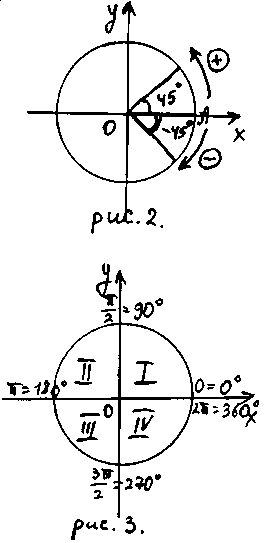
2. Рисунок 2

   Оси координат делят единичную окружность на четыре четверти (квадранты) (рис. 3).

I четверть: образуют углы от 0 до 90 , т.е. (о; );

II четверть: от 90 до 180 , т.е. ( ; );

III четверть: от 180 до 270 , т.е. ( ; );

IV четверть: от 270 до 360 , т.е. ( ;2 )

Рисунок 3

Отметим, что углы 0 ; 90 ; 180 ; 270 ; 360

не относятся ни к какой из четвертей.

2. Угол поворота начального радиуса может выражаться в градусах (радианах) каким угодно действительным числом от - до + .

№ 1. Определите в какой четверти лежит заданный угол и покажите его образ на единичной окружности: 545 ; - ; 9; -1820 ; ; -230 ; 1080 .

Решение:

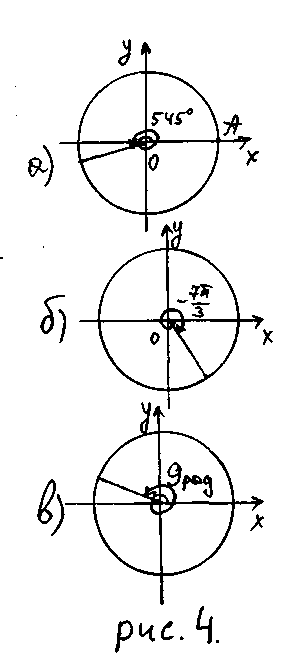545 =360 +185 , заметим, что начальный радиус ОА, проходя через точку А на единичной окружности, вновь проходит I и II четверти и останавливается в III четверти. Следовательно, образ угла 545 лежит в III четверти и соответствует углу 185 (рис. 4а).

- = -2 - , и его образ соответствует углу

- IV четв. (рис. 4б).

9=9рад EMBED Equation.3 образ соответствует углу 156 II четв. (рис.4в).

Остальные задания выполните самостоятельно.

Рисунок 4