Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5173 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Тверской Государственный Технический Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Задания на КР до ДМ.doc
Скачиваний:
1
Добавлен:
01.04.2025
Размер:
382.98 Кб
Скачать
☆
►Содержание►

  1. Элементы комбинаторики

  1. Доказать, что мощность булеана конечного множества А равна .

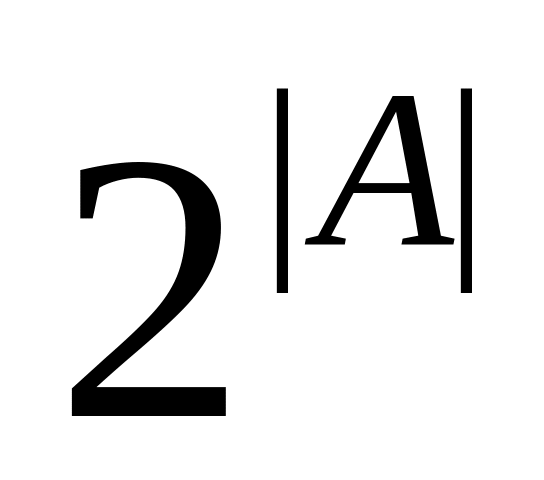  2. Определить максимальное число переборов при попытке взлома пароля, состоящего из 32 двоичных символов.

  3. Сколькими способами можно расположить на шахматной доске 8 ладей, чтобы они не могли бить друг друга.

  4. Сколькими способами можно указать на шахматной доске два квадрата: белый и черный?

  5. Сколькими способами можно указать на шахматной доске два квадрата без ограничения цвета квадратов?

  6. Сколькими способами можно выбрать три краски из имеющихся пяти?

  7. Из колоды, содержащей 52 карты, вынули 10 карт. В скольких случаях среди этих карт не окажется ни одного туза? В скольких случаях в числе этих десяти карт окажется:

    1. ровно один туз?

    2. хотя бы один туз?

    3. ровно два туза?

  1. Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?

  2. Найти число векторов , координаты которых удовлетворяют условиям:

9.1.

9.2.

9.3.

  1. Каково число матриц из n строк и m столбцов с элементами из множества {0,1}?

  2. Каково число матриц из n строк и m столбцов с элементами из множества {0,1}, у которых строки попарно различны?

  3. Доказать следующие свойства биномиальных коэффициентов:

12.1.

12.2.

12.3.

12.4. Доказать, что возрастает по n при фиксированном k.

  1. Определить мощность множества АВ, если |A|=n, |B|=m.

  2. Сколько существует бинарных отношений между элементами множеств А и В, если |A|=n, |B|=m?

  3. Сколько имеется функций из А в В, если |A|=n, |B|=m?

  4. Сколько имеется 1-1 – функций из множества А в множество В, если |A|=n, |B|=m?

  5. При каких значениях m и n существует взаимнооднозначное отображение f:AB, если |A|=n, |B|=m?

  6. Определить мощность множества вершин единичного n-мерного куба.

  7. Найти двоичный вектор с номером 50+n, где n номер Вашего варианта

  8. Чему равно число наборов удовлетворяющих условию ?

  9. Показать, что для любых 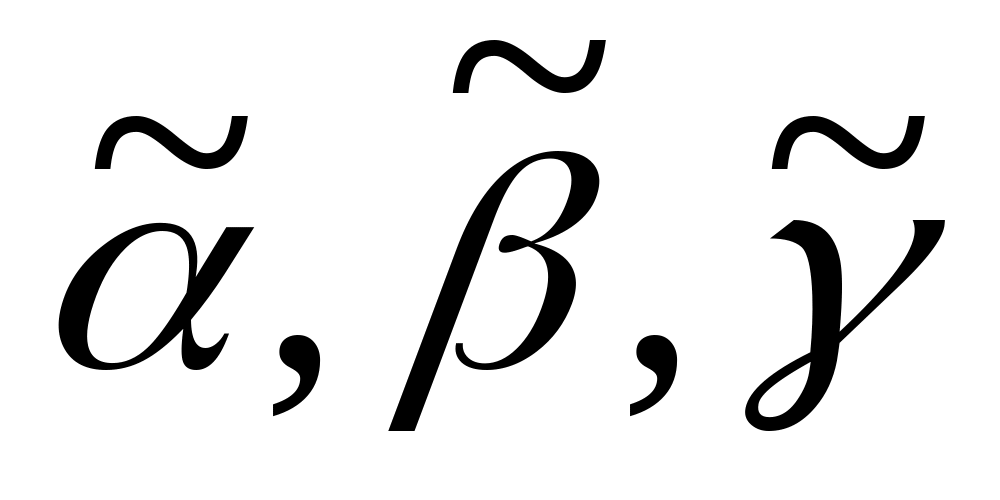из справедливы соотношения:

  10. Найти длину СДНФ функции

Варианты заданий на курсовую работу по дискретной математике

N

п/п

I

II

III

IV

V

VI

VII

1

1.1, 2.1,

4.1, 5.1,

14.9

1.1, 3, 4.1, 11.9,

7

1.17, 2.1,

5, 7, 9.1, 16.10, 17.1

7,14

1.1, 2.4, 3.7, 7.1, 9

1.1, 3.1, 4.1, 5

1, 9.1, 14, 21.4

2

1.2, 2.2, 4.2, 5.2,

14.8

1.2, 5.1, 4.2, 11.8,

8

1.16, 6, 2.2, 10, 9.2, 16.9,

17.2

6, 13

1.2, 2.3, 3.6, 7.2, 10.1

1.2, 3.2, 4.2, 5

2, 9.2, 15, 22.1

3

1.3, 2.3, 7, 9.4,

14.7

2.1, 5.2, 4.3, 11.6,

9

1.15, 8, 2.3, 9.3, 11.1, 16.8,

17.1

5, 11.1

1.3, 2.2, 3.5, 7.3, 10.2

1.3, 3.3, 4.3, 5

3, 9.3, 16, 22.2

4

1.4, 2.4, 6.1, 11,

14.6

2.2, 5.3, 4.4, 11.5,

10.1

1.14, 6, 2.4, 7, 9.1, 16.7,

17.2

4, 11.2

1.4, 2.1, 3.4, 7.4, 11

1.4, 3.4, 4.4, 5

4, 10, 17, 22.3

5

1.5, 6.2, 9.1, 12,

14.5

2.3, 5.4, 4.5, 11.4,

10.2

1.13, 5, 2.5, 9.2, 10, 16.10,

17.1

3, 11.3

1.5, 3.3, 2.20, 12, 8.1

1.5, 3.5, 4.5, 5

5, 11, 18, 21.1

6

1.6, 3.3, 8.2, 9.2, 14.1

2.4, 3, 6.1, 11.3,

10.3

1.12, 6, 2.6, 9.3, 11.2, 16.5, 17.2

2, 12.1

1.6, 2.9, 3.2, 8.2, 10.3

1.6, 3.6, 4.6, 5

6, 12.1, 19, 21.2

7

3.1, 5.1, 9.3, 13, 14.2

2.5, 5.2, 4.7, 11.2,

7

1.11, 8, 2.7, 9.1, 7, 16.4,

17.1

1, 12.2

1.7, 3.1, 2.18, 8.3, 9

1.7, 3.7, 4.7, 5

7.1, 12.2, 20, 21.3

8

3.2, 5.2, 9.4, 12, 14.3

1.2, 5.3, 4.8, 11.1,

8

1.10, 5, 2.8, 10, 9.2, 16.3,

17.2

14, 12.3

1.8, 4.2, 2.17, 5, 10.1

1.8, 3.8, 4.8, 5

7.2, 12.3, 21.1, 14

9

3.3, 8.1, 9.5, 11, 14.4

2.4, 5.1, 4.9, 11.9,

9

1.9, 2.9, 6, 11.1, 9.3, 16.2,

17.1

13, 1

1.9, 4.1, 2.16, 6, 11

1.9, 3.9, 4.9, 5

7.3, 12.4, 21.2, 15

10

1.1, 2.1, 7, 4.2, 3.2, 14.5

1.1, 5.4, 4.10, 11.8,

10.1

1.8, 3.1, 5, 9.1, 7, 16.1, 17.2

12.3, 10

1.10, 12, 2.15, 7.1, 3.15

1.10, 5, 3.10, 4.10

8, 13, 21.3, 16

11

1.2, 2.2, 3.1, 6.1, 14.5

2.1, 5.3, 4.11, 11.7,

10.2

1.7, 3.2, 6, 9.2, 10, 16.10,

17.1

12.2, 2

1.11, 7.2, 10.2, 2,14, 3.14

1.11, 5, 3.11, 4.11

1, 9.1, 14, 21.4

12

1.2, 2.2, 4.1, 9.7, 14.6

2.2, 5.2, 4.12, 11.6,

10.3

1.6, 3.3, 8, 11.2, 9.3, 16.9,

17.2

12.1, 3

1.12,2.13, 3.13, 7.3, 9.2

1.12, 3.12, 4.12, 5

2, 9.2, 15, 22.1

13

1.3, 2.3, 4.2, 9.8, 14.7

2.3, 5.1, 4.13, 11.5,

7

1.5, 3.4, 6, 7, 9.1, 16.8, 17.1

10, 4,

1.13, 2.12, 3.12, 7.4, 10.3

1.13, 3.13, 4.13, 5

3, 9.3, 16, 22.2

14

1.4, 6.2, 9.9, 11, 14.9

2.4, 3, 4.14, 11.4,

8

1.4, 3.5, 5, 10, 9.2, 16,7, 17.2

11.3, 5

1.14, 2.11, 11 3,11, 8.1

2.1, 3.14, 4.14, 5

4, 10, 17, 22.3

15

1.5, 2.2, 8.2,,9.11, 14.8

2.5, 5.4, 4.15, 11.3,

9

1.3, 3.6, 6, 11.1, 9.3, 16.9,

17.1

11.2, 6

1.15, 2.10, 3.10, 8.2, 12

2.2, 3.15, 4.15, 5,3

5, 11, 18, 21.1

16

1.6, 2.1, 4.2, 7,

14.9

1.2, 5.3, 4.16, 11.2,

10.1

1.2, 2.1, 7, 8, 9.1, 16.5, 17.1

11.1, 7

1.16, 2.9, 3.9, 8.3, 9

2.3, 3.16, 4.1, 55

6, 12.1, 19, 21.2

17

2.3, 3.1, 7, 9.1, 10,

14.1

1.1, 5.2, 4.17, 11.1,

10.2

1.1, 2.2, 6, 10, 9.2, 16.4, 17.2

8, 11.1

1.17, 2.8, 3.8, 5, 10.3

2., 3.17, 4.11, 5

7.1, 12.2, 20, 21.3

18

1.6, 2.4, 5.1, 9.2, 14.2

2.5,5.1, 4.18, 11.7,

10.3

1.11, 5, 2.3, 11.2, 9.3, 16.3,

17.1

7, 11.2

1.18, 2.7, 3.7, 6, 8.1

2.5, 3.18, 4.10, 5

7.2, 12.3, 21.1, 14

19

3.3, 2.3, 5.2, 9.3, 12

2.4, 3, 6.1, 11.9,

7

1.12, 2.4, 6, 7, 9.1, 16.2, 17.2

6, 11.3

1.19, 2.6, 3.6, 7.1, 11

2.6, 3.19, 4.9, 5

7.3, 12.4, 21.2, 15

20

1.1, 4.2, 8.1, 9.1, 14.3

2.3, 5.2, 6.2, 11.8,

8

1.13, 2.3, 8, 11.1, 9.2, 16.1,

17.1

5, 13

1.20, 2.5, 3.5, 7.2, 12

2.7, 3.20, 4.8, 5

8, 13, 21.3, 16

21

1.2, 8.1, 9.4, 10, 14.3

2.2, 5.3, 6.3, 11.6,

9

1.14, 3.1, 5, 11.2, 9.2, 16.8,

17.2

4, 14

1.21, 2.4, 3.4, 7.3, 9

2.8, 3.21, 4.7, 5

1, 9.1, 14, 21.4

22

1.3, 3.3, 9.4, 6.1, 14.4

2.1, 5.4, 6.4, 11.5,

10.1

1.15, 7, 3.2, 6, 9.1, 16.9,

17.1

3, 11.1

1.22, 2.3, 3.3, 7.4, 10.1

2.7, 3.22, 4.6, 5

2, 9.2, 15, 22.1

23

1.4, 2.2, 9.4, 6.2, 14.5

1.2, 3, 6.5, 11.4,

10.2

1.16, 10, 3.3, 8, 16.10,

17.2

2, 11.2

1.23, 2.2, 3.2, 8.1, 10.2

2.10, 3.23, 4.5, 5

3, 9.3, 16, 22.2

24

1.5, 2.4, 8.1, 9.5, 14.6

1.1, 5.1, 4.18, 11.3,

10.3

1.17, 3.4, 11.1, 9.3, 16.7, 17.2

1, 11.3

1.24, 2.1, 3.1, 8.2, 11

2.11, 3.24, 4.15, 5

4, 10, 17, 22.3

25

1.6, 3.3, 8.2, 9.2, 14.1

2.4, 3, 6.1, 11.3,

10.3

1.12, 6, 2.6, 9.3, 11.2, 16.5, 17.2

2, 12.1

1.6, 2.9, 3.2, 8.2, 10.3

1.6, 3.6, 4.6, 5

5, 11, 18, 21.1

26

3.1, 5.1, 9.3, 13, 14.2

2.5, 5.2, 4.7, 11.2,

7

1.11, 8, 2.7, 9.1, 7, 16.4,

17.1

1, 12.2

1.7, 3.1, 2.18, 8.3, 9

1.7, 3.7, 4.7, 5

6, 12.1, 19, 21.2

27

3.2, 5.2, 9.4, 12, 14.3

1.2, 5.3, 4.8, 11.1,

8

1.10, 5, 2.8, 10, 9.2, 16.3,

17.2

14, 12.3

1.8, 4.2, 2.17, 5, 10.1

1.8, 3.8, 4.8, 5

7.1, 12.2, 20, 21.3

28

2.3, 3.1, 7, 9.1, 10,

14.1

1.1, 5.2, 4.17, 11.1,

10.2

1.1, 2.2, 6, 10, 9.2, 16.4, 17.2

8, 11.1

1.17, 2.8, 3.8, 5, 10.3

2.4, 3.17, 4.11, 5

7.2, 12.3, 21.1, 14

29

1.6, 2.4, 5.1, 9.2, 14.2

2.5,5.1, 4.18, 11.7,

10.3

1.11, 5, 2.3, 11.2, 9.3, 16.3,

17.1

7, 11.2

1.18, 2.7, 3.7, 6, 8.1

2.5, 3.18, 4.10, 5

7.3, 12.4, 21.2, 15

30

3.3, 2.3, 5.2, 9.3, 12

2.4, 3, 6.1, 11.9,

7

1.12, 2.4, 6, 7, 9.1, 16.2, 17.2

6, 11.3

1.19, 2.6, 3.6, 7.1, 11

2.6, 3.19, 4.9, 5

8, 13, 21.3, 16

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности