6.3 Винтовые поверхности
Винтовые поверхности образуются при сложном винтовом движении прямой образующей, когда каждая ее точка вращается вокруг оси, а один конец этой образующей равномерно перемещается по этой оси.
Определитель такой поверхности:
Σ (ℓ, i, H, φ ), где ℓ – образующая; i – ось; Н – шаг винтовой линий; φ - угол наклона образующей к оси.
Поверхность, образованная при вращательном движении прямой образующей, наз-ся геликоидом. В зависимости от угла наклона образующей к оси геликоид может быть прямым (φ = 900) и наклонным (φ ≠ 900). Если образующая пересекается с осью вращения поверхности, геликоид называют закрытым, если не пересекается – открытым.
Данная поверхность называется прямой геликоид (φ = 900)
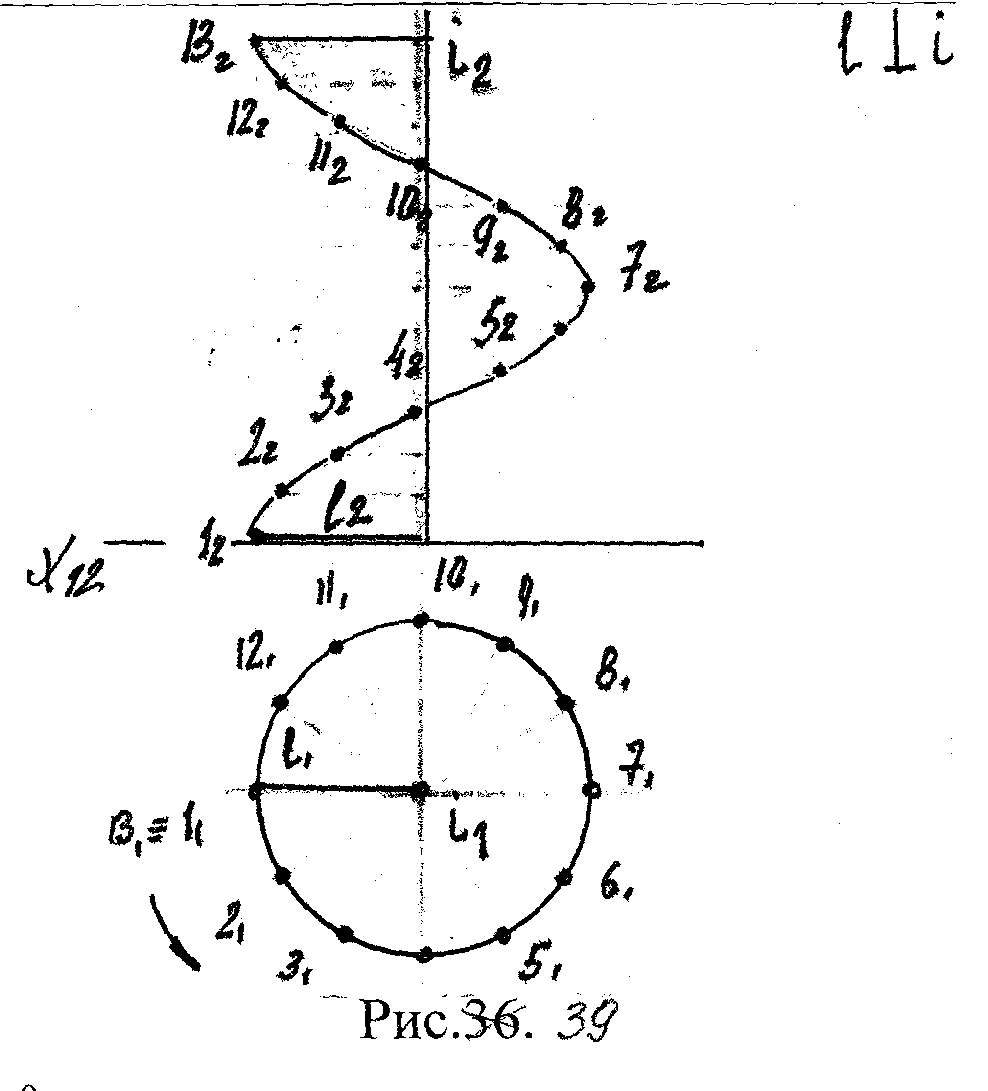
Рис.34.
Если φ ≠ 900, то геликоид наклонный).
6.4 Поверхности вращения
Образуются вращением произвольной кривой вокруг неподвижной оси.
В состав определителя пов-ти вращ-я входит образующая а, и ось вращения m, при условии вращения этой образующей вокруг оси.
Каждая точка образующей а(А,В,С,D) при вращении вокруг оси m описывает окр-ть с центром на оси вращения. Эти окр-ти наз-ся параллелями.
Н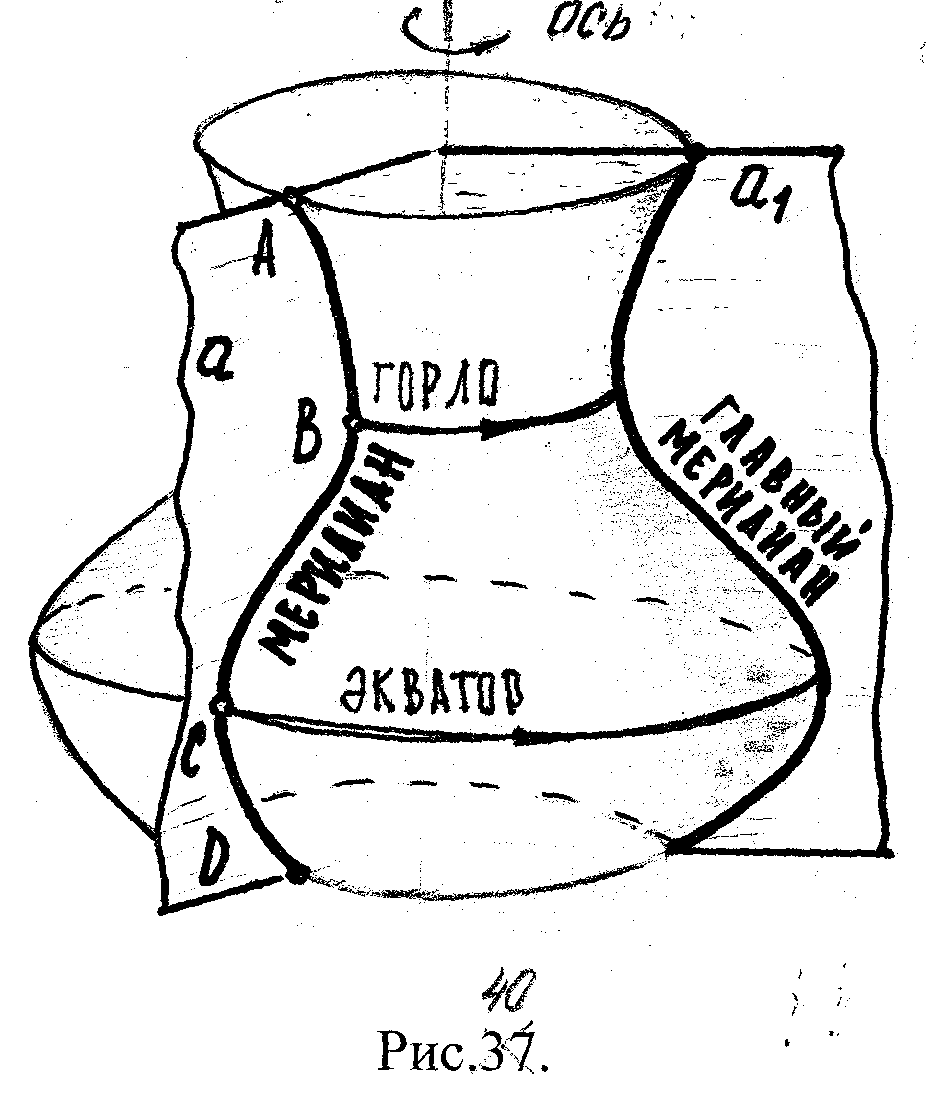
аибольшую
и наименьшую параллель поверхности
называют экватором
и горлом.
Линии, по которым пл-ти, проходящие через ось вращения пересекают поверхности наз-ют меридианами. Главн. меридиан получен в результате пересе-чения пов-ти пл-тью, ||-ой π2.
Рис.35.
Одним из частных случаев повер-ти вр-ния явл-ся сфера. Она образуется вращением окр-ти вокруг ее диаметра.
Тема «Развертки поверхностей» изучается самостоятельно.
Лекция 7
7.1 Пересечение поверхностей
Линия пересечения 2-х поверхностей – это линия, каждая точка которой принадлежит одновременно обеим поверхностям. Строится она, в общем случае, методом вспомогательных секущих поверхностей (чаще, плоскостей) или, иначе, методом посредников. В качестве посредников применяются пл-ти уровня, пл-ти общего положения, сферические поверхности и т.д. Это зависит от конкретных условий задачи.
Решение упрощается, если обе поверхности или хотя бы одна из них занимает частное положение в пространстве, т.е. являются проецирующими. В этом случае одна из пр-ий линии пересечения (ЛП) уже имеется на проецирующей поверхности, и задача сводится к построению недостающей пр-ии линии пересечения (лп).
7.2 Свойство проецирующей поверхности:
Е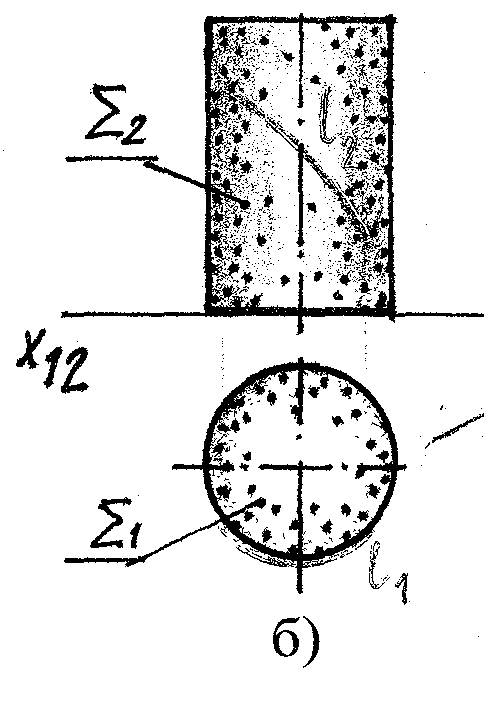
сли
одна из пр-ий линии, принадлежит
проецирующей поверхности, то другая
проекция линии совпадает со очерком
этой поверхности.
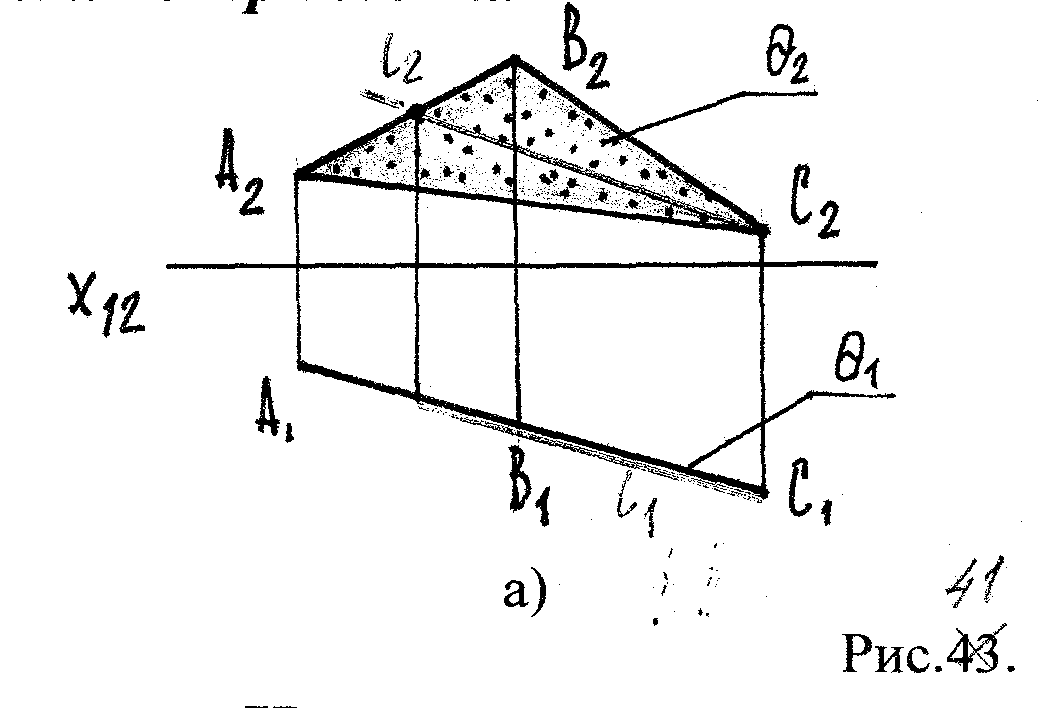
а) б)
Рис.36.
7.2 Частный случай пересечения поверхностей
Одна из пересекающихся поверхностей – проецирующая.
В этом случае одна пр-ия ЛП на чертеже уже присутствует, а 2-ая строится из условия принадлежности этой линии 2-ой пересекающейся поверхности.
Задача 1. Построить лп пл-ти общего положения Σ , заданной Δ-ком АВС с горизонтально проецирующей плоскостью Г.
И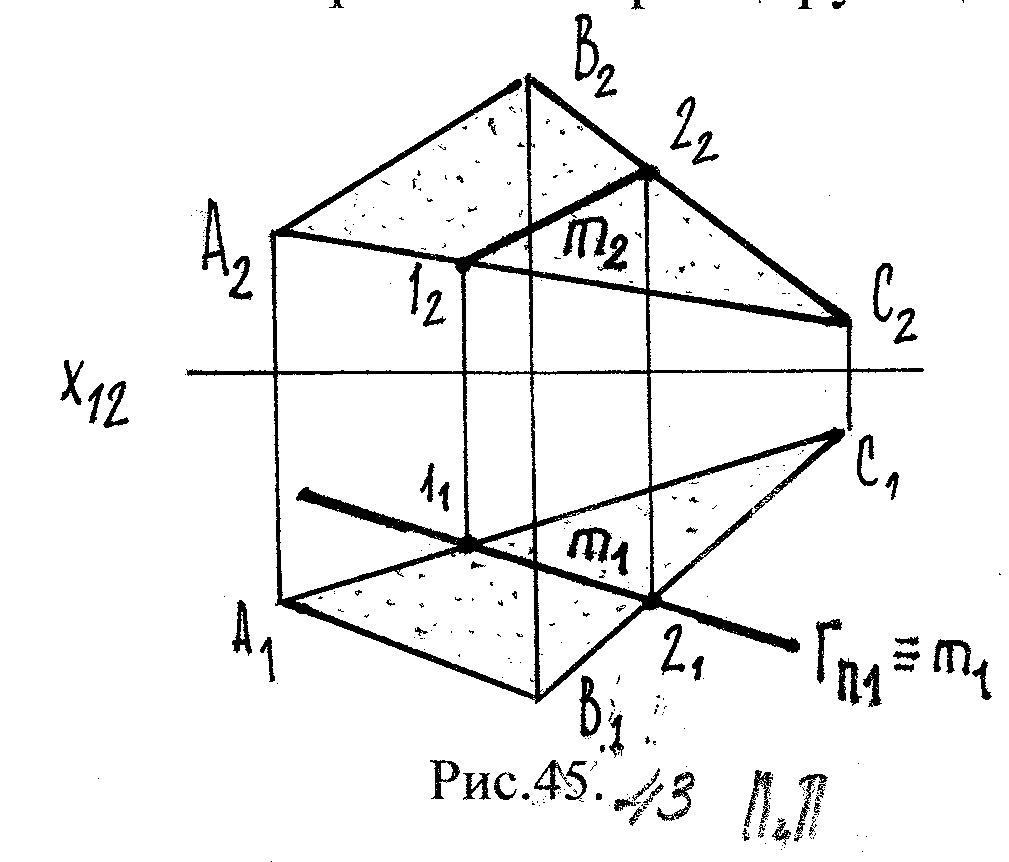
сходя
из свойства проеци-
рующей поверхности, одна
пр-ия m совпадает со следом
проецирующей пл-ти:
Г π1 m1 ≡ Гπ1
Рис.37.
Задача 2. Построить ЛП пирамиды Г с фронтально- проецирующей пл-тью Σ.
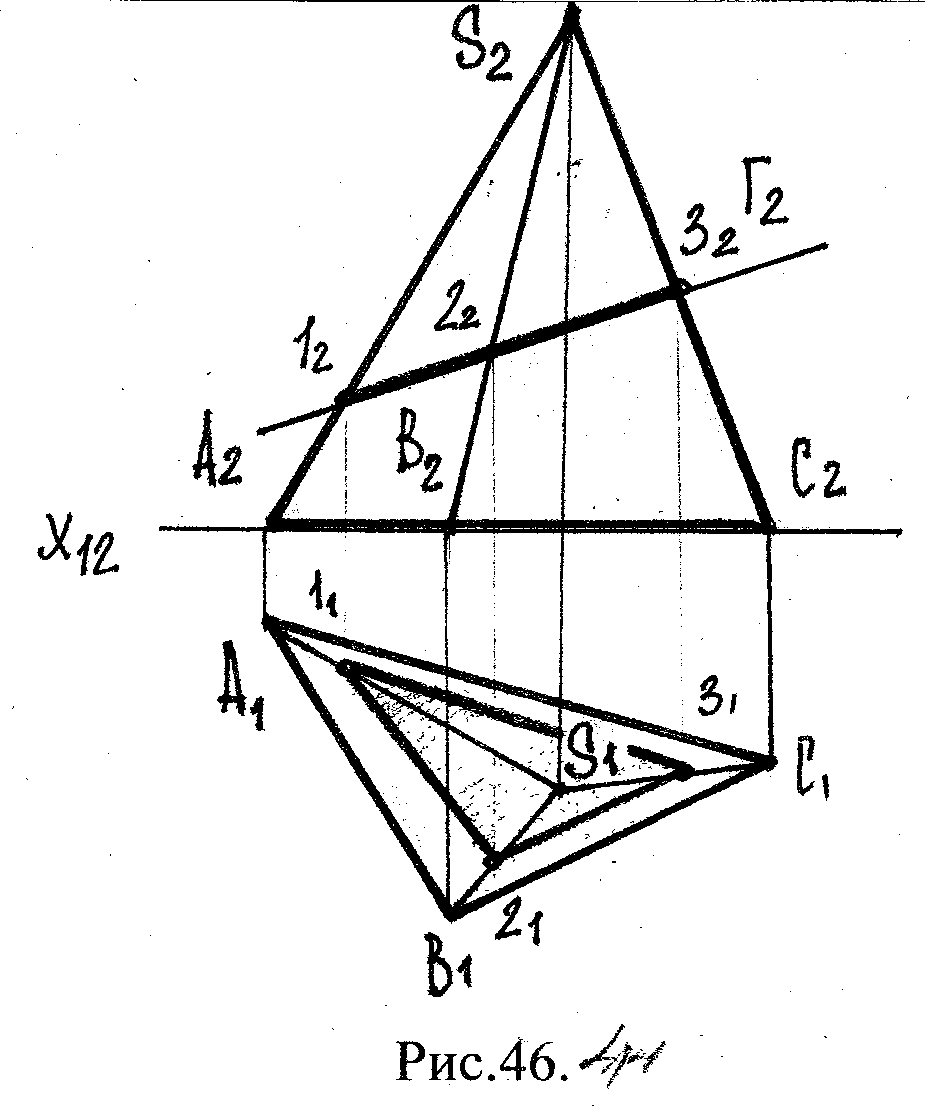Решение:
Г ∩ Σ;
Γ π2;
1-2-3 – линия пересечения
(треуг-ик) в простр-ве;
12-22-32 – прямая ≡ Г2 на черт.
Рис.38.
Задача 3. Построить ЛП конуса проецирующими пл-ми.
Линии, образующиеся при пересечении прямого кругового конуса различными проецирующими плоскостями, называются коническими сечениями.
Возможны 5 сечений конуса:
а) окружность (пл-ть Г оси i и || основанию);
m2 – линия, m2 ≡ Гπ2; m1 – окружность
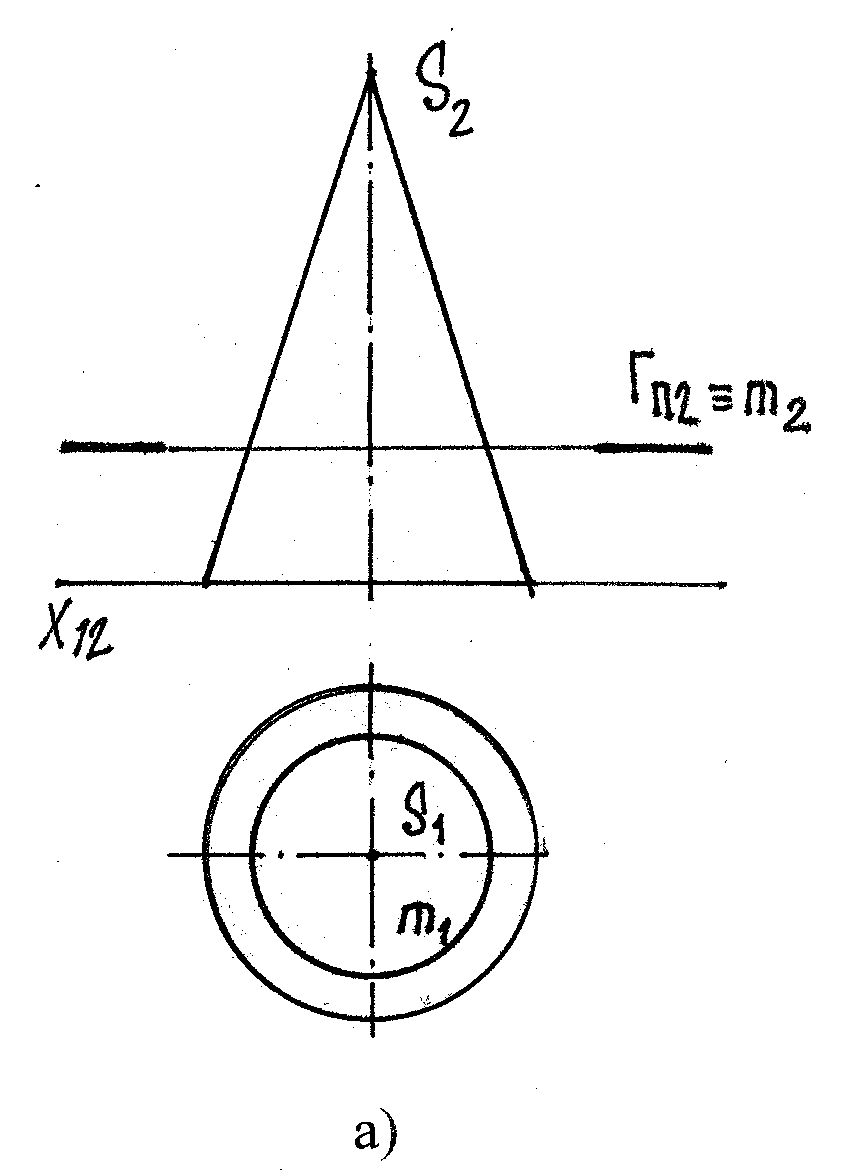
а)
б) эллипс (пл-ть Г ∩ось i) в) парабола (пл-ть || одной обр-ей)
m2 – линия, m2 ≡ Гπ2 m2 – линия, m2 ≡ Гπ2
m1 – эллипс m1 - парабола
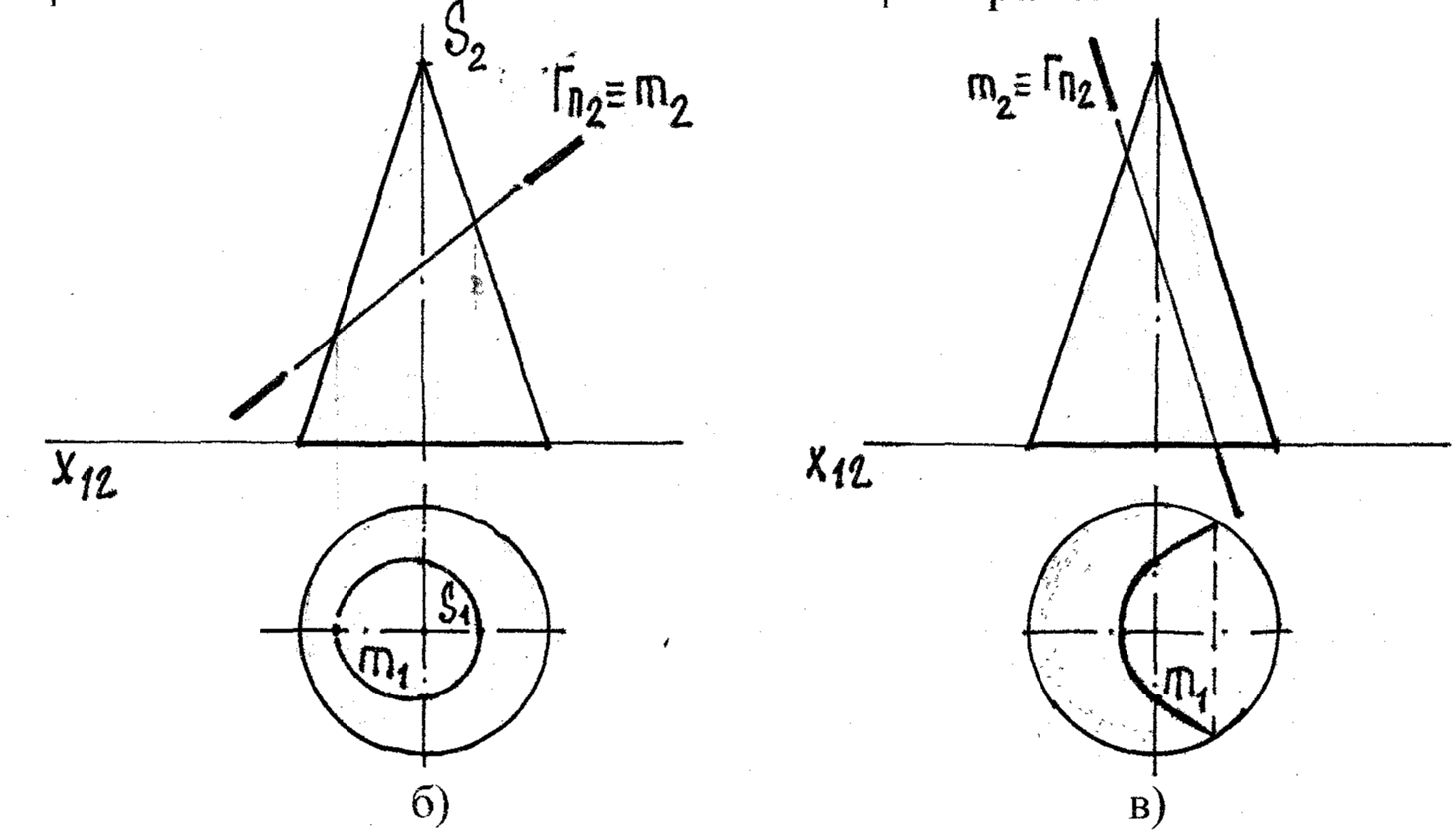
б) в)
г) гипербола д) образующая
(пл-ть Г || двум обр-щим, (пл-ть Г S (проходит
т.е. || оси конуса) через вершину)
m2 – линия, m2 ≡ Гπ2
m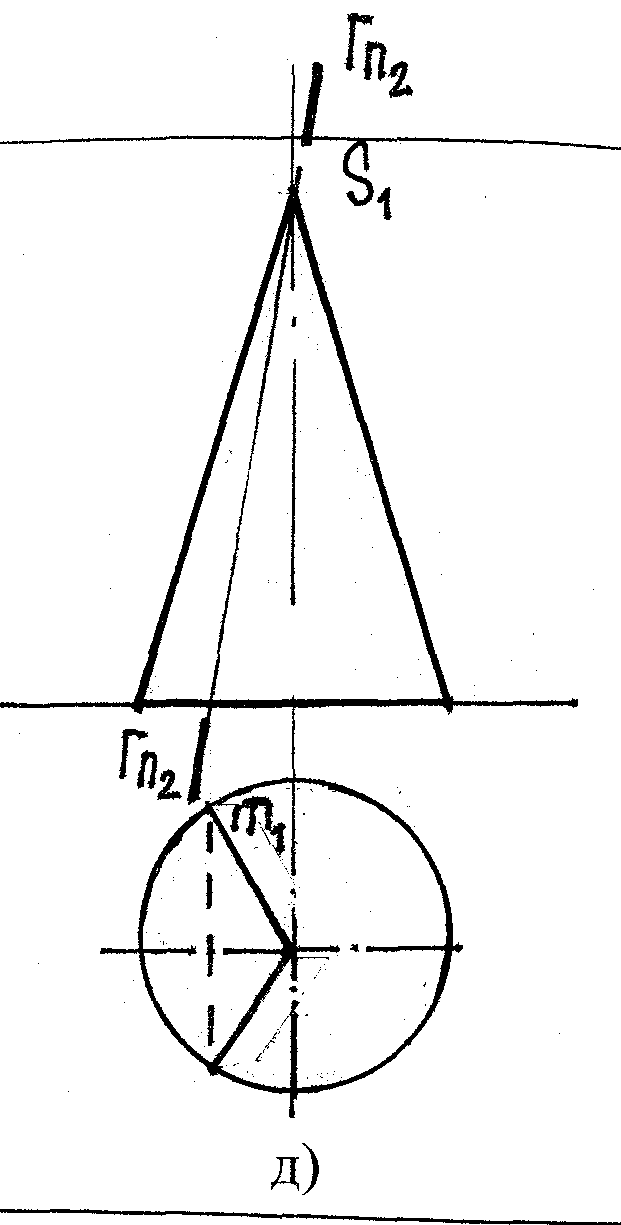
1
– гипербола
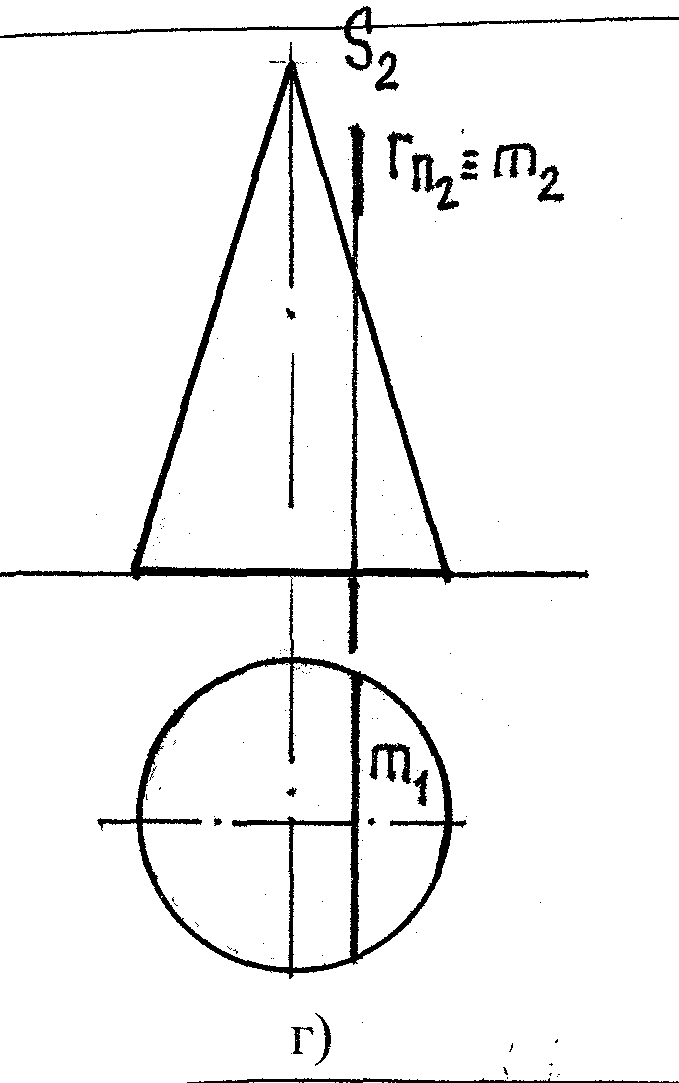
г) д)
Рис.39.