Лекция 6

6.1 Поверхности

(призма, цилиндр, пирамида, конус, сфера)

Существует множество способов образования поверхностей, мы используем кинематический способ, т.е. поверхности рассматриваются как непрерывное движение линии в пространстве по определенному закону. Линия, которая движется в пространстве и образует поверхность, называется образующей, а линия, по которой движется образующая – направляющей.

Σ – образов-ная поверхность

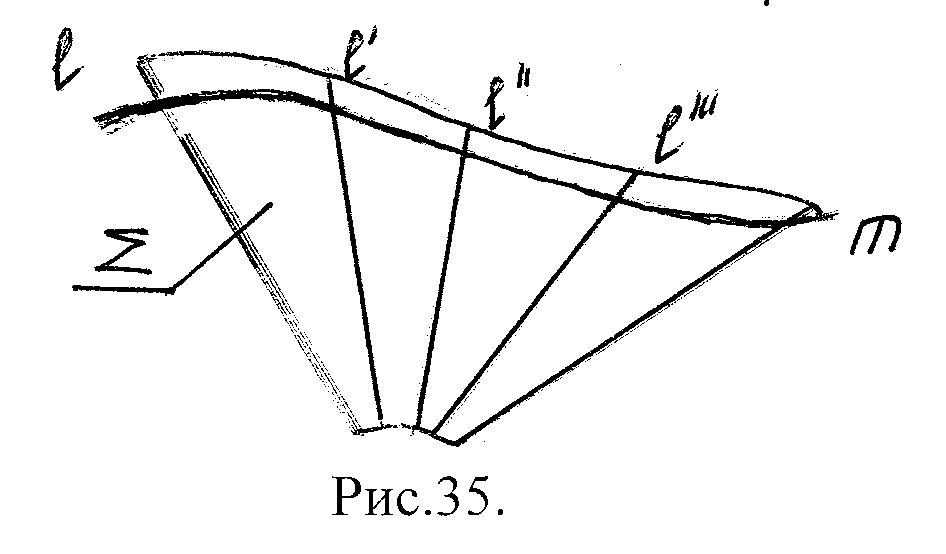
Рис.30. ℓ – образующая

m – направляющая

На чертеже любая поверхность задается определителем – совокупностью условий и геометрических элементов. Определитель записывается в символической форме:

Σ ( l, m ), где l – геометрический элемент, который движется в пространстве, m – условие.

Т.е. для изображения пов-ти необходимо иметь данные, позволяющие построить непрерывный каркас. Каркасом пов-ти наз-ся множество линий, заполняющих пов-ть.

Также на чертеже для наглядности строится очерк поверхности – это пр-ия линии контура поверхности на плоскости проекций. Очерк пов-ти отделяет видимую часть пов-ти от скрытой.

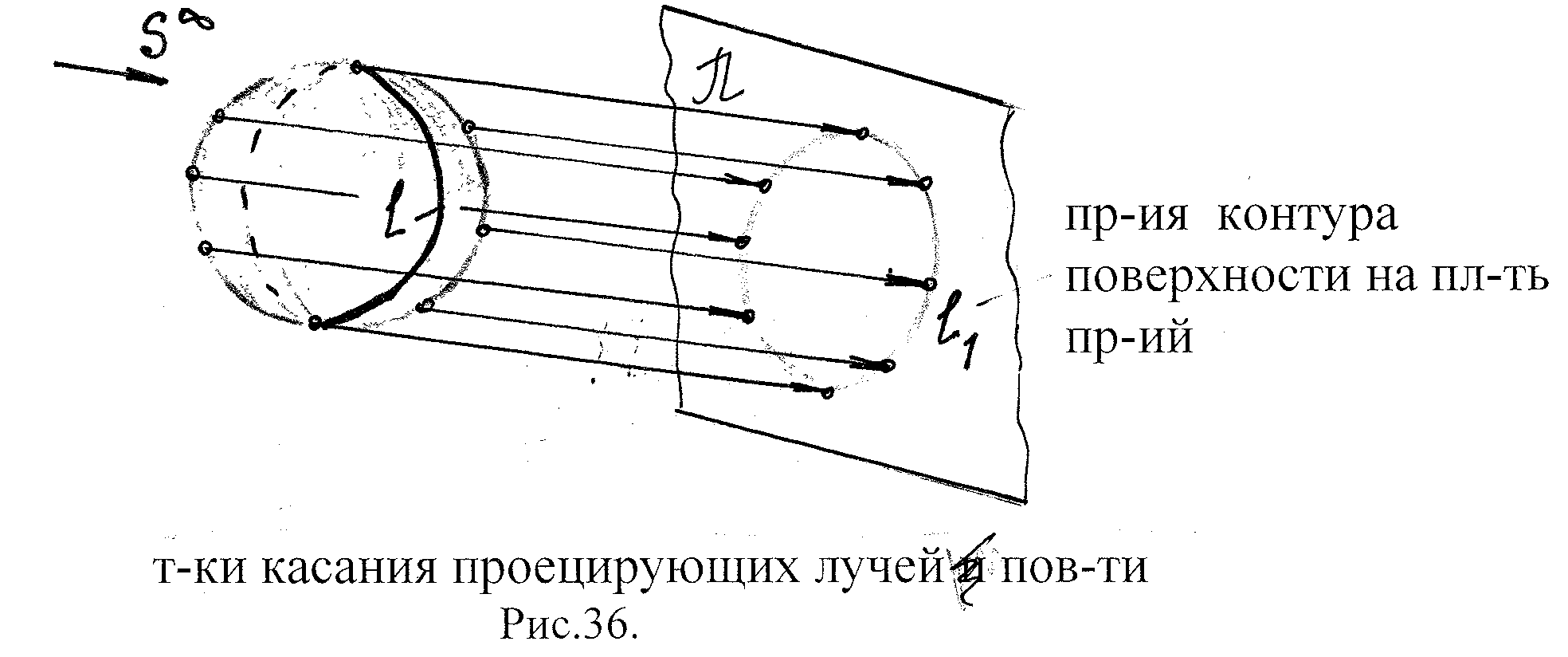
Рис. 31.

Условно поверхности разделены на 5 групп:

1. линейчатые поверхности;

2. винтовые поверхности;

3. поверхности вращения;

4. циклические поверхности;

5. графические поверхности (топографические).

6.2 Линейчатые поверхности

Линейчатые поверхности образуются непрерывным движением прямой по некоторой направляющей (прямая, ломаная или кривая линия).

Рассмотрим поверхности, образованные движением образующей, один конец которой проходит через неподвижную т-ку S, а второй - перемещается по направляющей m.

Определитель такой поверхности имеет вид: Σ (S, m),

где S – конечная точка, m – направляющая.

Поверхности, образующиеся в данной группе:

а) коническая поверхность, где направляющая – кривая, образуется движением прямолинейной образующей ℓ, скользящей по ней m и проходящей во всех своих положениях через одну фиксированную т-ку S (не лежащую на криволинейной направляющей), называемую вершиной конической поверхности.

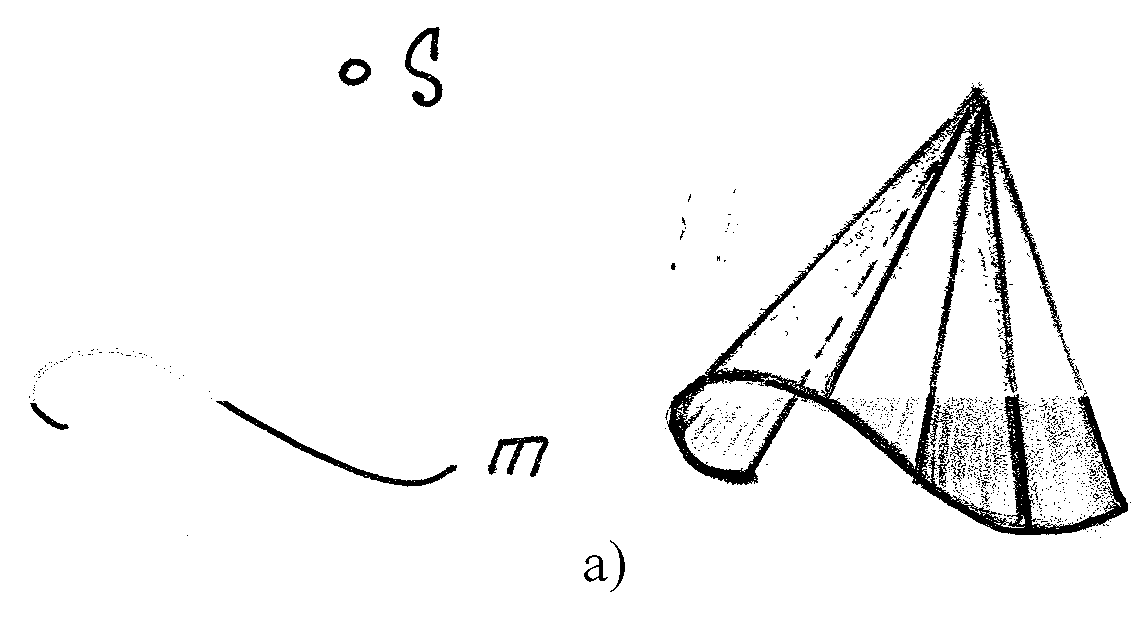
S – конечная точка

m – кривая линия

частный случай: конус, где m - окружность

б) пирамидальная поверхность образуется движением прямолинейной образующей ℓ по ломаной направляющей m и проходящей через фиксированную т-ку (вершину) S.

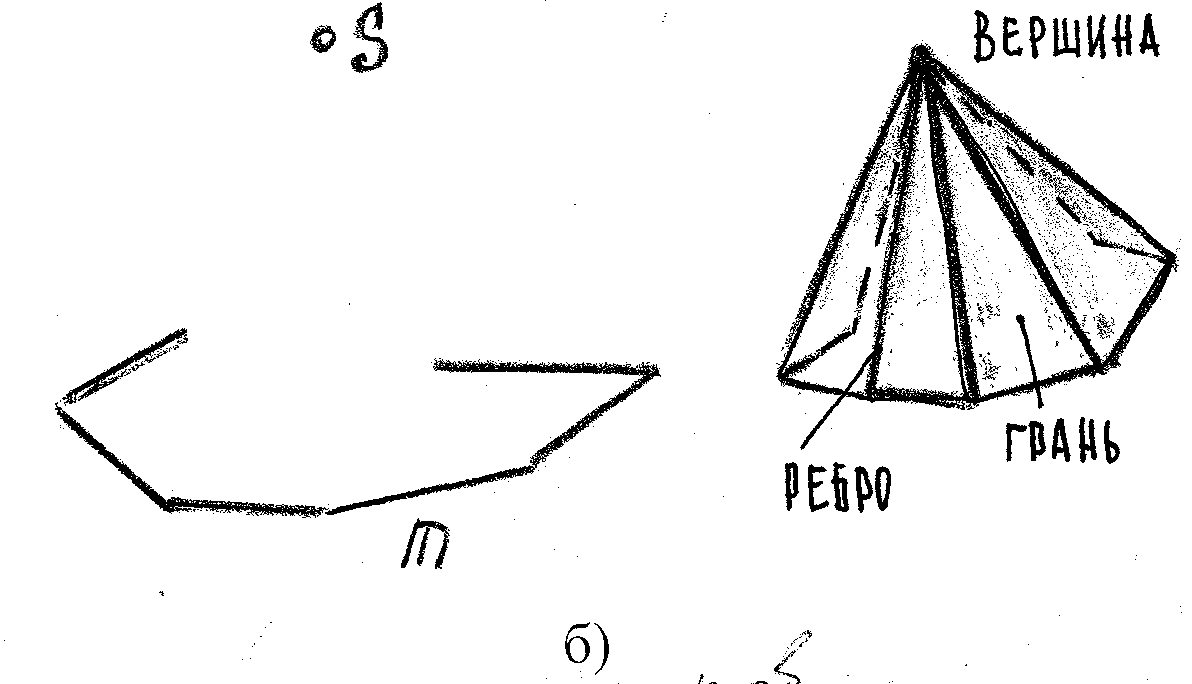
S S – конечная точка;

M m – ломаная линия

частный случай: пирамида, где m – правильный многоугольник

в) цилиндрическая поверхность образуется движением прямой ℓ, имеющей постоянное направление ↑ , S бесконечно удалена, т.е. все образующие двигаются относительно друг-друга параллельно.

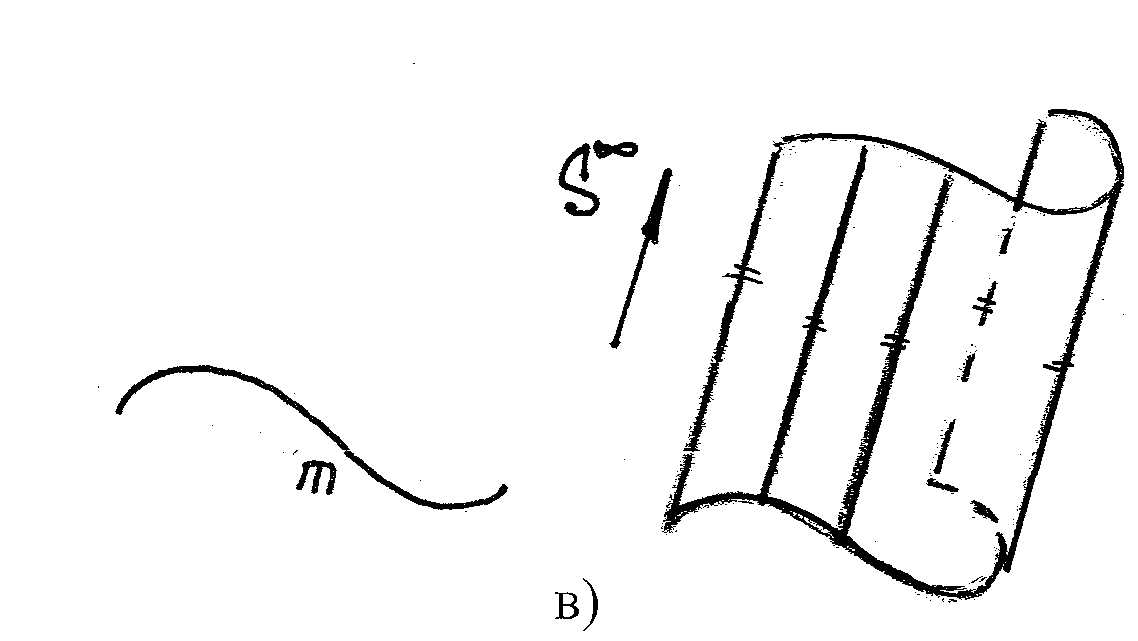S^∞–бескон.удаленная точка

m – кривая линия

частный случай: цилиндр,

где m – окружность,

i – ось вращения

г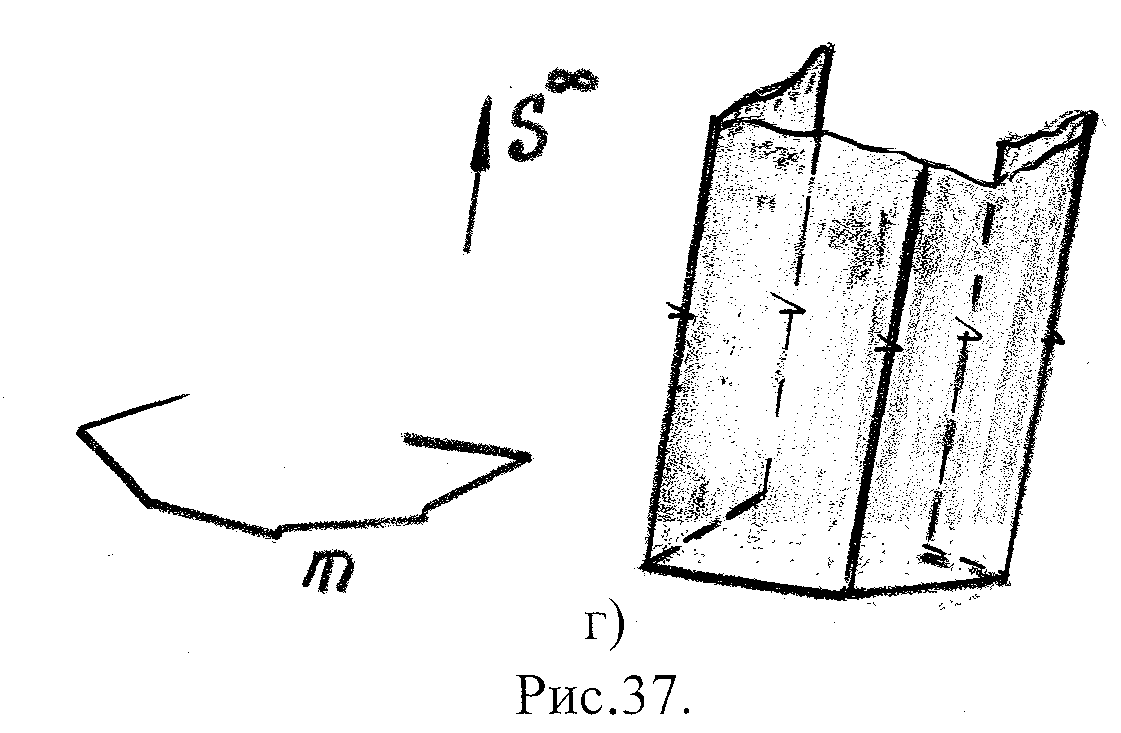 ) призматическая поверхность образуется движением прямолинейной образуюей по некоторой ломаной направляющей, при этом S бесконечно удалена.

S^∞ – бесконечно удаленная точка

m – ломаная линия

Рис.32. частный случай: призма,

где m - ломаная

Рассмотрим задачу.

Задача 1. По заданному определителю построить каркас и очерк поверхности. Построить недостающую пр-ию точки А, принадлежащую данной поверхности.

Решение:

Итак, поверхность задана определителем Σ (S, m), S - конечная точка, проекция направляющей – ломаная линия, следовательно, это пирамидальная поверхность.

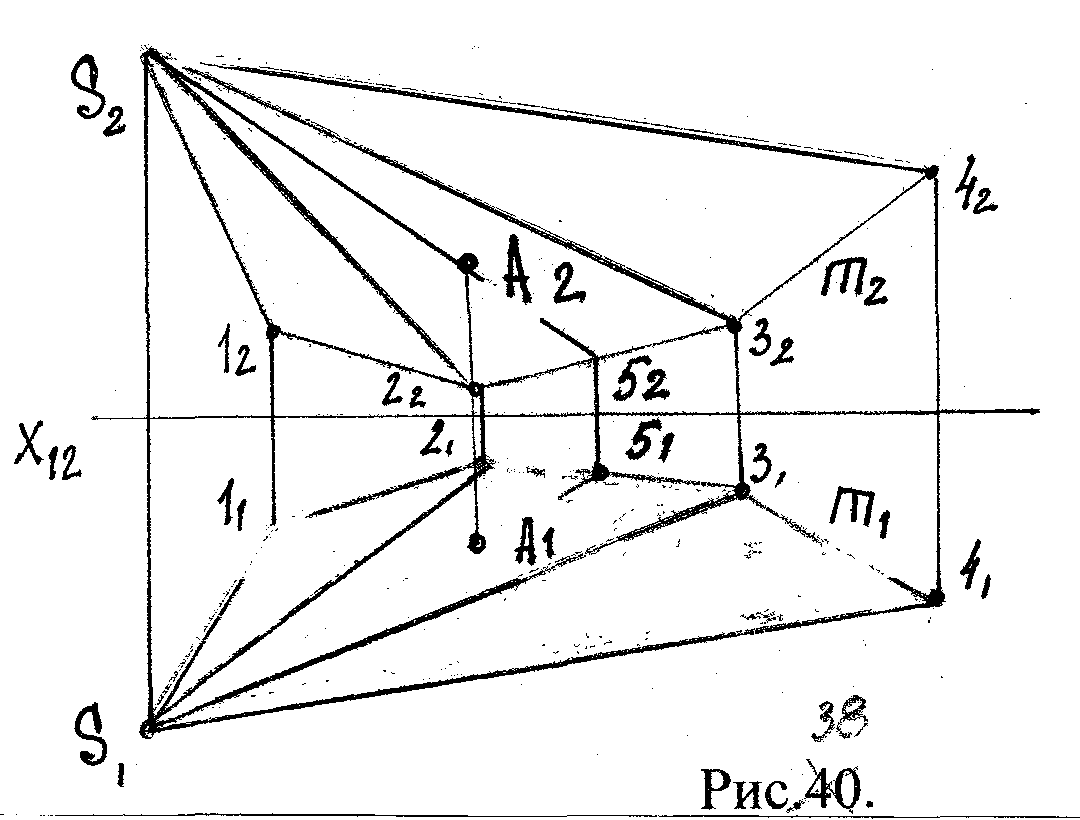
Рис.33.