4.1 Перемена плоскостей проекций

Сущность способа заключается в том, что положение геометрического образа остается неизменным, а изменяется положение плоскостей проекций. Новая пл-ть пр-ий должна быть -на неподвижной плоскости проекций (это обязательное условие). Причем новая пл-ть пр-ий ставится так, чтобы геометрический образ в новой системе пл-тей занимал частное положение. -сть линий связи относительно осей сохраняется. Изменение положений плоскостей проекций может осуществляется последовательно не более 2 раз.

4.1.1 Замена фронтальной плоскости проекций

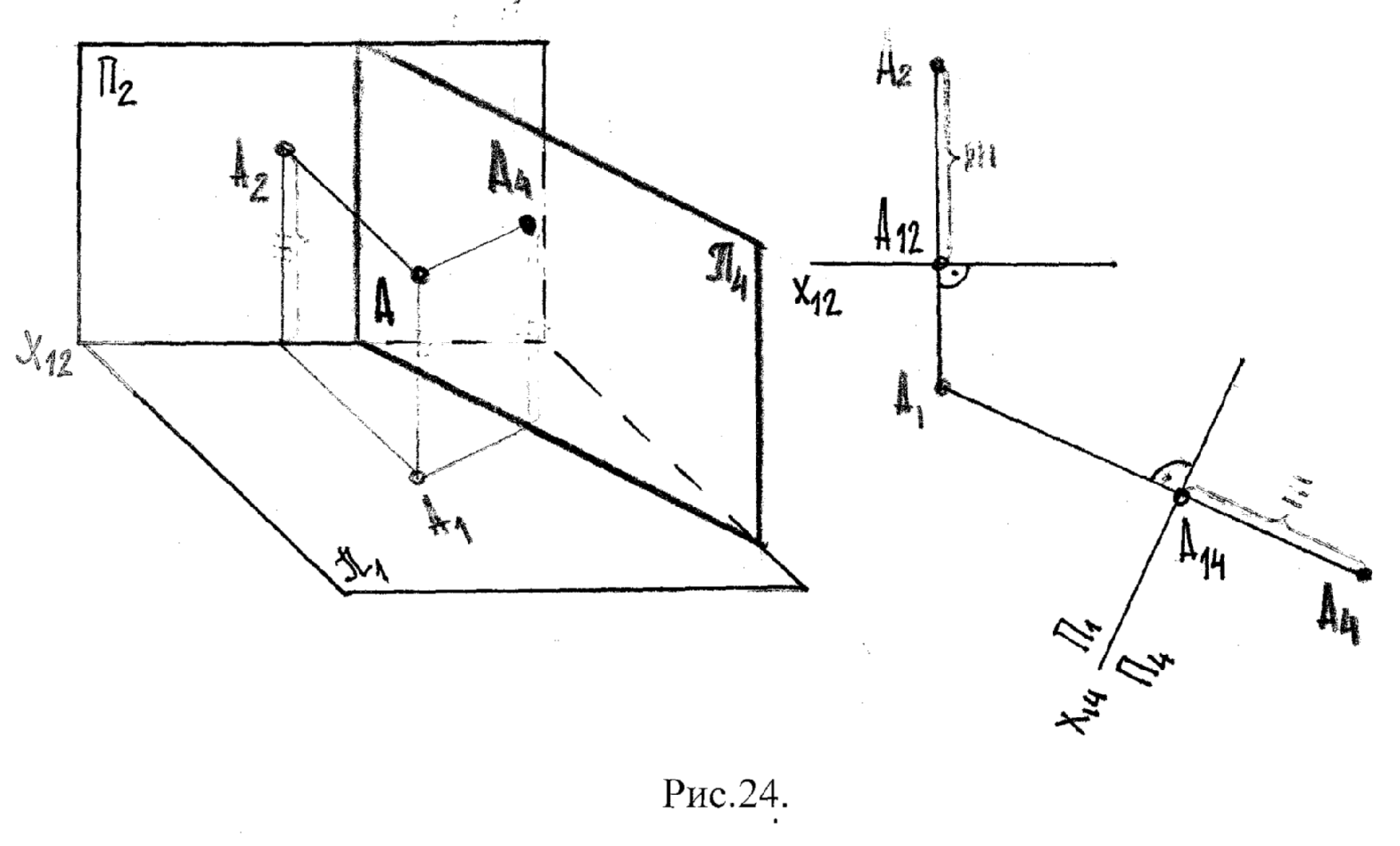
Заменим фронт. плоскость проекций π₂ на новую фронт. плос-ть π₄.

Спроецируем т.А на пл-ть π₄, которая так же как и π₂ π₁  А₄. Т.е. мы произвели замену плоскости проекций:

π₂  π₄; π₄  π₁; А₁₂–А₂ = А₁₄–А₄

π₁ π₁

На плоском чертеже из точки А₁ -но к оси Х₁₄ проводим линию связи для нахождения А₄.

4.1.2 Замена горизонтальной плоскости проекций.

Принцип замены горизонтальной плоскости проекций такой-же, как и в предыдущем случае, с фронтальной пл-тью пр-ий.

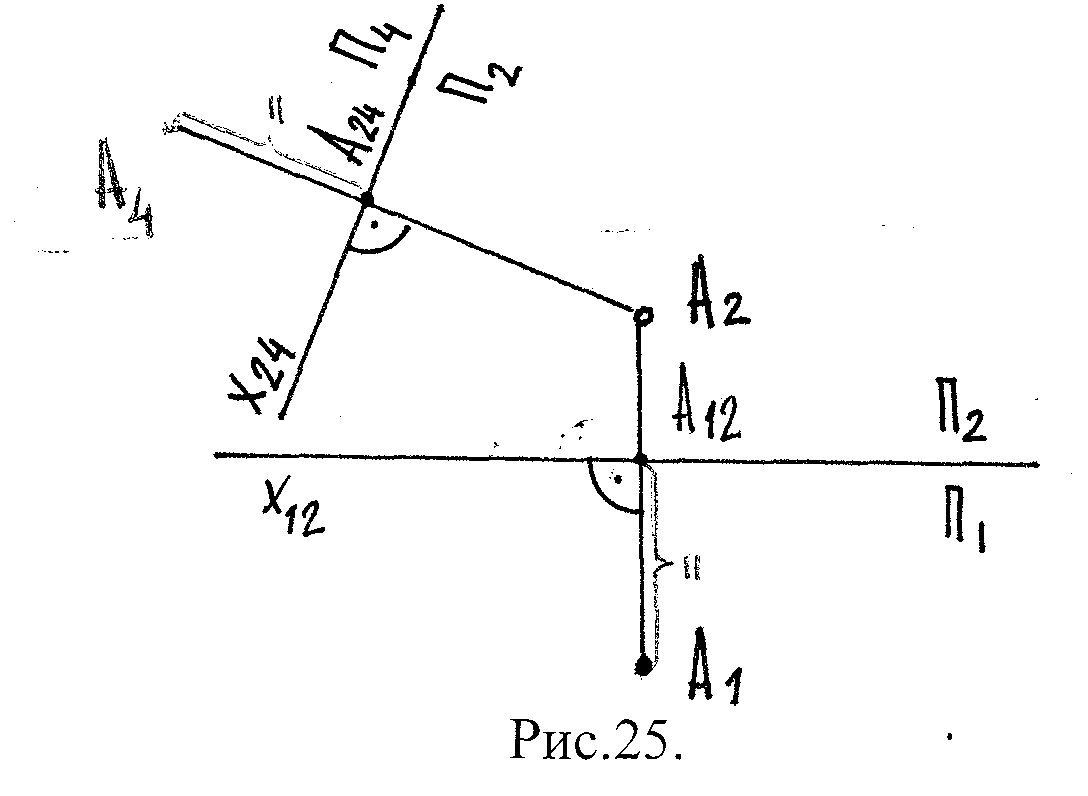π₂  π₂; π₄  π₂;

π₁ π₄

А₁₂–А₁ = А₂₄–А₄

Рассмотрим решение задач:

Задача 1. Определить НВ отрезка АВ.

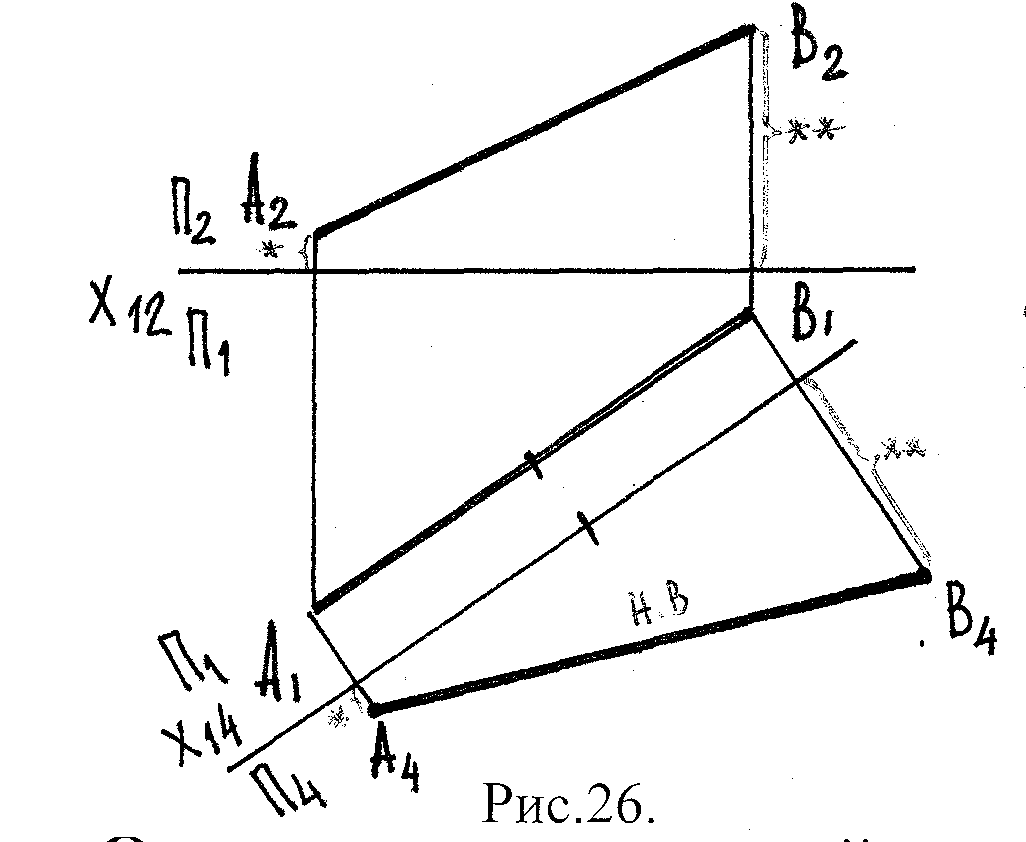Решение:

π₂  π₂;

π₁ π₄

Х₁₄ А₁В₁; АВ π_4;

А₄В₄ – н.в.

Лекция 5

5.1 Способ вращения

При решении задач способом вращения положение заданных геометрических элементов изменяют путём вращения их вокруг проецирующей оси.

Выбор оси вращения, направления вращения и угла поворота заданного геометрического элемента позволяет привести последнее в частное положение. В некоторых случаях приходится вращать дважды: сначала вокруг одной, а затем и второй оси вращения.

Базовые плоскости проекций остаются неизменными. Относительно этих плоскостей проекций меняется положение геометрического элемента. Желательно, чтобы ось вращения проходила хотя бы через одну т-ку прямой, которую необходимо повернуть.

Точка при вращении вокруг какой-либо оси описывает траекторию, представляющую собой окружность, расположенную в плоскости, -ой к оси вращения.

Сущность способа вращения:

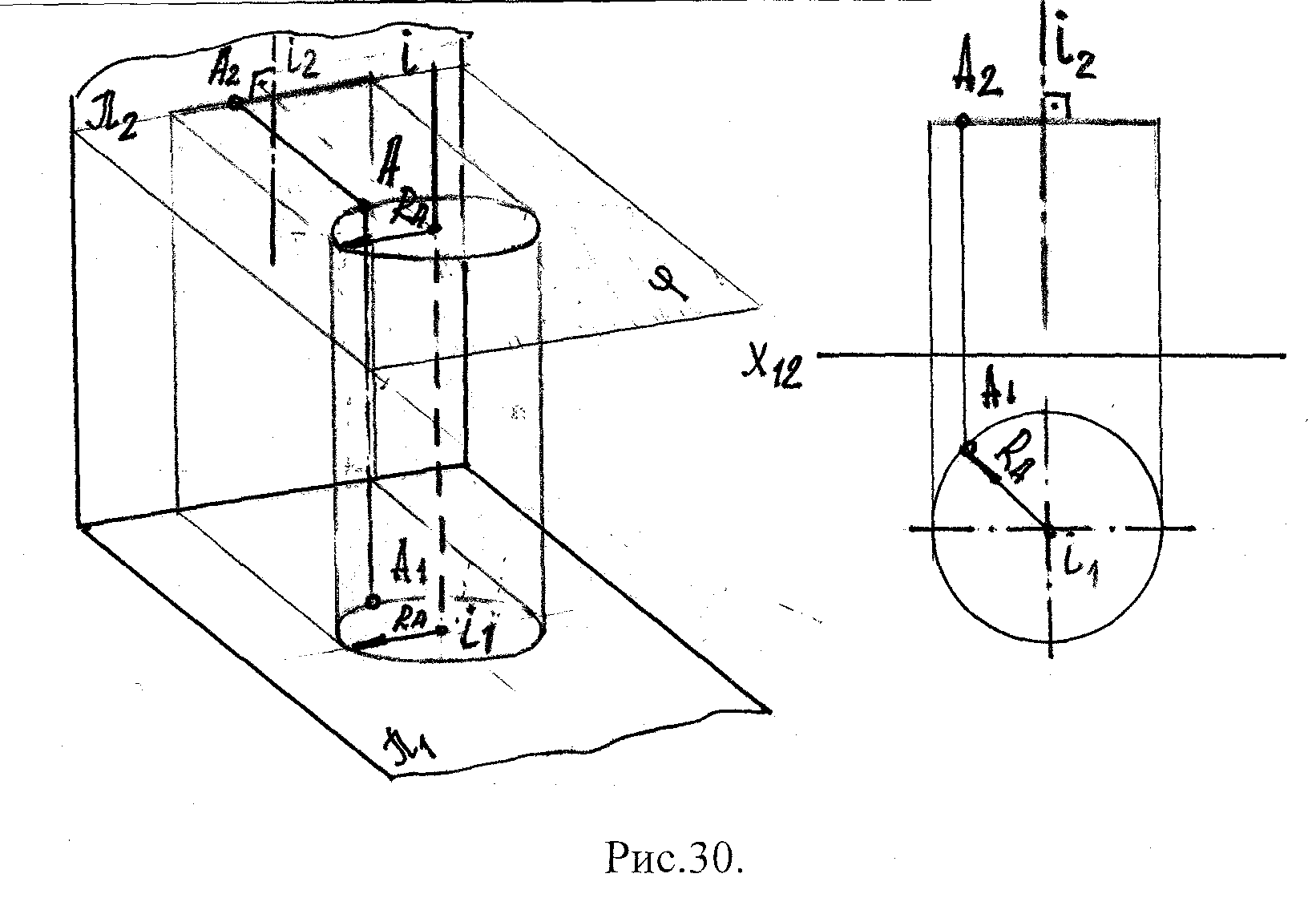
Рис.27.

Точка в пространстве вращаясь вокруг оси i, опишет окружность, плоскость которой   i. Траектория этой окружности на одну пл-ть пр-ий проецируется в виде окружности, а на 2-ую – в виде прямой, ||-ой оси Х₁₂ и -ой оси вращения i.

Р ассмотрим задачи:

Задача 1. Определить НВ отрезка АВ вращением вокруг проециру-ющей оси.

Решение:

i  π₁

Выбор оси осущ-ся так, чтобы при решении задачи было меньше построений.

В данном случае, ось i -на π₁ и проходит через т.А. т.А остается

неподв-ой , а т.В вращ-ся по окр-ти.

Рис.28.

З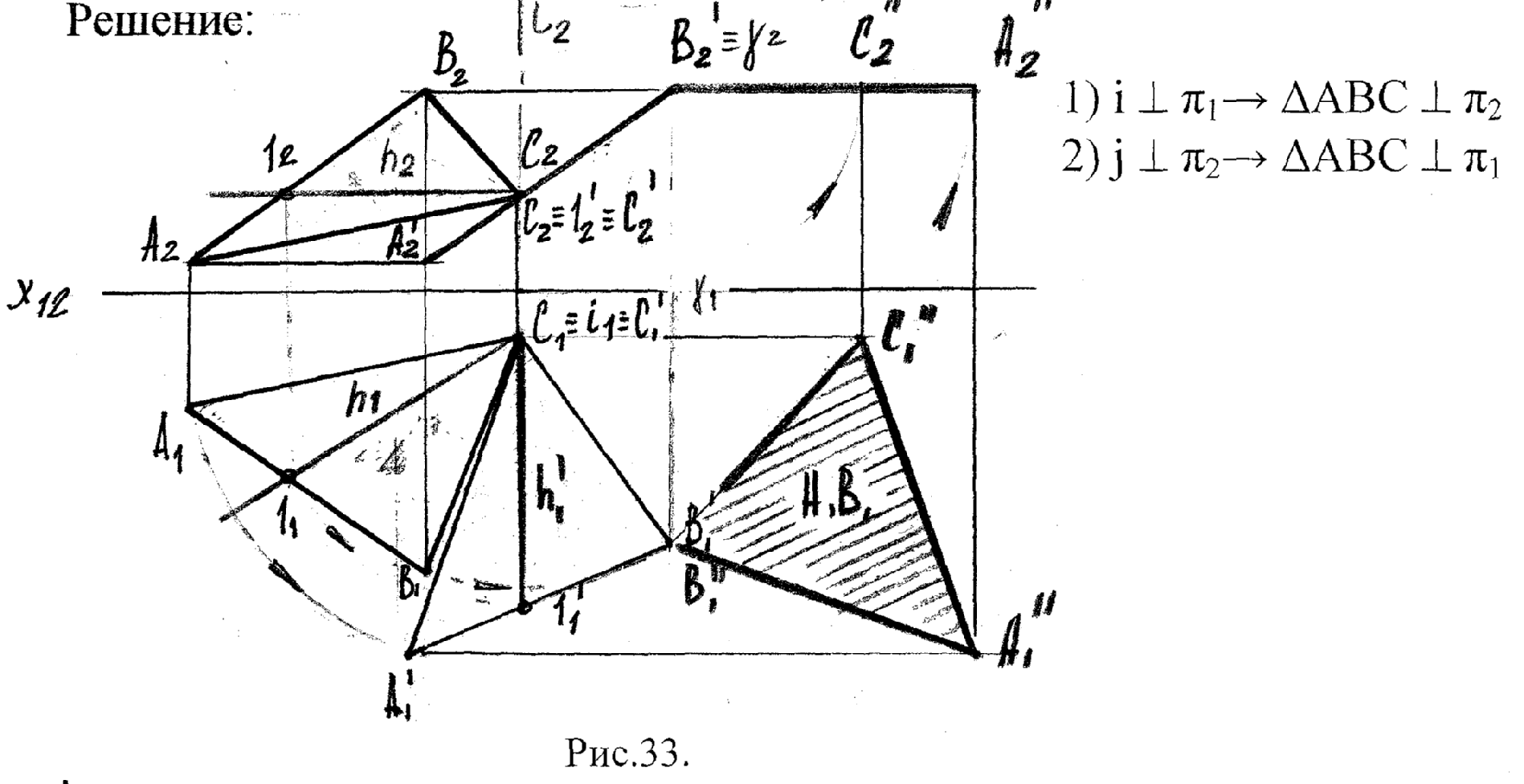 адача 2. Определить НВ Δ АВС вращением вокруг проецирующих осей.

Рис.29.