3.2 Плоскости общего положения

Это плоскость ни параллельная, ни перпендикулярная ни одной из плоскостей проекций.

3.3 Плоскости частного положения

3.3.1 Пл-ти уровня – это пл-ти, || -ые одной из плоскостей проекций, и -ые двум остальным пл-тям пр-ий (дважды проецирующие).

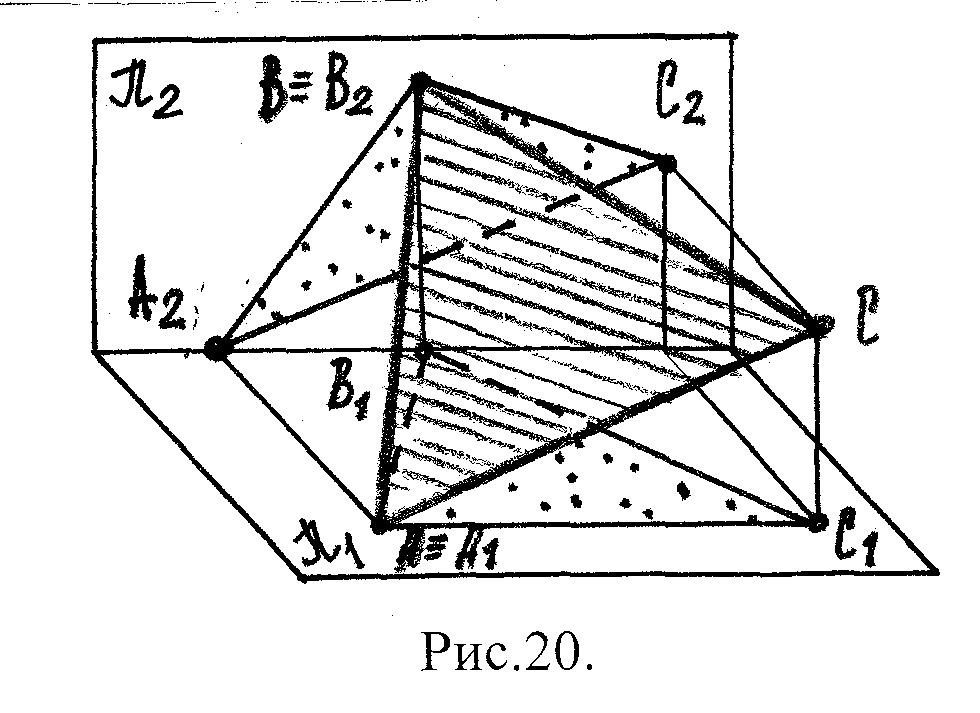
а) Плоскость горизонтального уровня - || π₁

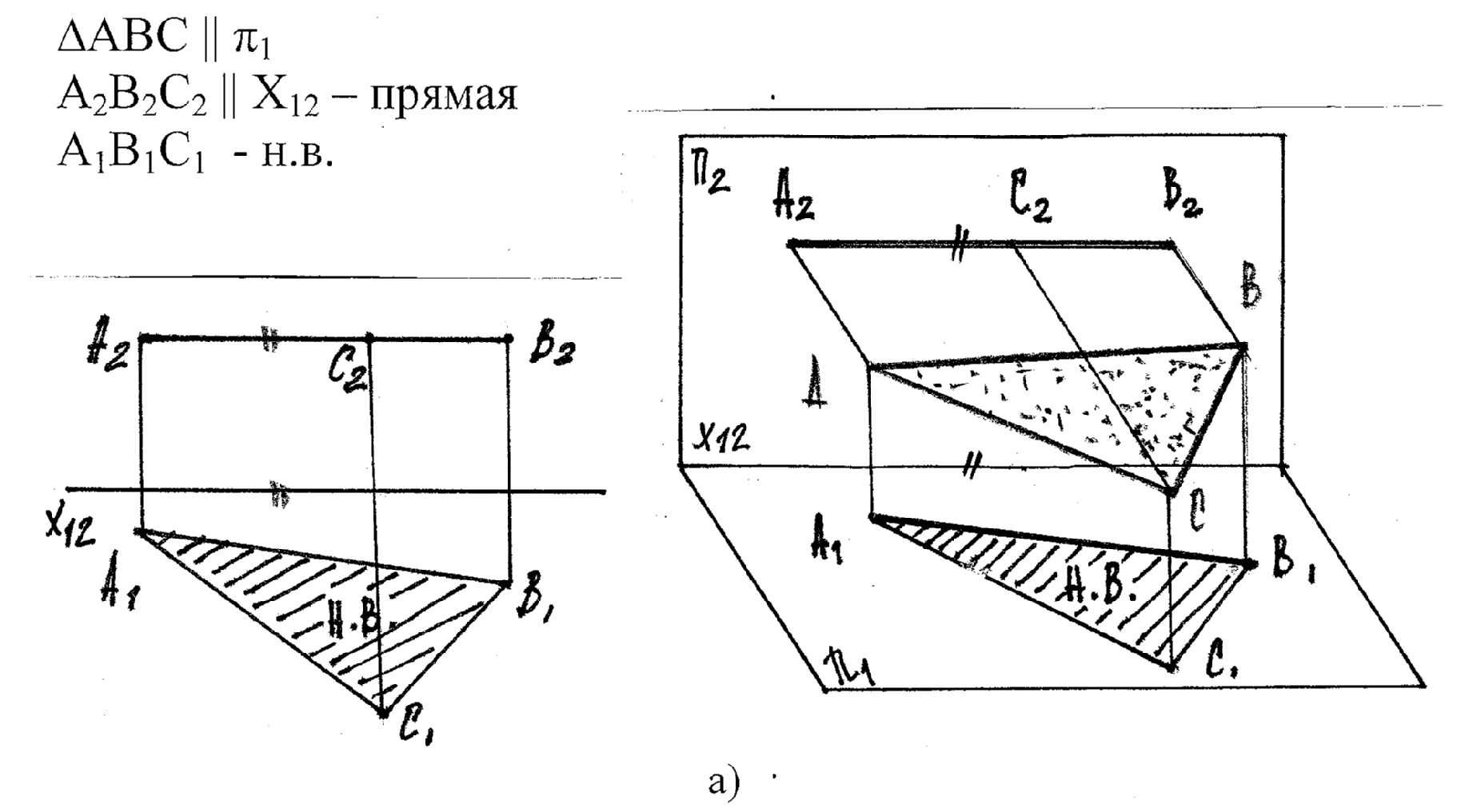
б) Плоскость фронтального уровня - || π₂

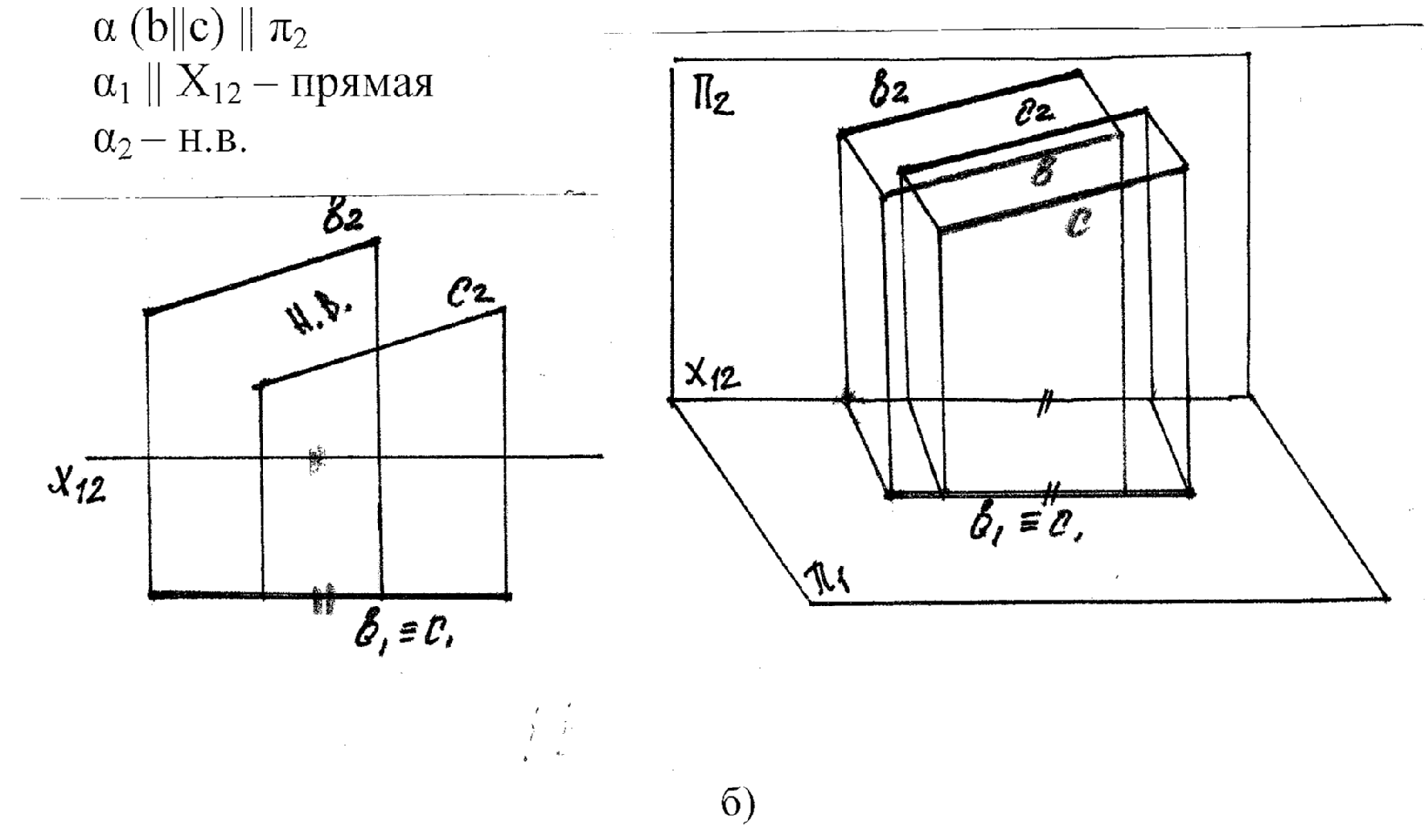
в) Плоскость профильного уровня -|| π₃ (рис.20 в)

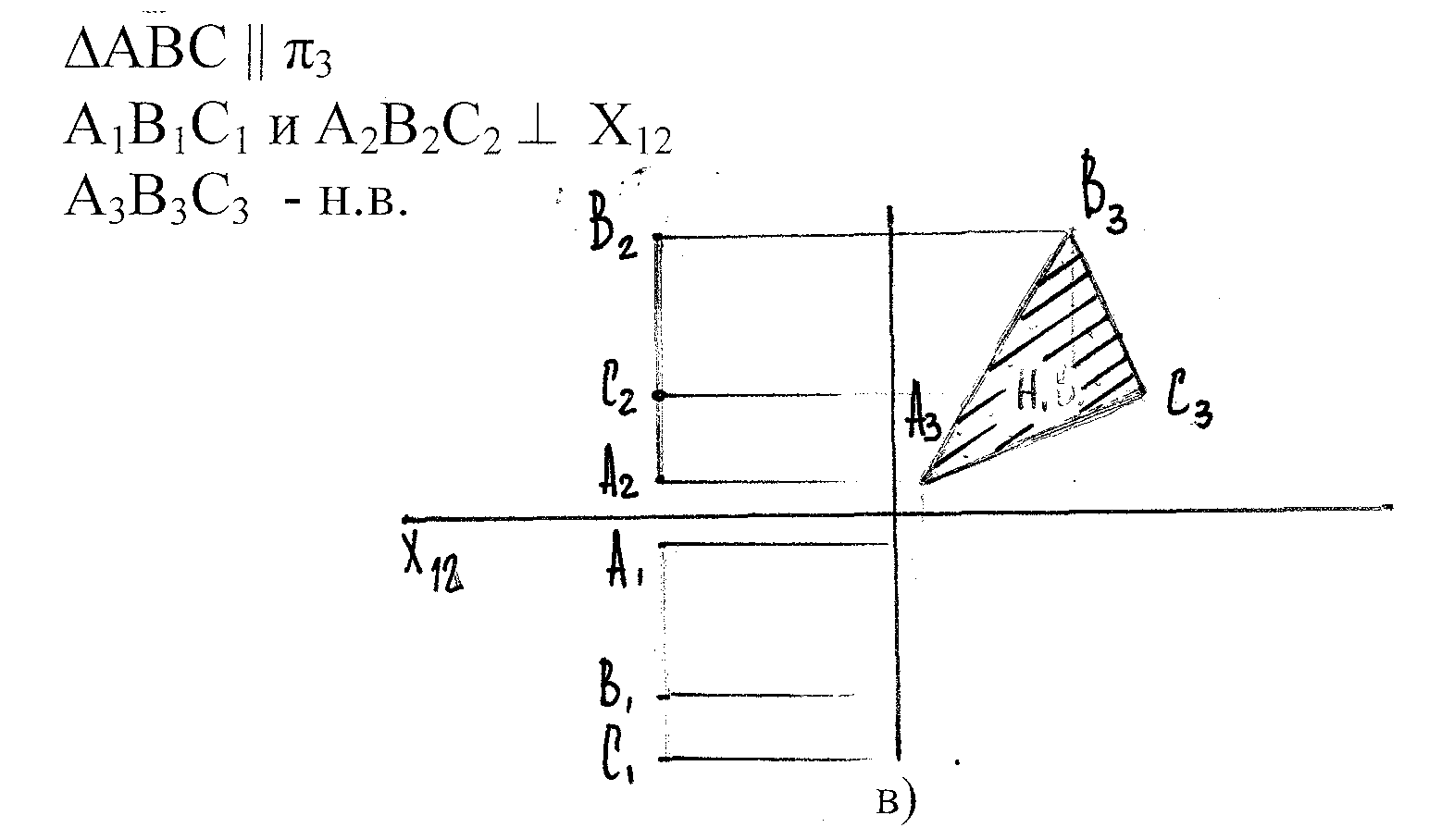
Свойство плоскостей уровня:

Прямая или фигура, лежащая в плоскости уровня проецируеся без искажения на ту пл-ть пр-ий, которой данная плоскость уровня параллельна.

3.3.2 Проецирующие плоскости – это пл-ти, -ые только одной из плоскостей проекций.

а) Горизонтально проецирующая плоскость -  π₁

Если пл-ть задана треугольником, то горизон-ая пр-ия изображается в виде отрезка.

Свойство проецирующей пл-ти:

Все плоские геометрические фигуры, принадлежащие к горизонтально-проецирующей пл-ти проецируются на горизонтальный след данной пл-ти в виде отрезка прямой.

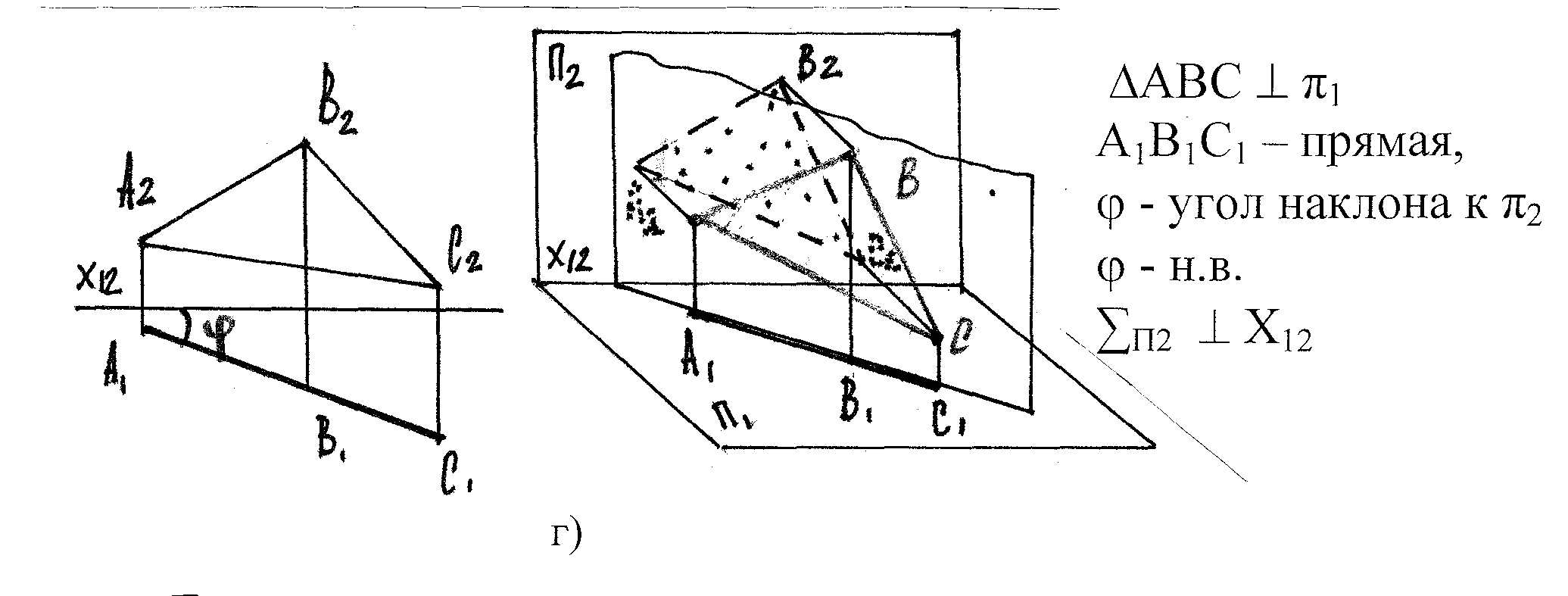
б) Фронтально проецирующая плоскость -  π₂

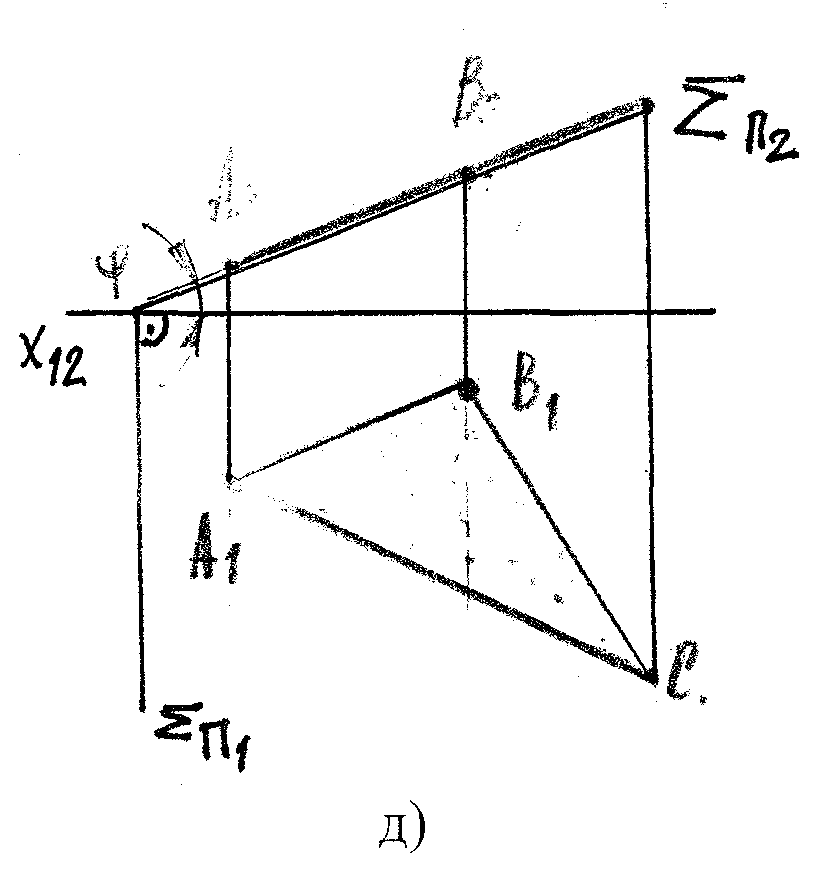
АВС  π₂

А₂В₂С₂ – прямая,

 - угол наклона к π₁

 - н.в.

∑_П1  Х₁₂

в) Профильно проецирующая плоскость -  π₃

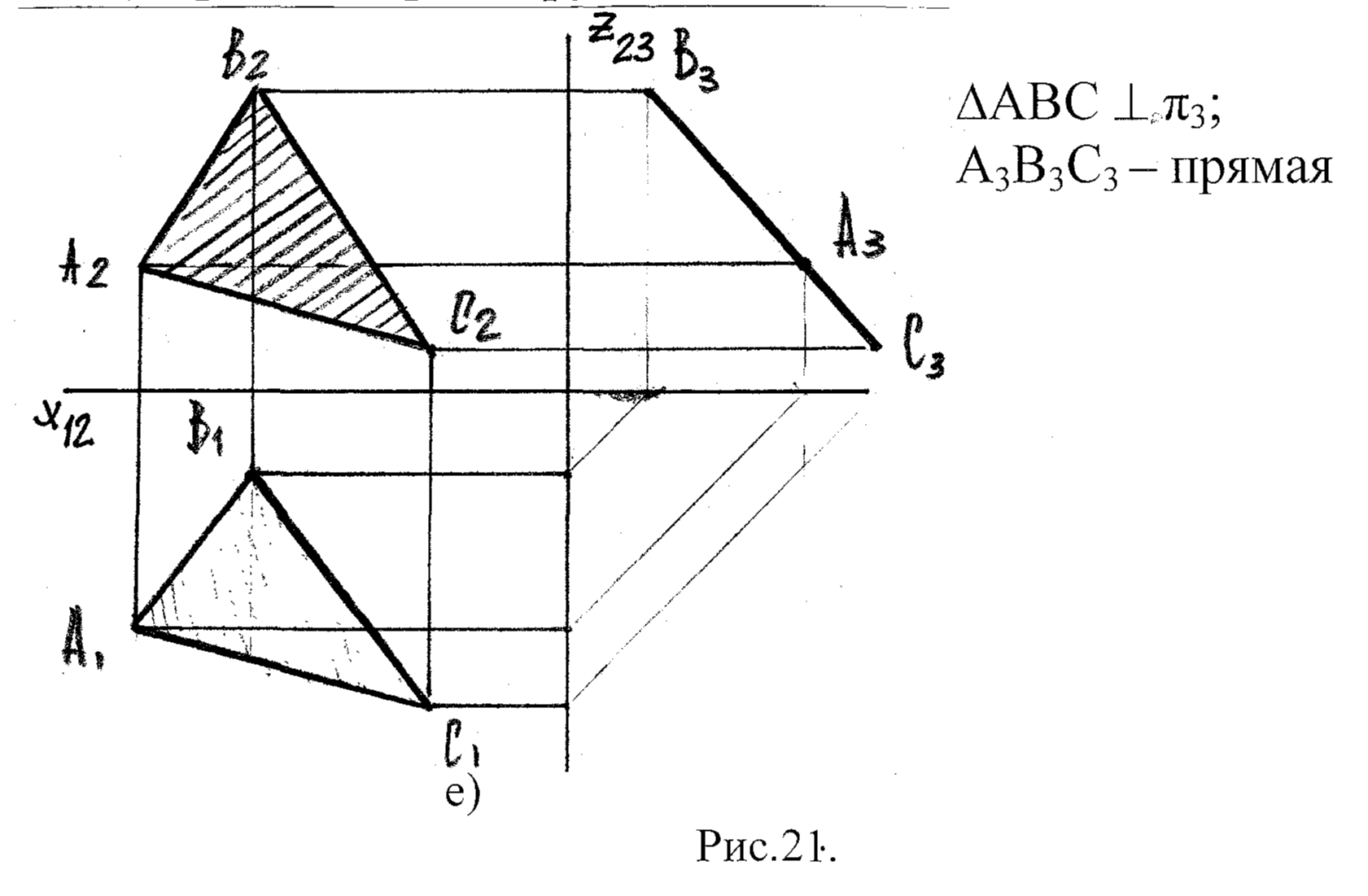
3.4 Признак принадлежности точки и прямой плоскости

Теорема 1: Точка  пл-ти, если она расположена на прямой, лежащей в данной пл-ти.

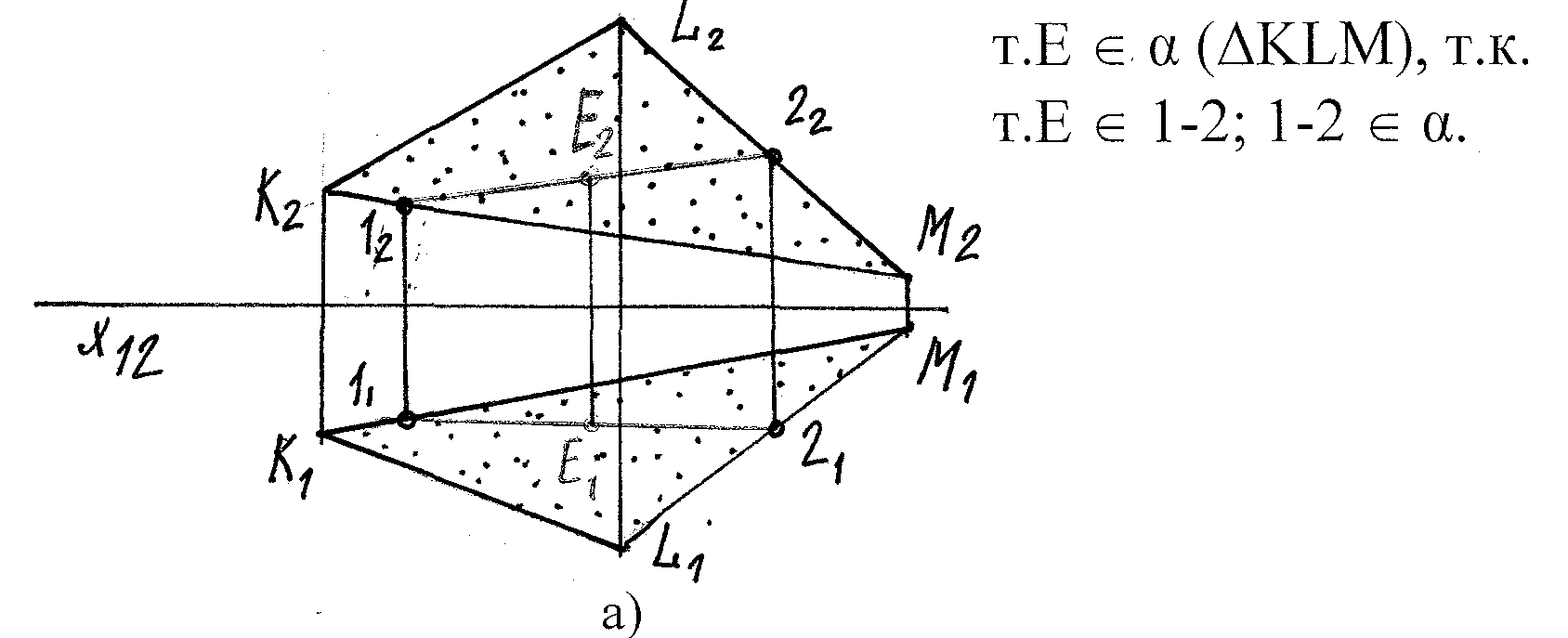
Теорема 2: Прямая  пл-ти, если она имеет с ней две общие точки.

ℓ ∩ Σ (k||e) → 1-2

3.5 Главные линии плоскости (особые)

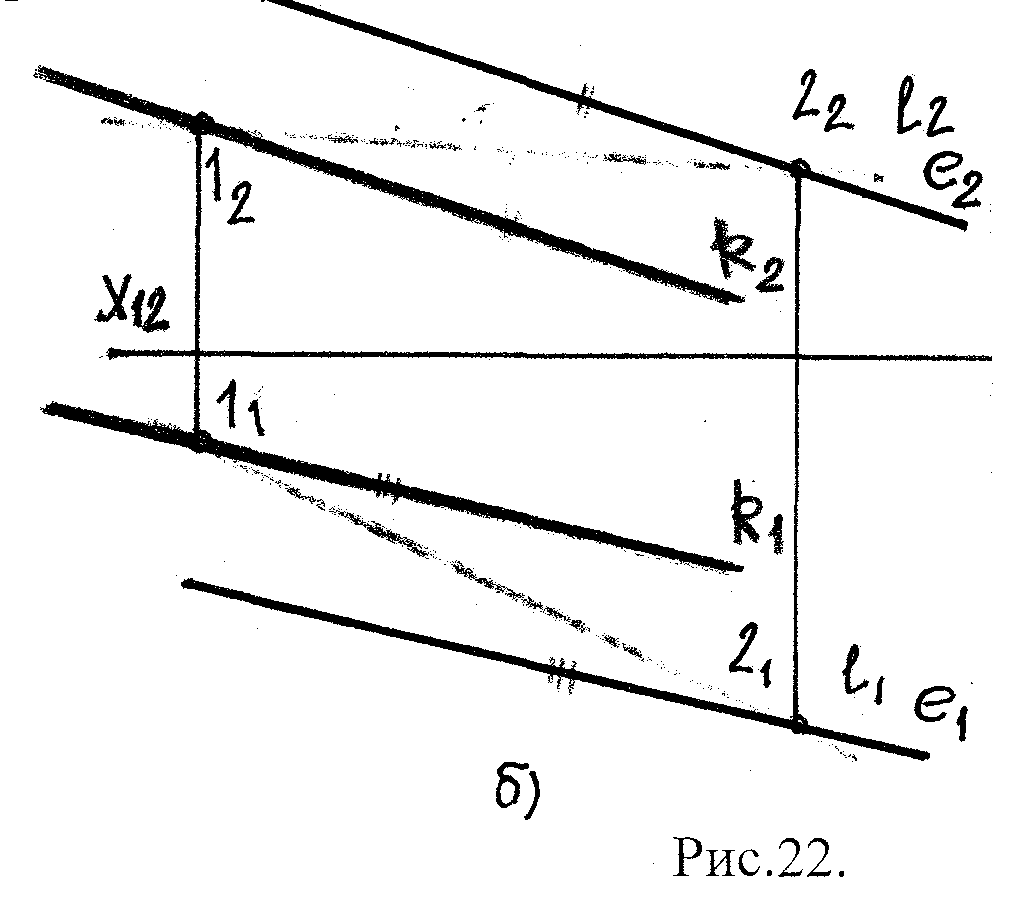
1. Горизонталь плоскости – прямая, принадлежащая заданной пл-ти и || π₁.

h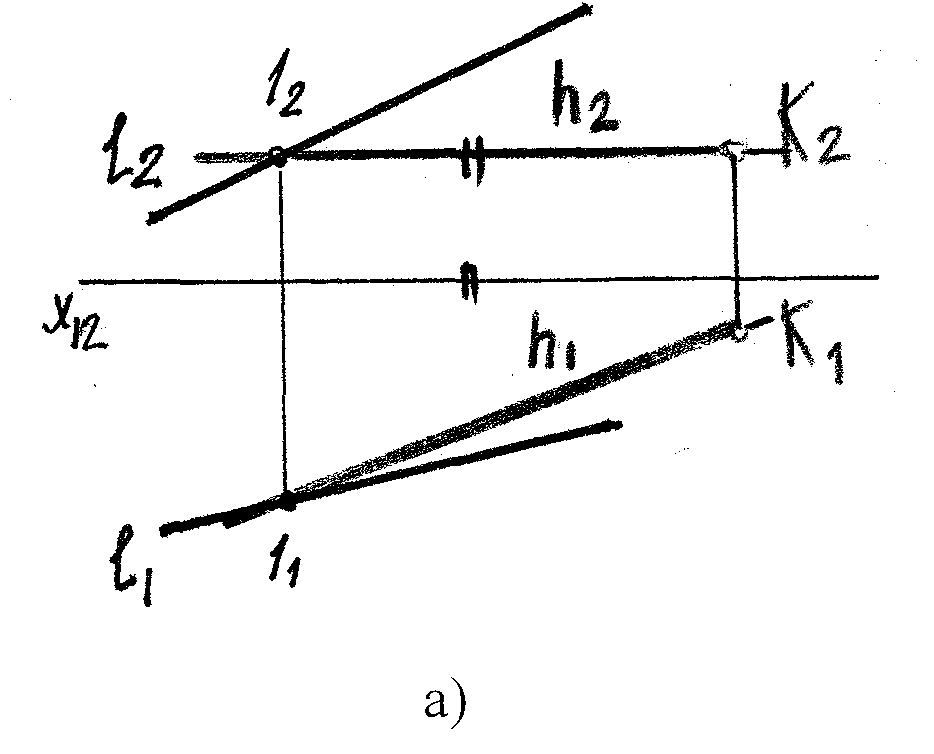 || π₁; - в простр.

h  α (ℓ; К)

h₂ || Х₁₂ – на черт.

2. Фронталь плоскости – прямая, принадлежащая заданной пл-ти и || π₂.

f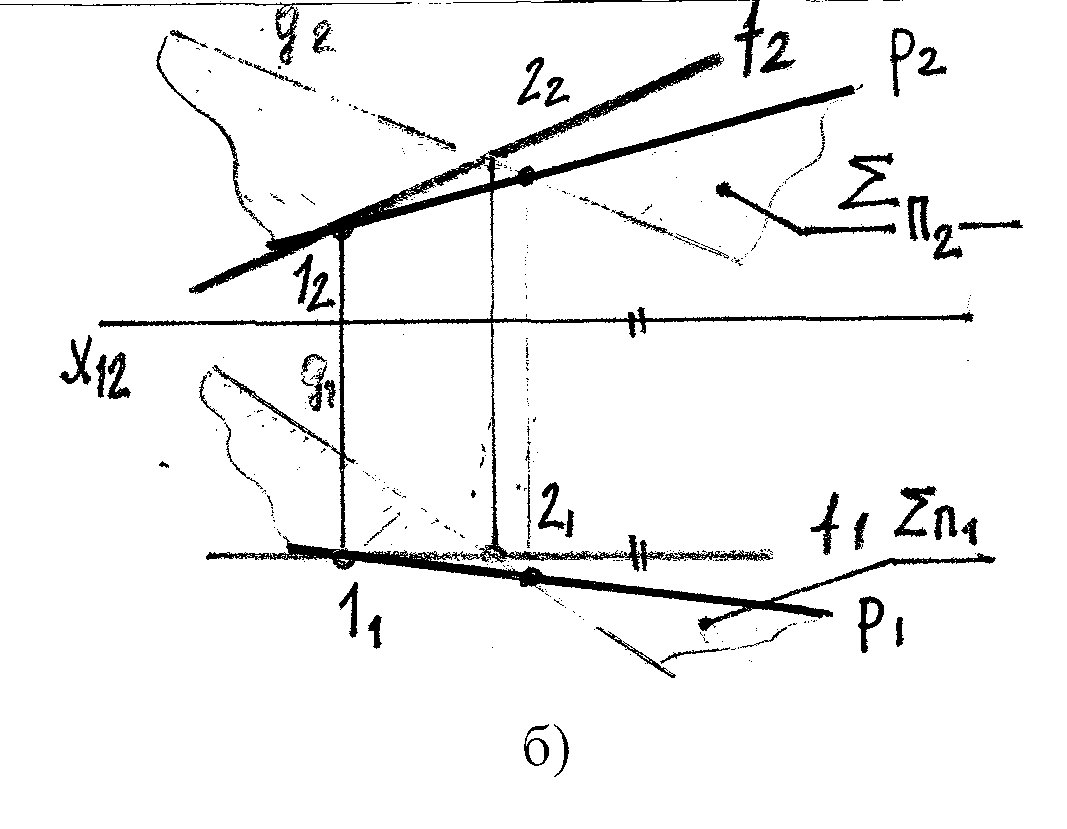 || π₂; - в простр.

f  Σ (p ∩ q)

f₁ || Х₁₂– на черт.

3. Линия наибольшего ската (ЛНС) – это прямая, лежащая в пл-ти и -ая к горизонталям плоскости. Эта линия определяет угол наклона заданной пл-ти к π₁.

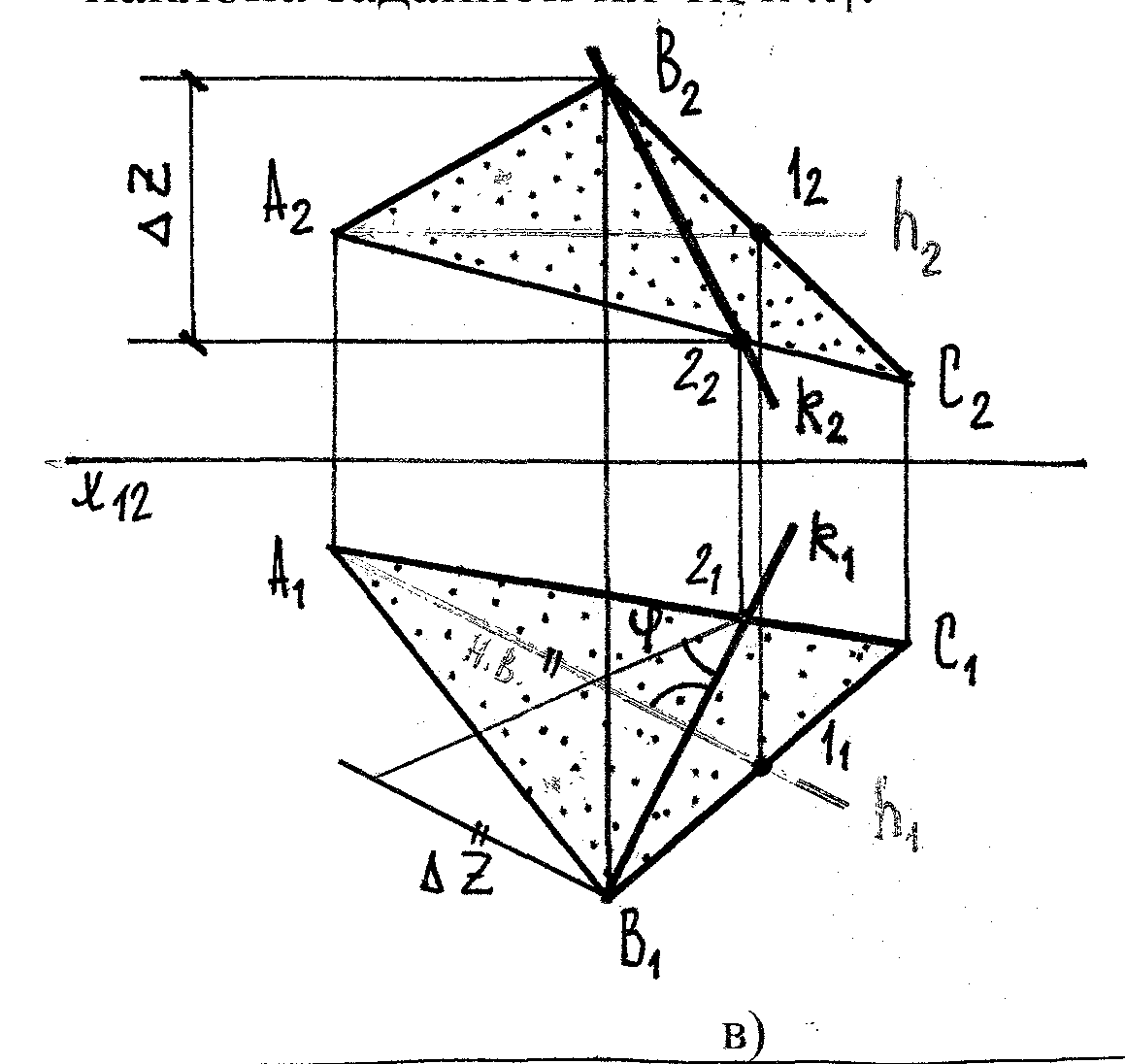k – линия ската;

k₁  h₁;

α – угол наклона

ΔАВС с π₁

Рис.23.

Лекция 4 Способы преобразования чертежа

Существует три типа задач:

1) конструктивные – задачи на построение геометрических фигур (их образов на чертеже), отвечающих заданным условиям.

2) позиционные – это задачи на взаимное расположение геометрических образов.

3)метрические – задачи на определение натуральных величин расстояний, углов и самих геометрических элементов.

Для облегчения решения задач, особенно метрических, возникает необходимость преобразования чертежей, т.е. их изменения. Это позволяет перевести геометрический элемент из общего положения в частное, при котором он будет проецироваться на плоскости пр-ий без искажения.

Существуют несколько видов преобразования чертежа. Мы рассмотрим два:

1. перемена плоскостей проекций;

2. вращение.