
- •Лекция №1
- •Литература:
- •Принятые обозначения и символика
- •1.1 Сущность операции проецирования
- •1.2 Методы проецирования
- •Ц ентральное проецирование
- •Параллельное проецирование
- •1.3 Общие свойства проецирования
- •1.4 Ортогональные проекции (прямоугольные проекции или метод Монжа)
- •1.5 Частные случаи расположения точек в пространстве
- •2.2 Изображение прямой общего положения на эпюре
- •2.3 Прямые частного положения
- •2.4 Принадлежность точки линии
- •2.5 Взаимное расположение прямых линий
- •2.6 Определение видимости геометрических элементов
- •Лекция 3
- •3.1 Плоскость
- •3.2 Плоскости общего положения
- •3.3 Плоскости частного положения
- •3.4 Признак принадлежности точки и прямой плоскости
- •3.5 Главные линии плоскости (особые)
- •Лекция 4 Способы преобразования чертежа
- •4.1 Перемена плоскостей проекций
- •4.1.1 Замена фронтальной плоскости проекций
- •4.1.2 Замена горизонтальной плоскости проекций.
- •Лекция 5
- •5.1 Способ вращения
- •Лекция 6
- •6.1 Поверхности
- •6.2 Линейчатые поверхности
- •6.3 Винтовые поверхности
- •6.4 Поверхности вращения
- •Лекция 7
- •7.1 Пересечение поверхностей
- •7.2 Свойство проецирующей поверхности:
- •7.2 Частный случай пересечения поверхностей
- •7.3 Общий случай пересечения поверхностей
- •7.4 Пересечение прямой с поверхностью или плоскостью (основная задача нг)
- •Лекция 8
- •8.1 Аксонометрические проекции
- •8.2 Прямоугольная изометрия
- •8.3 Прямоугольная диметрия
- •8.4 Построение плоских геометрических фигур в аксонометрии
- •8.5 Пересечение геометрических тел в аксонометрии
2.4 Принадлежность точки линии
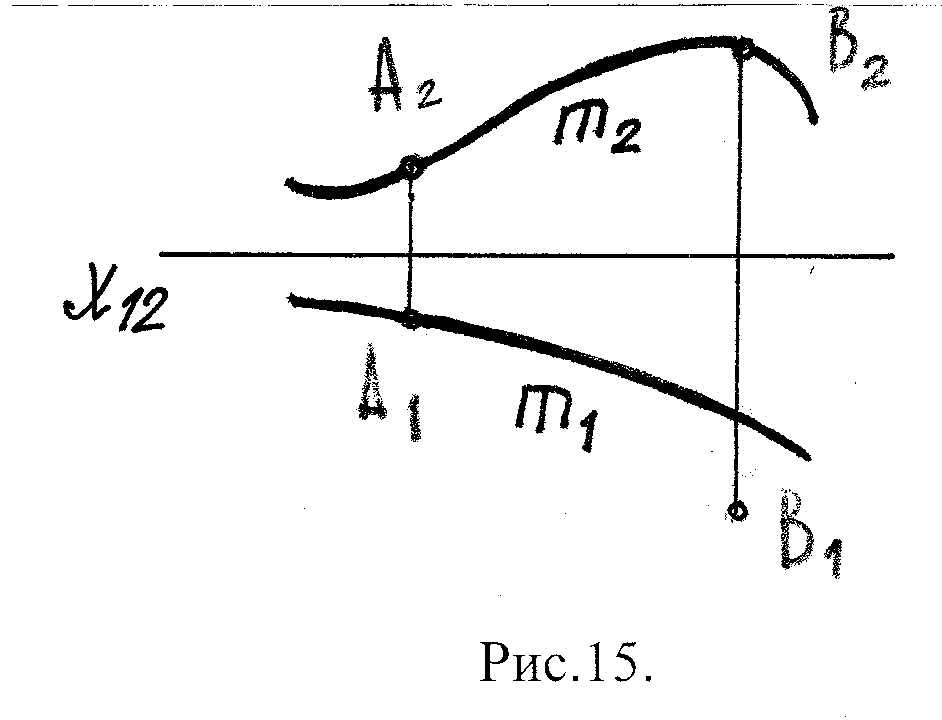 Зададим произвольную
линию, точки А и В.
Зададим произвольную
линию, точки А и В.
А m, т.к. А2 m2 и А1m1;
В m, т.к. В2 m2, а В1m1
Теорема : Точка принадлежит линии, если одноименные проекции точки лежат на одноименных проекциях линии.
2.5 Взаимное расположение прямых линий
Прямые в пространстве могут:
пересекаться;( перпендикулярными )
скрещиваться.( параллельными;)
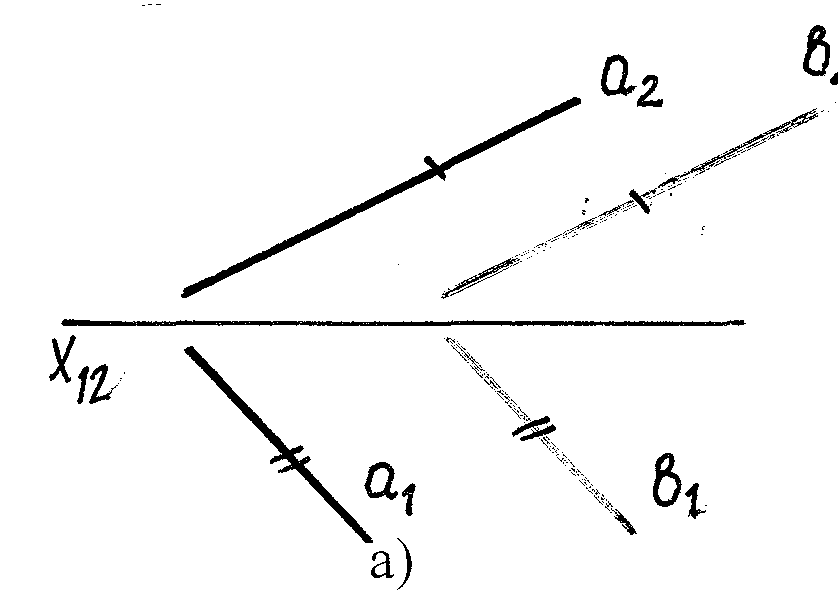
Две прямые a и b || в простр-ве, ес- ли они пересекаются в бесконечно
удаленной т-ке (в несобственной).
На черт. одноименные пр-ии прямых
параллельны (рис.16 а).
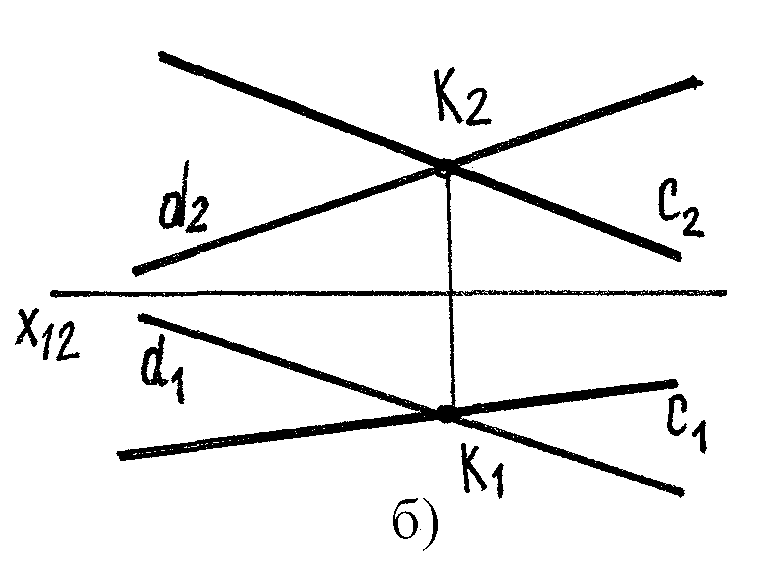
с и d пересекаются в простр-ве (с∩d)
с1∩d1 т.К1
с2 ∩d2 т.К2 на черт.
К1К2Х12
т.К – проекция точки пересечения с и d
(рис. 16 б)
Прямые пересекаются, если их одноименные проекции пере-секаются, а проекции точки пересечения лежат на одной линии связи (рис.16 в).
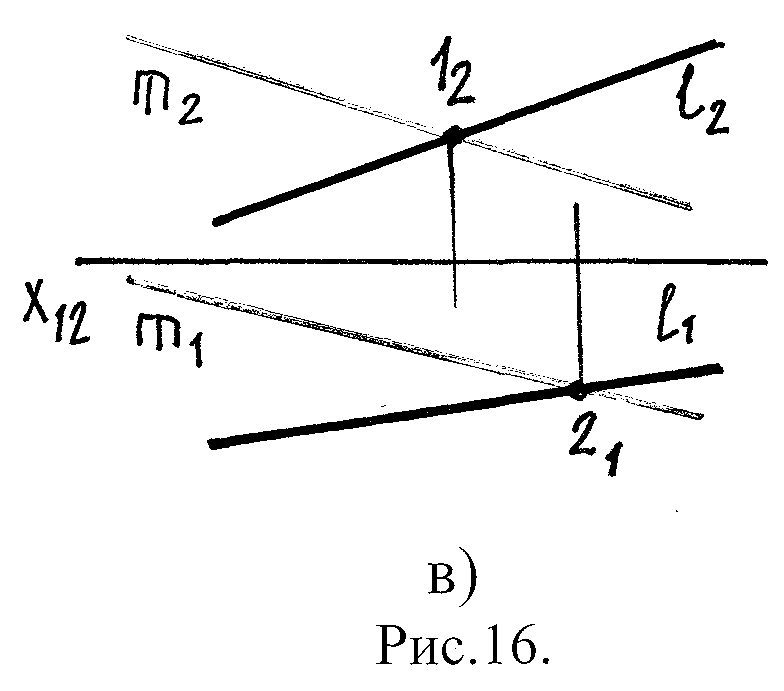
ℓ и m – скрещивающиеся прямые,
т.к. ℓ 2 ∩ m2 т.12 ≡ т.22 ,
т.1 т.2
Прямые скрещиваются, если они не пересекаются и не параллельны между собой, а точки пересечения их одноимённых проекций не лежат на одной линии связи.
2.6 Определение видимости геометрических элементов
Положение скрещивающихся прямых положено в основу метода конкурирующих точек, который используется для определения видимости поверхностей:
Видимость на горизонт. пр-ии определяется по фронтальной: видима та точка, которая расположена выше (больше высота).
В
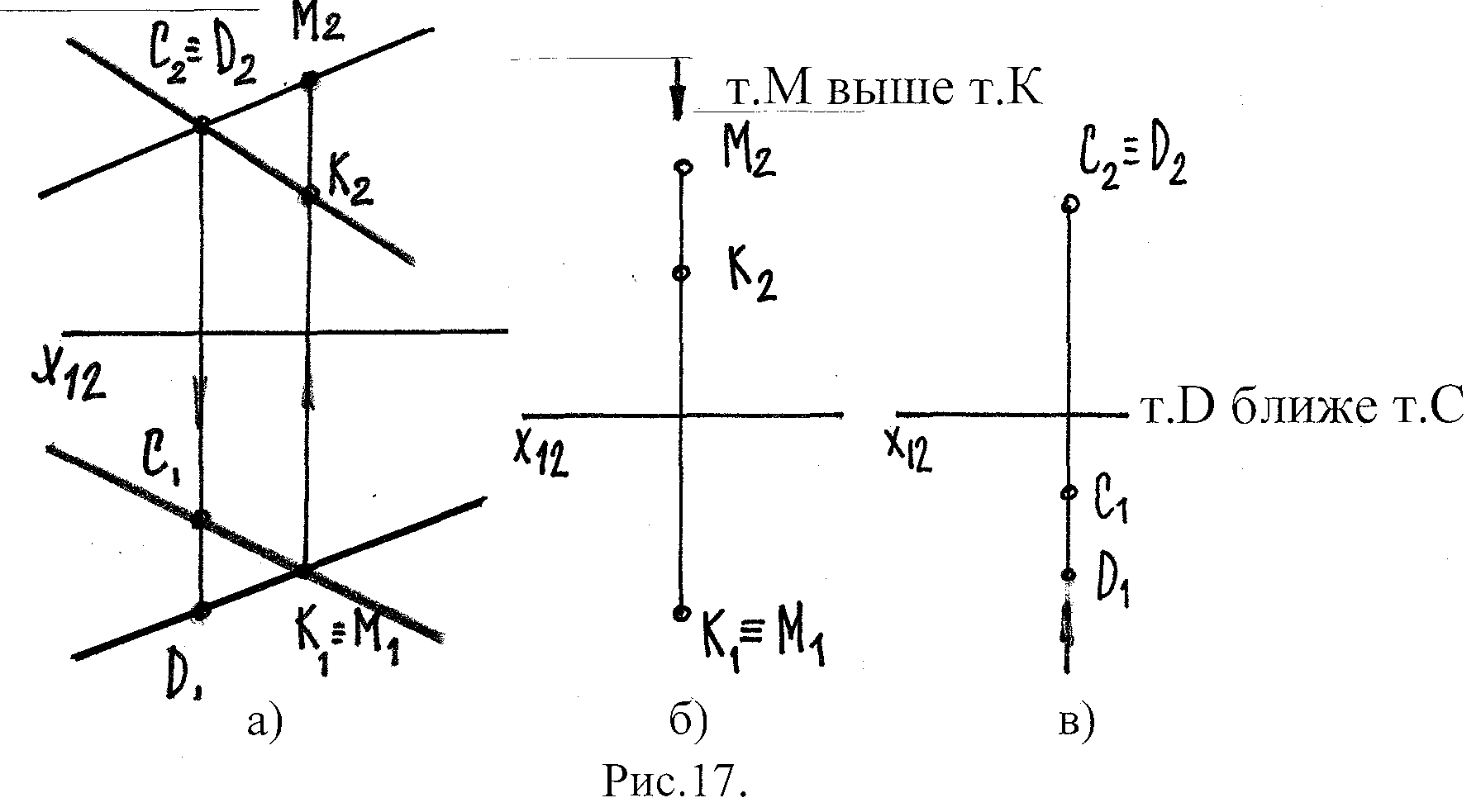 идимость
на фронт. пр-ии определяется по
горизонтальной: видима та точка, которая
расположена дальше от оси Х (больше
глубина).
идимость
на фронт. пр-ии определяется по
горизонтальной: видима та точка, которая
расположена дальше от оси Х (больше
глубина).
Лекция 3
3.1 Плоскость
Плоскость - частный случай поверхности на чертеже и задается определителем. Определитель – совокупность условий, состоящих из набора геометрических элементов, задающих тот или иной вид плоскости: ∑ (Г, А), где ∑ - обозначение пл-ти (поверхности);
Г, А - совокупность условий, задающих закон образования плоскости.
Пл-ти могут быть заданы следующими определителями (рис.18 а-д):
Тремя т-ми, не лежащими на одной прямой. (тремя несовпадающими т-ми).
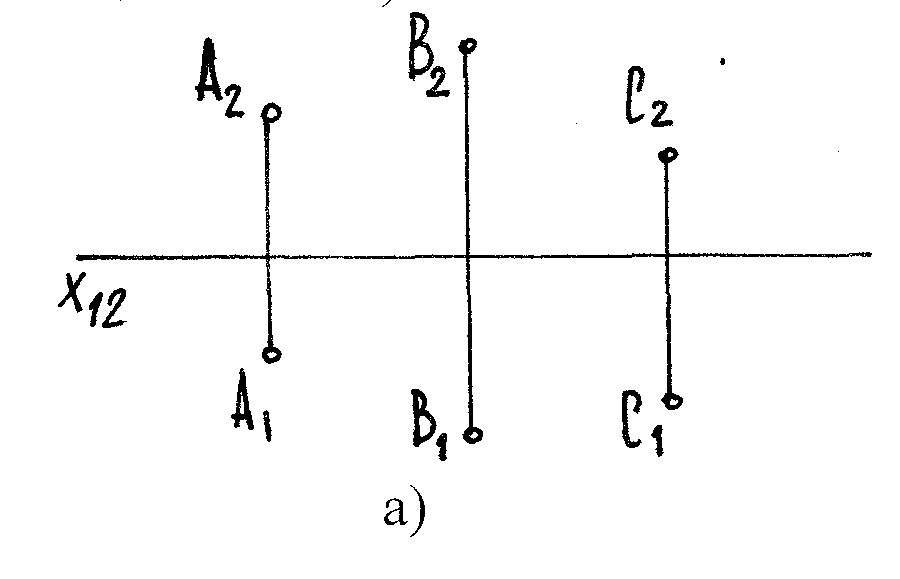
∑ (А,В,С)
Прямой и точкой, не лежащей на ней.
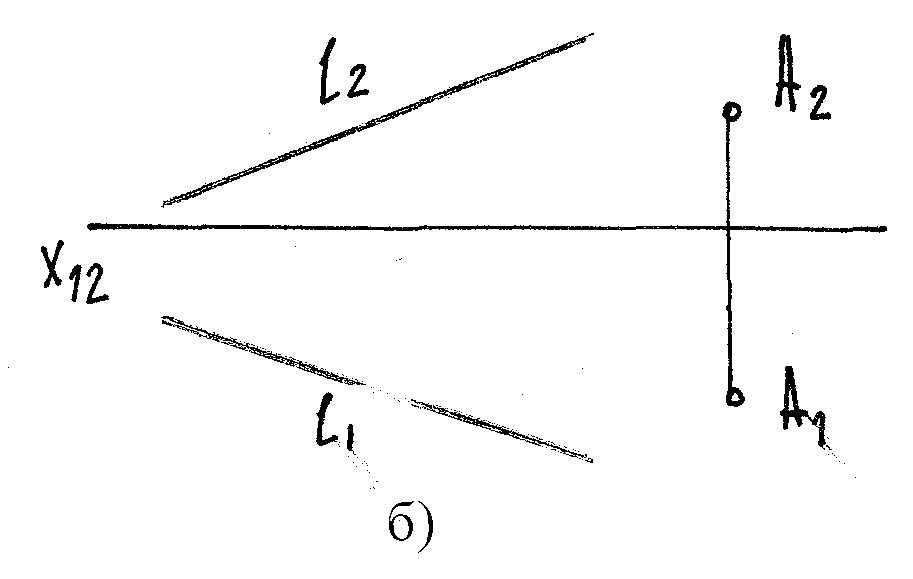 ∑ (ℓ,
А)
∑ (ℓ,
А)
Двумя пересекающимися прямыми.
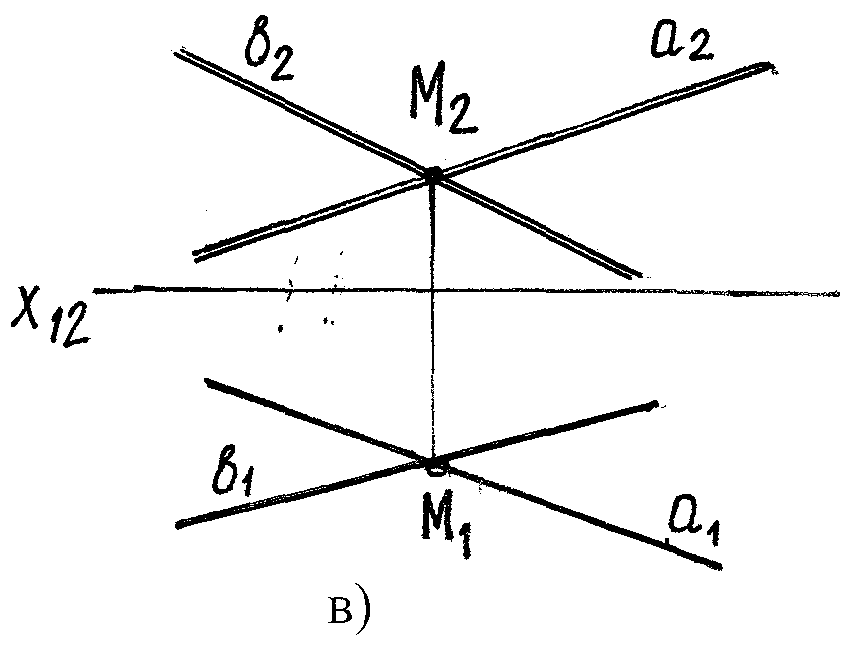 ∑ (a
∩ b)
∑ (a
∩ b)
Двумя параллельными прямыми.
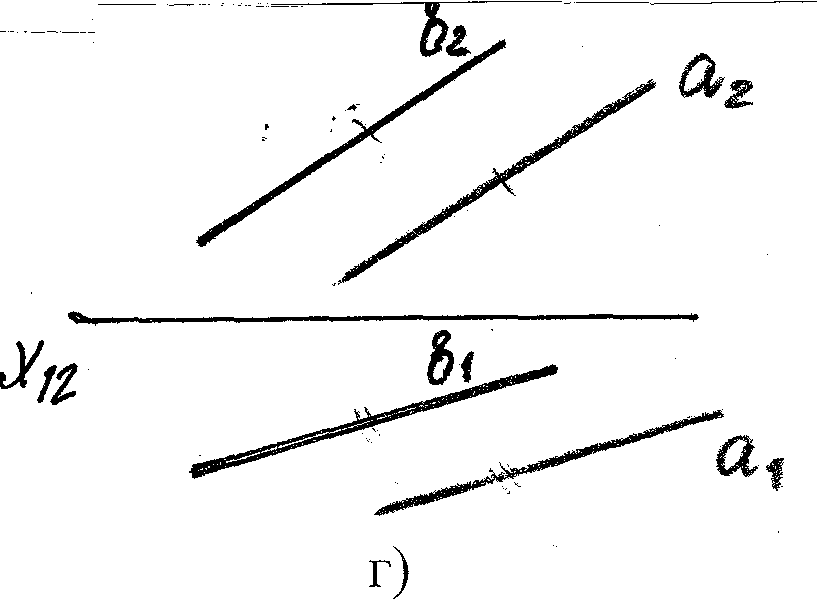 ∑ (a
|| b)
∑ (a
|| b)
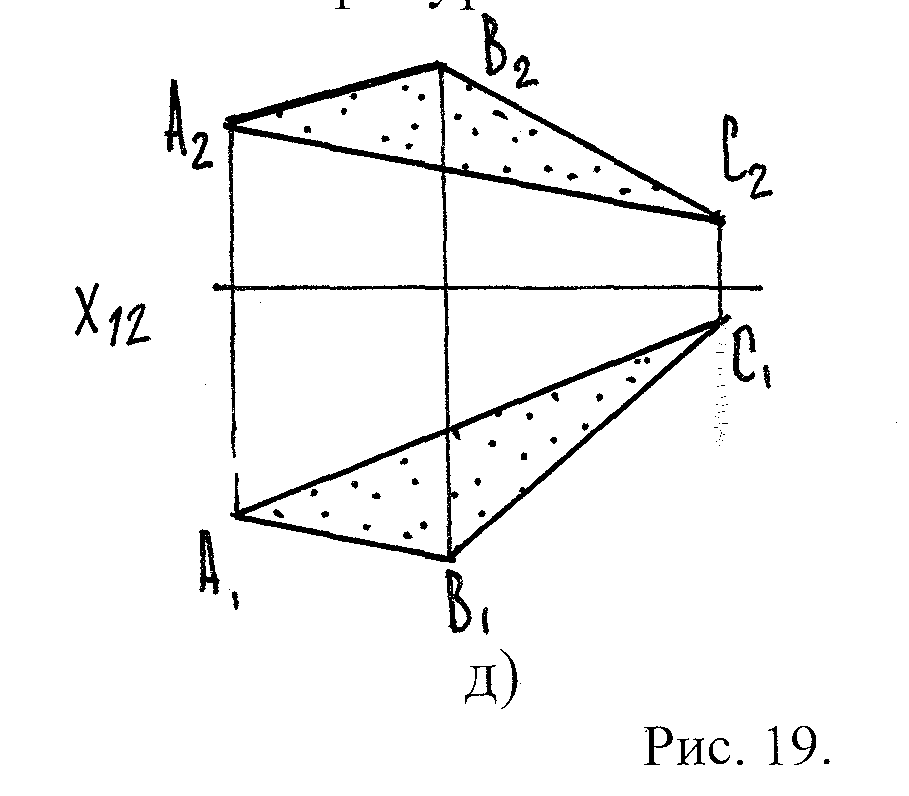
Плоской фигурой.
∑ ( АВС)
Также, как и прямые, пл-ти могут быть ||, какой-либо пл-ти проекций или быть пл-ми общего положения.
Итак, в зависимости от того, как расположена заданная пл-ть относительно плоскостей проекций, различают:
