1.5 Частные случаи расположения точек в пространстве

Любая точка, расположенная в пространстве, наз-ся т-кой оригинала. На эпюре она отсутствует, но, если точка  какой-либо плоскости проекций, то в этом случае, точка-оригинал совпадает с одной из своих проекций.

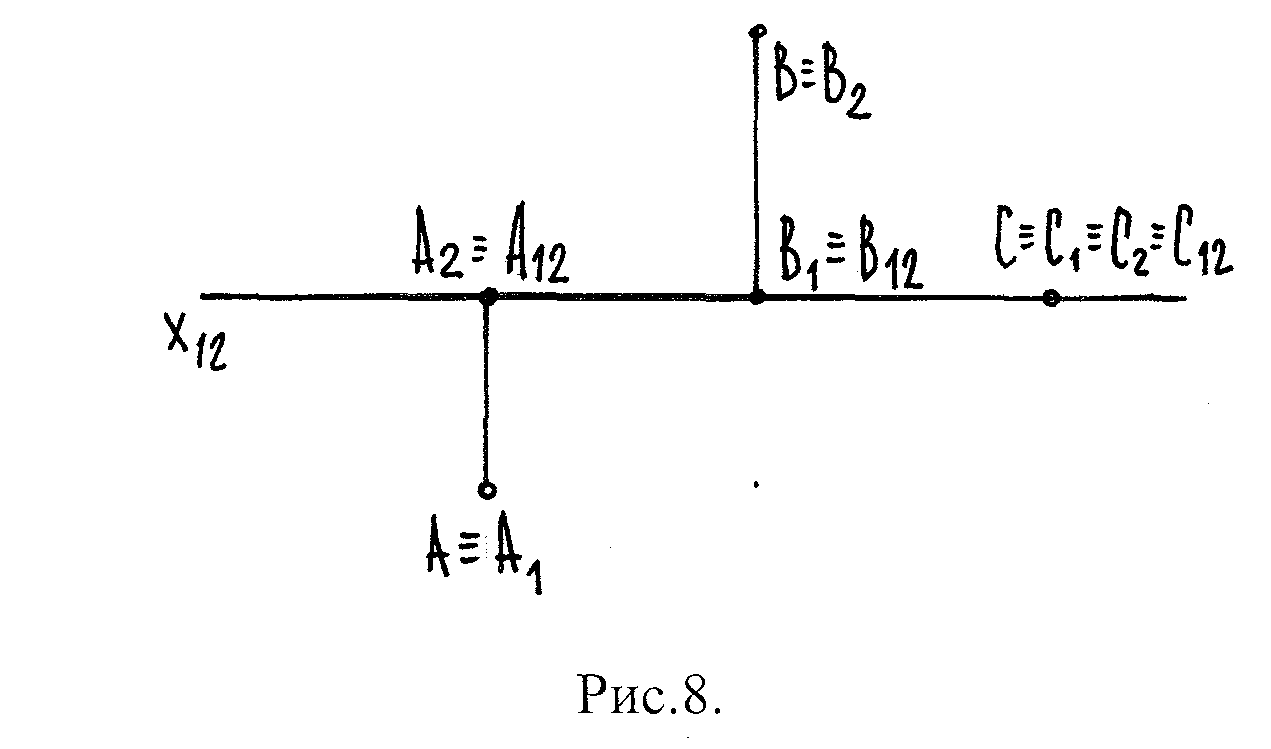
У т.А горизонт. пр-ия А₁ совпадает с т.А (А≡А₁). Фронт. пр-ия совпадает с осью Х₁₂ (А₂≡А₁₂). Точку В, расположенную на фронт. плоскости проекций: В≡В₂. Точка С одновременно  и плоскости π₁ и π₂.

1.6 Построение дополнительной профильной

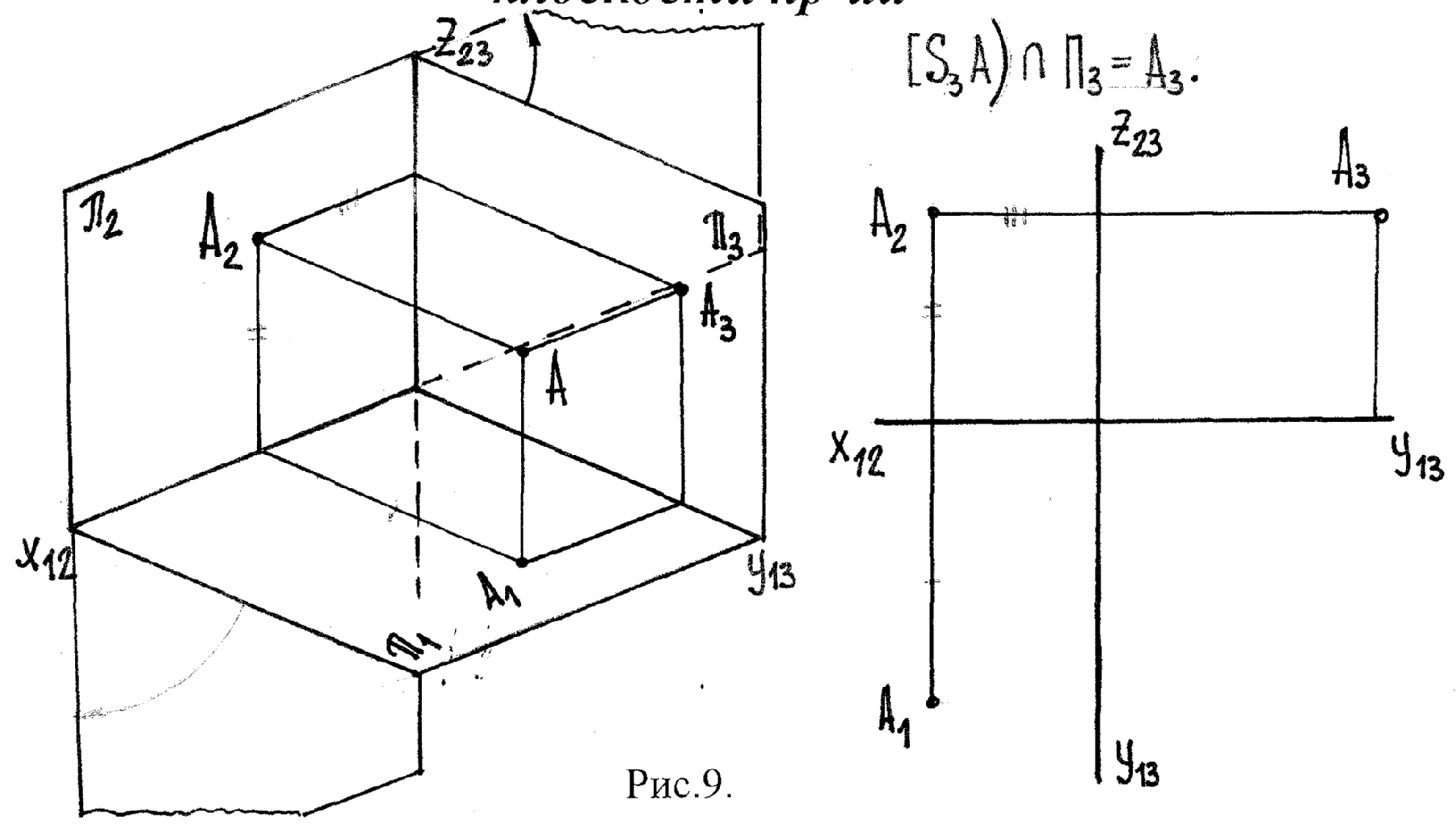плоскости проекций

π₃ – профильная плоскость проекций.

Пересечение π₁ и π₂ - ось Х₁₂,

Пересечение π₁ и π₃ - ось Y₁₃,

Пересечение π₂ и π₃ - ось Z₂₃.

А₃ – профильная проекция точки А.

Пл-ть π₁ развернём вниз, а пл-ть π₃ – назад. Ось Y раздваивается.

Развернув плоскости, получаем плоский чертёж. На этом основан координатный способ построения точки.

Лекция 2

2.1 Линии. Изображение линии на эпюре Монжа.

Простейшим геометрическим образом является линия. Приняты 2 способа образования линии:

1. Кинематический, т.е. линия рассматривается как траектория точки, непрерывно перемещающейся в пространстве.

2. Линия – это пересечение 2-х поверхностей.

На эпюре Монжа линия изображается двумя проекциями:

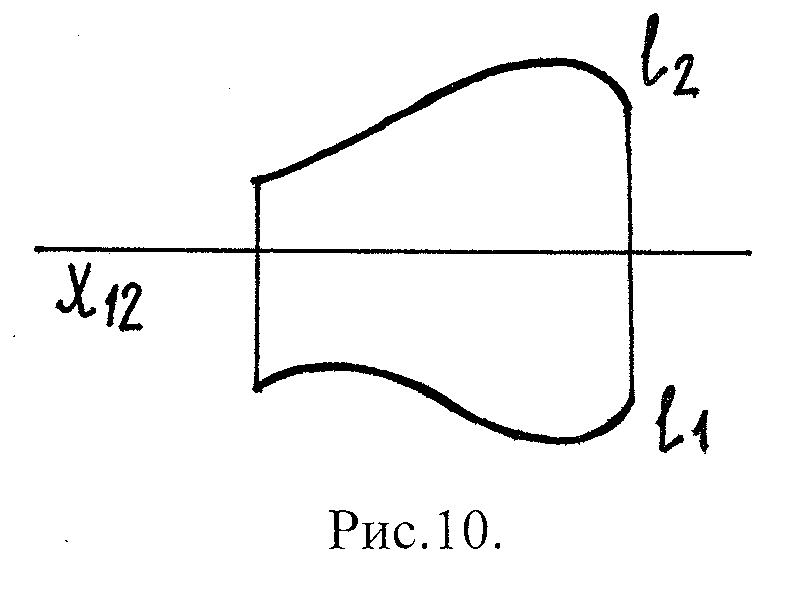
ℓ₁ - горизонтальная проекция;

ℓ₂ - фронтальная проекция

Линии бывают плоские и пространственные.

У плоских линий – все точки лежат в одной плоскости (окружность, эллипс, гипербола, парабола и т.п.).

Пространственные – это линии, все точки которых не лежат в одной плоскости (винтовая линия).

Для кривой линии вводится такая характеристика как порядок кривой, который определяется числом точек пересечения с прямой линией.

Например, кривая IV порядка.

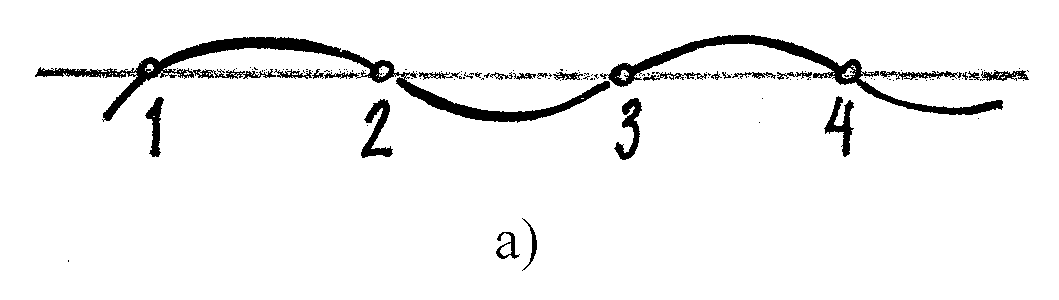
кривые II порядка: окружность, эллипс, гипербола.

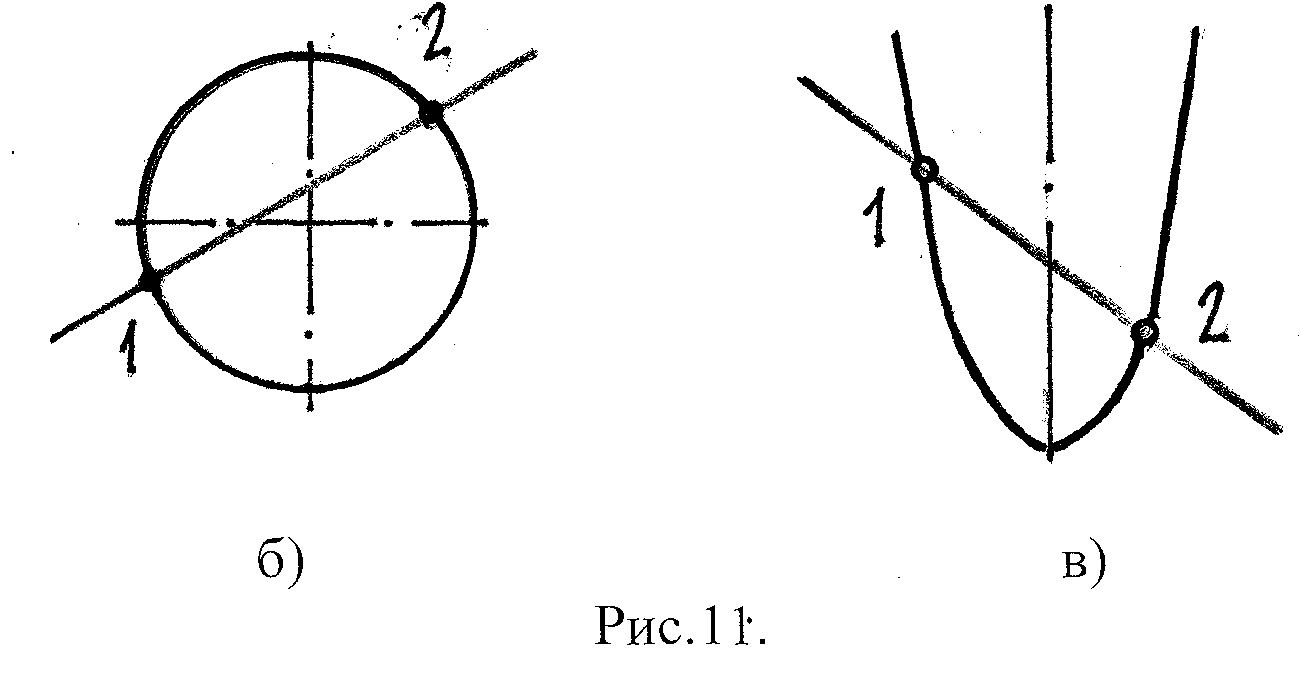
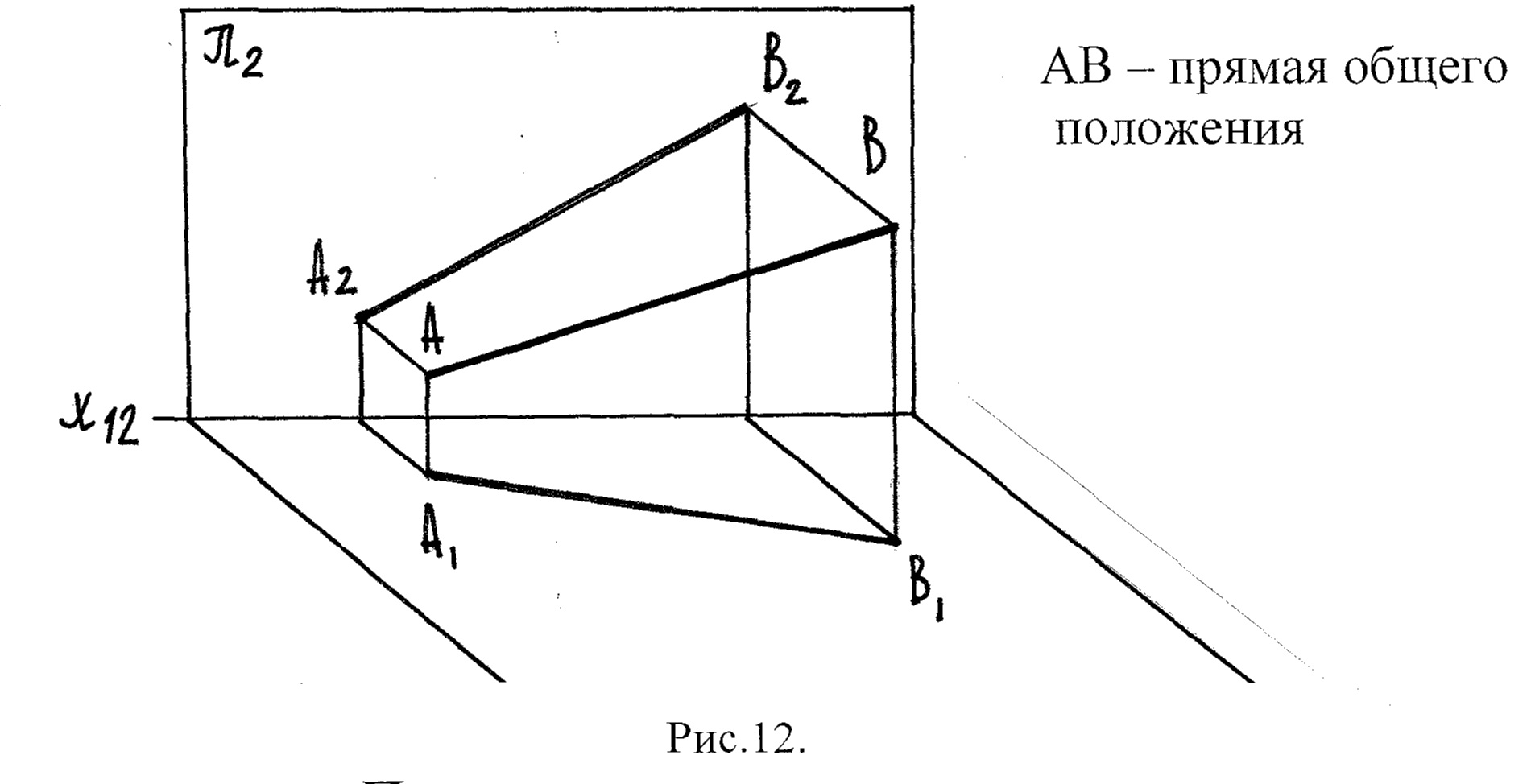
2.2 Изображение прямой общего положения на эпюре

Прямые в пространстве могут быть , || с плоскостями проекций, занимать общее положение.

Если прямая не || и не  ни одной из плоскостей проекций – она наз-ся прямой общего положения.

2.3 Прямые частного положения

Прямые частного положения – это прямые, параллельные или перпендикулярные какой-либо плоскости проекций. Существуют 6 прямых частного положения, которые, в свою очередь делятся на две группы:

2.3.1 Прямые уровня – это прямые, параллельные какой-либо плоскости пр-ий, их три (рис.13 а-в):

f – фронталь h – горизонталь p-профиль. прямая

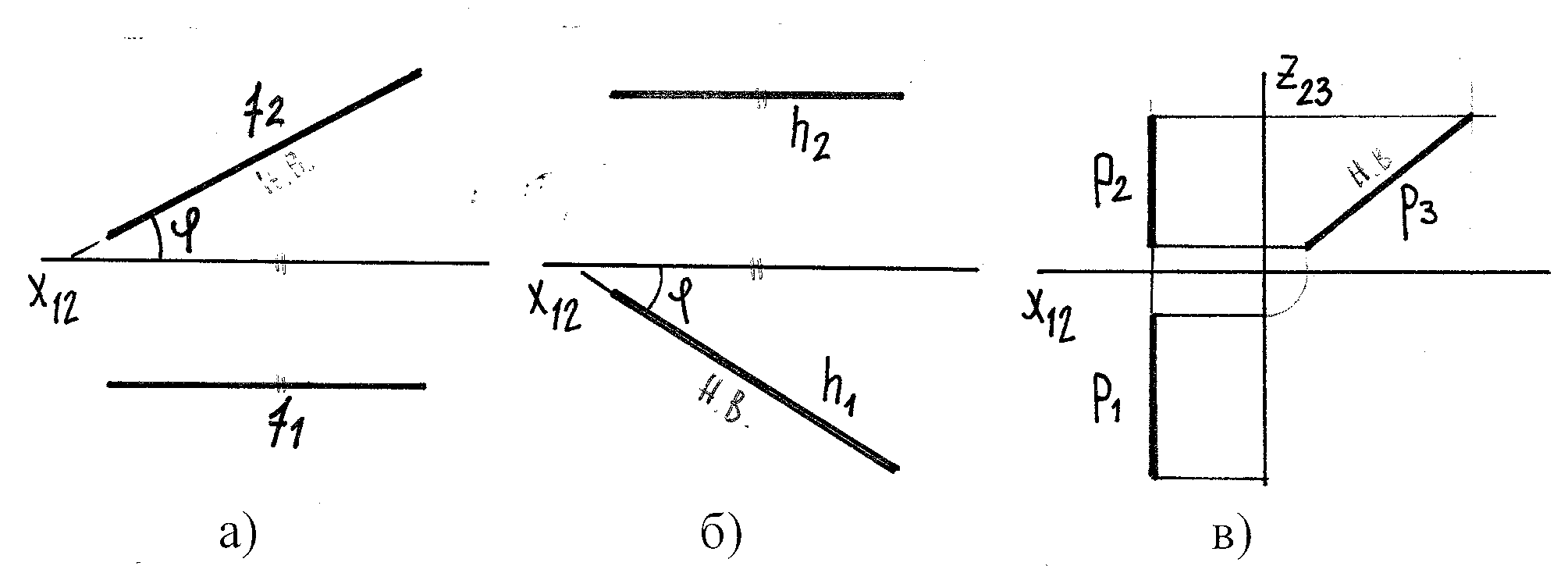
f || П₂ в простр-ве h || П₁ в простр-ве р || П₃ в простр-ве

f₂ – н.в. на черт. h₁ – н.в. на черт. р₃ – н.в. на черт.

f₁ || оси Х₁₂ h ₂ || оси Х₁₂ р₁ и р₂  Х₁₂

φ-угол с пл-тью π₁; φ- угол с пл-тью π₂;

2. Проецирующие прямые – это прямые, перпендикуляр-ные какой-либо плоскости проекций, их три (рис.13 г-е):

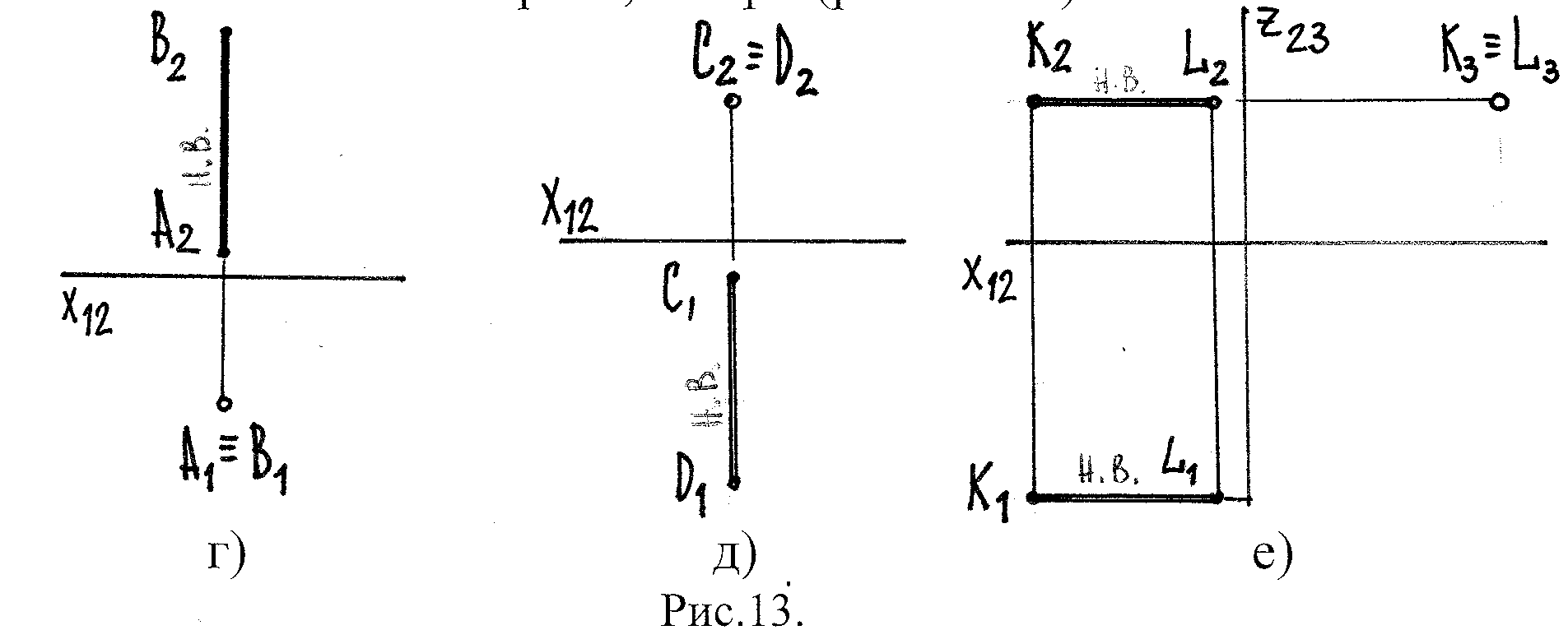
АВ-горизонт.-проецир. СД-фронт.-проецир. KL-профил.-проецир. прямая прямая прямая

АВ π₁ в простр-ве СДπ₂ в простр-ве КLπ₃ в простр-ве

А₂В₂Х₁₂ - н.в.на черт.С₁Д₁Х₁₂ – н.в. на черт. K₂L₂, K₁L₁ || Х₁₂ н.в.

А₁≡ В₁ – точка С₂ ≡ Д₂ – точка K₃ ≡ L₃ – точка

Если в пространстве прямая расположена в плоскости проекций, то на чертеже одна из ее проекций совпадает с осью Х₁₂

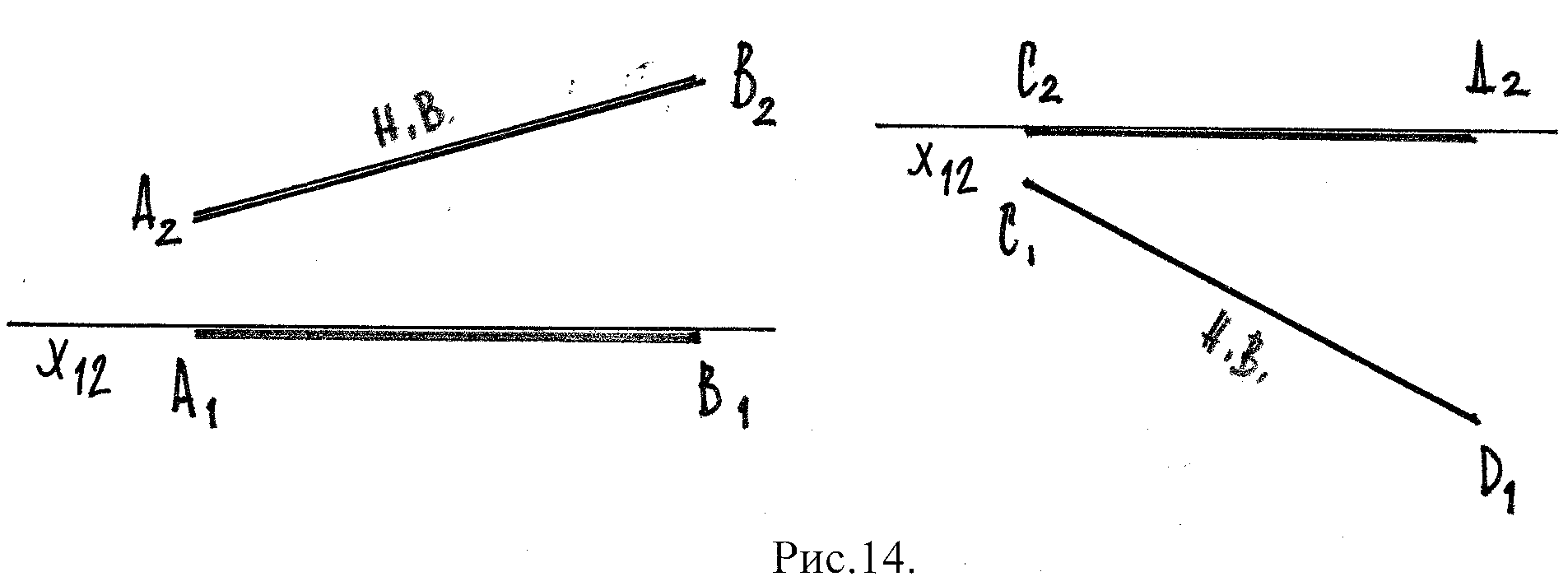
АВ  П₂ – в пространстве CD  П₁ – в пространстве

А₁В₁≡Х₁₂ на черт. С₂D₂ ≡ Х₁₂ на черт.

А₂В₂ – н.в. С₁Д₁ – н.в.