Направление 230200 – «Информационные системы»

Специальность 230201 – «Информационные системы и технологии»

Лекции по «Основам инженерной графики» без тем «Следы» и «Развертки поверхностей» (3-й семестр)

Лекция №1

Инженерная графика – дисциплина, изучающая вопросы изображения изделий на плоскости.

Литература:

1. Добряков. Курс начертательной геометрии

2. Добролюбов. Инженерная графика

3. Власов. Инженерная графика

Принятые обозначения и символика

1. Точки - прописными буквами латинского алфавита: А, В, С, D… или цифрами 1, 2, 3, 4…

2. Прямые и кривые линии – строчными буквами латинского алфавита: a, b, c, d….

3. Поверхности (пл-ть – это простейшая пов-ть) – прописными буквами греческого алфавита: Σ, Г, Φ…

4. Углы - строчными буквами греческого алфавита: α, β, …..

5. Линии уровня: горизонталь – h, фронталь – f

Основные операции:

∩ - пересечение или сечение;

U - объединение, союз;

≡ - тождество, совпадение;

• () - принадлежность;

 - перпендикулярность;

|| - параллельность;

- результат действия;

- - перекрещивание, скрещивание

Форму любого предмета можно рассматривать как сочетание отдельных простейших геометрических тел. А для изображения геометрических тел нужно уметь изображать их отдельные элементы: вершины (точки), ребра (прямые), грани (плоскости).

В основе построения изображений лежит метод проецирования. Получить изображение какого-либо предмета – значит спроецировать его на плоскость чертежа. Поскольку простейшим элементом любой фигуры является точка, изучение проецирования начинают с проецирования точки.

1.1 Сущность операции проецирования

Д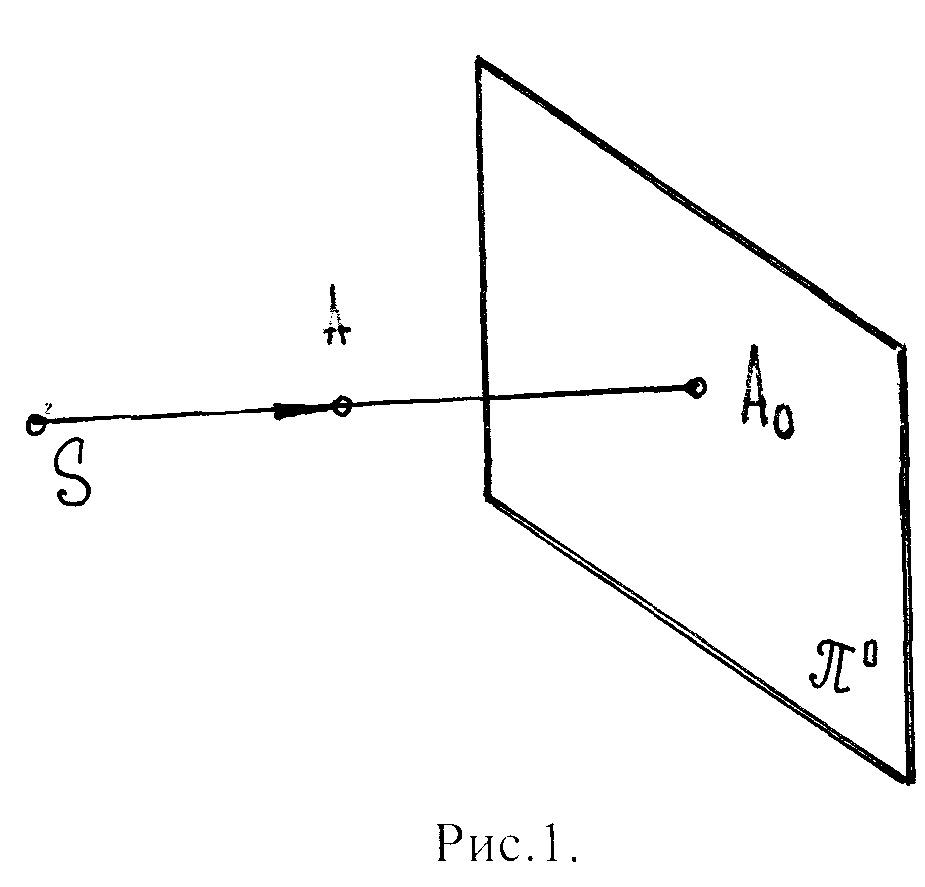 ля получения изображения точки А на плоскости π₀ (рис.1) через точку А проводят проецирующий луч SA. Точка пересечения этого луча с плоскостью π₀ будет ее проекцией на пл-ть π₀.

S – центр проецирования;

А₀ – проекция точки А на плоскость π₀

Итак, чтобы получить проекцию точки на пл-ть проекций, необходимо из центра проекций и точки в прострастве провести проецирующий невидимый луч до пересечения с пл-тью проекций. Полученная точка наз-ся проекцией точки или изображением точки.

Обозначим все эти действия с помощью условных обозначений.

Дано: π₀ и S, т.А

Решение: 1) S∩т.А  SА - принцип проецирования

2) SА∩π₀А₀

1.2 Методы проецирования

В зависимости от положения точки S относительно пл-ти проекций, проецирование делится на 2 вида:

1. Ц ентральное проецирование

S- конечная точка (собственная).

А, В, С – произвольные точки, -щие линии ℓ.

Через каждую из них проводятся линии (лучи) до пересечения с π₁. Все проецирующие лучи исходят из одного центра.

Соединив проекции т-ек А₁, В₁, С₁, получим проекцию линии ℓ₁.

Лучи создают коническую поверхность Σ, она пересекается с пл-тью π₁.

Σ ∩ π₁

Σ  ℓ;  ℓ₁(А₁, В₁, С₁) – центральная проекция линии ℓ.

2. Параллельное проецирование

S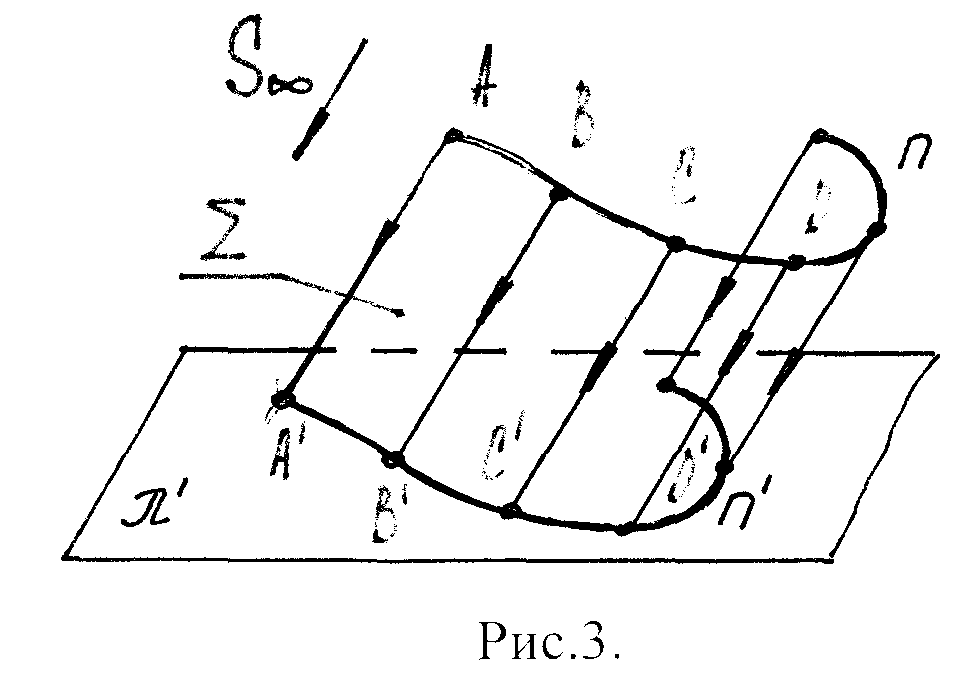 ^∞ - бесконечно удаленная точка. Через каждую т-ку линии n проводятся лучи, параллельно заданному направлению.

Создали цилиндрическую поверхность Σ и решили ту же задачу, что и выше.

В свою очередь, параллельное проецирование делится на 2 вида, в зависимости от угла наклона проецирующих лучей к пл-ти проекций:

а) прямоугольное или ортогональное проецирование

К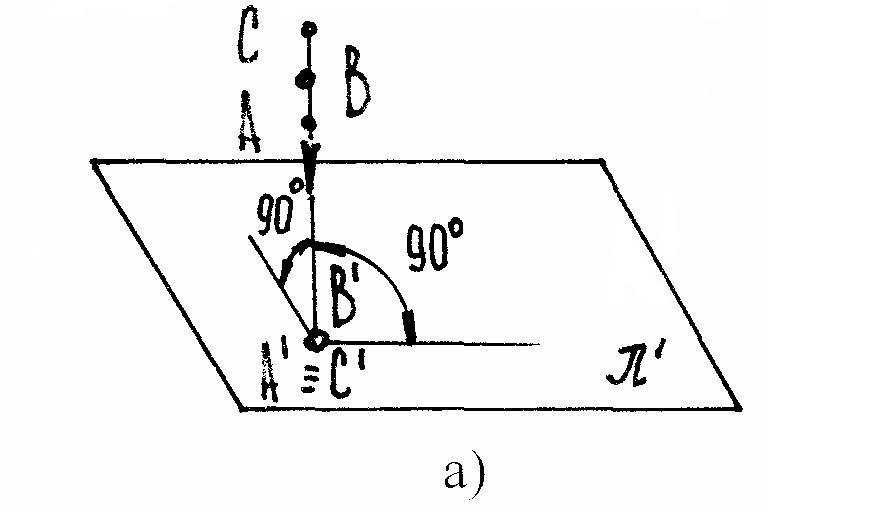 аждый луч проходит отно- сительно пл-ти под углом 90⁰.

Какое бы кол-во т-ек на луче не брать, их проекциями на π' явля-ется В' (рис.4а) А'≡ В'≡ С'. Черт. необратим, т.к. т-ке В' соответст-вует каждая из т-ек, принадлежащих этому лучу.

б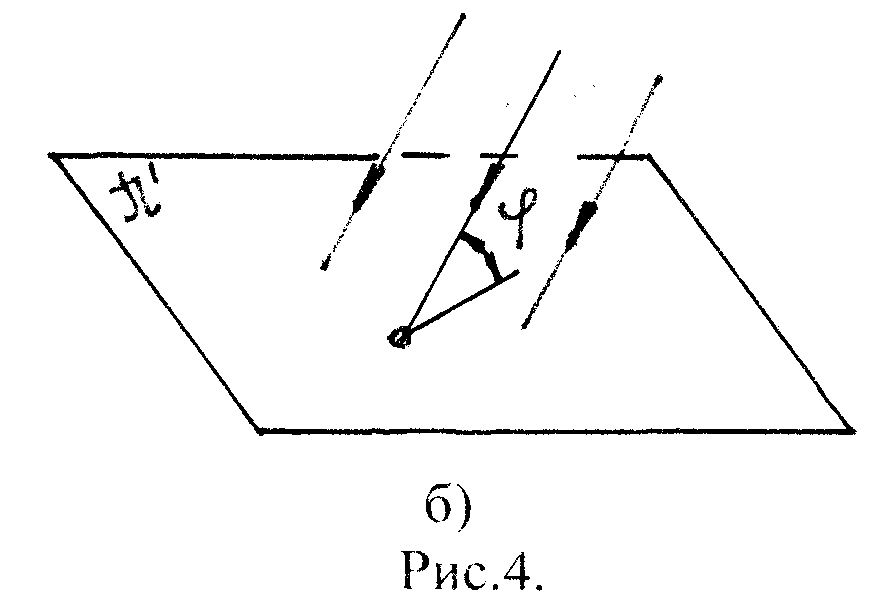 ) косоугольное проецирование

φ - угол наклона проецирующего

луча к пл-ти проекций