
Министерство образования и науки Российской Федерации Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В ИЗУЧЕНИИ СВОЙСТВ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Методические указания к выполнению лабораторной работы по дисциплине «Измерительный практикум»
для студентов направления подготовки
03.03.02«Физика» (уровень бакалавриата) очной формы обучения
Красноярск 2015
УДК 53.08(076)
Рецензент кандидат физико-математических наук, доцент О. П. ЗОЛОТОВА
(Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева)
Печатается по решению методической комиссии НОЦ ИКИВТ
Метод наименьших квадратов в изучении свойств мате-
матического маятника : метод. указания к выполнению лаб. работы по дисциплине «Измерительный практикум» для студентов направления подготовки 03.03.02 «Физика» (уровень бакалавриата) очной формы обучения / сост.: О. П. Вайтузин, Е. П. Пьяновская, А. С. Паршин ; Сиб. гос. аэрокосмич. ун-т. – Красноярск, 2015. – 18 с.
© Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева, 2015
2
ОБЩИЕ СВЕДЕНИЯ
Любой научный эксперимент, как правило, сводится к серии измерений той или иной величины, зависящей от изменения других параметров. Поэтому неизбежным этапом работы физика-исследователя является изучение экспериментальной зависимости между этими физическими характеристиками. Однако построить функциональную зависимость, наилучшим образом описывающую изменение интересующей нас физической величины, невозможно. Это связано с тем, что любые данные, полученные экспериментально, имеют погрешности.
Существующие математические методы позволяют нам построить некую функциональную зависимость таким образом, чтобы отклонения кривой от полученных экспериментальных данных были минимальными.
Приближенное выражение сложной функции, полученной экспериментально, с помощью другой более простой непрерывной функции называется аппроксимацией (от лат. approximare − приближаться).
Чем больше количество экспериментальных данных, тем меньше погрешность. Для каждой конкретной аппроксимируемой функции нужно стремиться выбрать такой способ аппроксимации, который обеспечивает минимальную погрешность.
Вданной лабораторной работе речь пойдет об одном из методов аппроксимации, который достаточно часто применяется при математической обработке экспериментальных данных – методе наименьших квадратов (МНК).
Вметоде наименьших квадратов аппроксимирующая функция может не совпадать ни с одним значением, полученным с помощью эксперимента, но максимально приближаясь к ним в среднем.
Данные методические указания содержат краткие теоретические сведения о методе наименьших квадратов и колебательных процессах, описание экспериментальной установки, порядок выполнения лабораторной работы, контрольные вопросы и библиографический список с рекомендуемой литературой.
Методические указания предназначены для студентов направления подготовки 03.03.02 «Физика» (уровень бакалавриата) очной формы обучения при изучении ими дисциплины «Измерительный практикум» и могут быть использованы при выполнении других лабораторных работ по дисциплинам «Общий физический практикум» или «Специальный физический практикум» и других дисциплин.
3

Лабораторная работа
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В ИЗУЧЕНИИ СВОЙСТВ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Цель работы: получение навыков обработки экспериментальных данных методом наименьших квадратов и оценка погрешности реализации этого метода на примере изучения гармонических колебаний математического маятника.
Оборудование: модульный учебный комплекс МУК-М1.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Метод наименьших квадратов
Метод наименьших квадратов – метод оценки экспериментальных измерений с помощью аппроксимации такой функцией, которая справедлива во всем диапазоне данных, но не точно совпадает с ними, а максимально приближена к ним. Этот метод был предложен в XVIII в. немецким математиком К. Гауссом.
Суть метода наименьших квадратов состоит в минимизации суммы квадратов отклонений (дисперсии) между значениями аппроксимирующей функции и экспериментальными данными.
Выбор именно суммы квадратов отклонений, а не алгебраической суммы отклонений объясняется очень просто: во-первых, квадрат любого числа всегда неотрицателен и сумма квадратов всегда неотрицательна, т. е. ограничена снизу, а следовательно у нее есть минимум; во-вторых, при нахождении минимальной суммы квадратов мы уменьшаем максимальную ошибку.
Чаще всего данные, полученные экспериментально, связаны между собой линейной зависимостью, которая представляет собой прямую на плоскости (в пространстве двух измерений) и задается уравнением
y = ax + b, |
(1) |
где у – значение функции; х – аргумент; а, b – параметры функций, которые необходимо подобрать так, чтобы сама функция располагалась как можно ближе к экспериментальным точкам (a – угловой коэффициент, b – свободный член).
4
Для нахождения коэффициентов а, b искомой прямой необходимо минимизировать сумму квадратов расстояний yi по ординате
от |
точки |
(хi; |
yi) до прямой. Расстояния yi определяются как |
yi |
= yi − |
axi − |
b. Как известно, необходимым условием того, что |
функция приобретает минимальное значение, является то, что ее первая производная (или частные производные для функции многих переменных) равна нулю.
n
Для минимизации ∑ yi2 , где n – количество эксперименталь-
i=1
ных данных, приравняем к нулю производные этой суммы по параметрам а, b:
|
|
∂ |
n |
|
n |
|
|
|
|
|
|
= ∑( yi − axi |
− b)2 |
= 2∑( yi − axi − b)(−xi ) = 0, |
|
|
∂a |
|
|||||
|
i=1 |
|
i=1 |
(2) |
|||
|
|
∂ |
n |
|
n |
||
|
|
|
|||||
|
|
|
|
= ∑( yi − axi |
− b)2 |
= 2∑( yi − axi − b)(−1) = 0. |
|
|
|
∂b |
|
||||
|
|
i=1 |
|
i=1 |
|
||
Преобразуем эту систему: |
|
|
|
||||
|
|
|
|
n |
n |
n |
|
|
|
|
|
а∑ xi2 + b∑ xi − ∑ xi yi = 0, |
|
||
|
|
|
|
i=1 |
i=1 |
i=1 |
(3) |
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
а∑ xi + bn − ∑ yi = 0. |
|
||
|
|
|
|
i=1 |
i=1 |
|
|
Решая полученную систему нормальных уравнений относительно а, b, имеем
|
n |
|
n |
n |
|
|
|
n |
n |
|
|
|
n∑ xi yi −∑ xi ∑ yi |
|
|
∑ yi − a∑ xi |
|
||||||
а = |
i=1 |
i=1 |
i=1 |
, |
b = |
i=1 |
i=1 |
. |
(4) |
||
|
|
|
|
2 |
|
|
|||||
|
n |
n |
|
|
|
|
n |
|
|||
|
n∑ xi2 − |
∑ xi |
|
|
|
|
|
|
|
||
|
i=1 |
i=1 |
|
|
|
|
|
|
|
|
|
где xi, yi – экспериментальные данные.
Вычисляя из n опытов необходимые суммы и производя указанные выше действия, получаем величину коэффициентов а, b. Подставив найденные коэффициенты a и b в уравнение (1), получим вид теоретической прямой, которая описывает изменение экспериментальных данных (рис. 1).
На рис. 1 светлыми точками обозначены экспериментальные данные. Аппроксимирующая функция, построенная с помощью двух
5
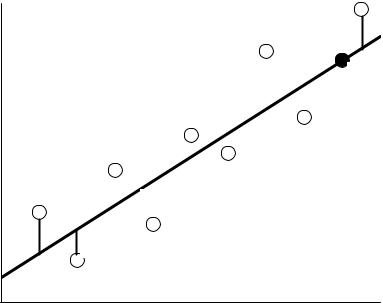
точек M и N, показана прямой линией. Расстояния по ординате от экспериментальных данных до аппроксимирующей прямой обозначены yi.
уy
уynn
N
 MМ
MМ
уy11 yу22
x
х
Рис. 1. Графическая иллюстрация метода наименьших квадратов (обозначения см. в тексте)
На практике линейная зависимость между двумя величинами встречается не всегда. В таком случае следует провести линеаризацию зависимости путем такой замены переменных, чтобы преобразованная зависимость соответствовала уравнению (1).
Оценка погрешности метода наименьших квадратов
Как мы уже выяснили, задачей метода наименьших квадратов для линейной аппроксимирующей функции является вычисление параметров функции: углового коэффициента a и свободного члена b. Однако следует понимать, что для каждой конкретной серии измерений величины a и b будут случайными и повторение серии измерений даст нам уже другие, несколько отличающиеся значения a и b.
Следовательно, кроме вычисления параметров линейной аппроксимирующей функции, требуется найти доверительные интервалы для искомых параметров a и b, в которых данные значения существуют, т. е. определить их отклонения от истинных значений.
6

Математическая статистика дает следующее выражение для среднеквадратичного отклонения Sa случайной величины a от истинного углового коэффициента:
|
|
|
Sа = |
|
Q |
, |
(5) |
|
|
|
|
|
n |
||||
|
|
|
|
(n − 2)∑(xi − xср )2 |
|
|
||
|
|
|
|
|
i=1 |
|
|
|
|
|
1 |
n |
|
|
|
||
где xср |
= |
∑ xi – среднее арифметическое значение x, |
а Q – сумма |
|||||
|
||||||||
|
|
n i=1 |
|
|
|
|||
квадратов отклонений: |
|
|
|
|||||
|
|
|
|
n |
|
|
|
|
|
|
|
Q = ∑(axi |
+ b − yi )2 ; |
|
(6) |
||
i =1
здесь a и b вычислены по формуле (4).
Среднеквадратичное отклонение случайной величины b от истинного свободного члена может быть представлено в следующем виде:
S |
|
= |
Q |
+ x2 |
S 2 . |
(7) |
|
b |
n(n − 2) |
||||||
|
|
ср |
a |
|
|||
|
|
|
|
|
|
Погрешность параметров a и b принимается равной полуширине доверительного интервала и находится как произведение соответствующего среднеквадратичного отклонения на коэффициент Стьюдента для доверительной вероятности 68 % и числа измерений n. Следует учитывать, что в данном случае для коэффициента Стьюдента число степеней свободы меньше числа измерений на 2 и равно (n – 2).
Можно дополнительно вычислить относительные погрешности a и b, разделив соответствующие абсолютные погрешности на числовые значения a и b.
Колебания
Колебания – движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания представляют собой один из наиболее распространенных видов движения в природе и технике.
7
Колебания могут быть разной природы: механическими, электромагнитными, электромеханическими и др. В зависимости от характера воздействия на колеблющуюся систему различают свободные (собственные), затухающие, вынужденные колебания, а также автоколебания и параметрические колебания.
Свободными, или собственными, называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как она была выведена из положения равновесия.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы.
Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешней силы, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой, т. е. система сама управляет внешним воздействием.
При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы.
Простейшим видом колебаний являются гармонические колебания. Это такие колебания, при которых колеблющаяся величина изменяется по закону синуса (или косинуса). Этот вид колебаний особенно важен, так как многие колебания часто имеют характер, очень близкий к гармоническим колебаниям. Периодические процессы иной формы, т. е. с другой зависимостью от времени, могут быть представлены как наложение нескольких гармонических колебаний.
Колебательные процессы характеризуются следующими физическими величинами:
–периодом колебаний Т – временем, за которое совершается одно полное колебание: T = t/N, где N – количество колебаний. Выражается в секундах (с);
–частотой колебаний ν – числом колебаний в 1 с. Это величи-
на, обратная периоду: ν = 1/Т = N/t. Измеряется в герцах (Гц), имеет размерность [с–1 ];
–круговой (угловой, циклической) частотой ω – числом полных колебаний, которые совершаются за 2π единиц времени (секунд):
ω= 2πν = 2π/T. Тогда T = 2π/ω. Единица измерения – радиан в секунду (рад/с);
–фазой колебаний ϕ – физической величиной, показывающей, какая часть колебания прошла с начала процесса, и определяющей смещение x в данный момент времени. Измеряется в угловых величи-
8
нах – градусах или радианах. Фаза колебания в начальный момент времени (t = 0) называется начальной фазой ϕ0: ϕ = ϕ0 + ωt;
–смещением (х) – отклонением колеблющейся точки от положения равновесия в данный момент времени;
–амплитудой колебаний А – наибольшим смещением от положения равновесия. Амплитуда А – постоянная положительная величина: A = |xmax|. Если колебания незатухающие, то амплитуда постоянна.
Уравнение гармонических колебаний можно представить в виде
|
|
x(t) = Аcos(ωt + ϕ0 ), |
x(t) = Аsin(ωt + ϕ0 ), |
(8) |
|
где A – амплитуда; ω – круговая частота; t – |
аргумент функции, теку- |
||||
щее |
время; |
ϕ0 – начальная фаза; |
ωt + ϕ0 – |
фаза колебания |
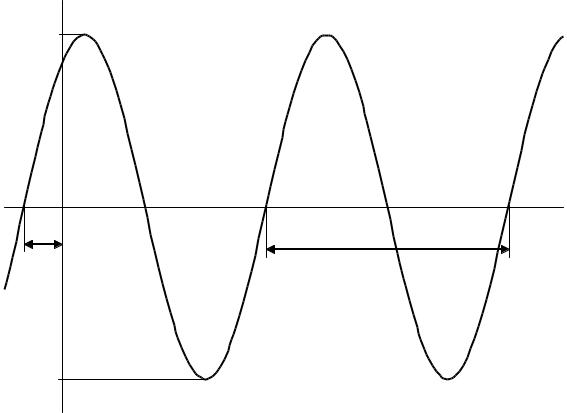
(рис. 2). |
В случае строго гармонического, |
незатухающего колебания |
величи- |
|||
ны А, ω и ϕ0 не зависят от времени. |
|
|
|||
|
хx |
|
|
|
|
|
A |
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
tt |
|
ϕ0 |
|
ТT==2ππ/ω/ ω |
|
|
|
ω |
|
|
|
|
|
– А-A |
|
|
|
|
|
|
Рис. 2. График зависимости x(t) = Asin(ωt + ϕ0) |
|
||
Косинус может изменяться в пределах от –1 до +1, поэтому значения x(t) лежат в пределах от – А до +А.
Начальная фаза ϕ0 зависит от положения начала отсчета времени. Следовательно, значение ϕ0 определяется выбором начала отсчета
9

времени. Так как значение x(t) не меняется при добавлении или вычитании из фазы целого числа 2π, то всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматривают только значения ϕ0, лежащие в пределах от – π до +π.
Наиболее наглядно колебательный процесс демонстрирует качающийся маятник.
Колебания математического маятника
Математическим маятником называют идеализированную систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик массой m, подвешенный на тонкой длинной нити, при условии, что радиус шарика много меньше длины нити l. Если маятник отклонить от положения равновесия на небольшой угол x, где x – угол, образованный нитью с вертикалью, и отпустить его, то маятник начнет совершать колебательное движение. Траекторией движения шарика будет дуга окружности радиусом l. На шарик при движении будут действовать две силы: сила тяжести mg, направленная вертикально вниз, и сила упругости нити F, направленная вдоль нити (рис. 3). Конечно, при движении маятника на него будет действовать и сила сопротивления воздуха, но мы будем считать ее пренебрежимо малой.
Рассмотрим маятник в произвольный момент времени t в процессе колебаний. Пусть x – угол отклонения от вертикали в этот момент.
Запишем уравнение второго закона Ньютона в проекции на касательную ось z, показанную на рис. 2:
mat = −mg sin x , |
(9) |
где g – ускорение свободного падения.
Принимая во внимание связь линейного ускорения at и углового
&& |
, имеем |
|
|
ускорения ε = x |
|
|
|
|
at |
= εl = xl , |
(10) |
|
|
&& |
|
2
где l – длина нити; &&x = d x – вторая производная x по времени t. dt2
10
