Тема 6.3 Елементи теорії різницевих рівнянь

1. Що таке сітки та сіткові функції.

2. Лінійні звичайні різницеві рівняння.

3. Лінійні однорідні різницеві рівняння.

4. Неоднорідні різницеві рівняння.

5. Застосування різницевих рівнянь в економіці.

Розділ 7. Ряди Тема 7.1. Числові ряди

1. Що називається числовим рядом? Що називається загальним членом ряду? Навести приклади.

2. Який ряд називається збіжним? Що називається його сумою? Який ряд називається розбіжним? Навести приклади.

3. Сформулювати і довести необхідну ознаку збіжності ряду. У чому полягає найпростіша достатня ознака розбіжності ряду? Навести приклади.

4. Сформулювати і довести такі достатні ознаки збіжності: ознаки порівняння, граничну ознаку порівняння, ознаки Даламбера і Коші, інтегральну ознаку Коші. Для яких рядів застосовні ці ознаки?

5. Сформулювати і довести ознаку Лейбніца, Для якого ряду застосовна ця ознака?

6. У чому полягає наслідок з теореми Лебніца?

7. Сформулювати і довести достатню ознаку збіжності знакозмінного ряду.

8. Який ряд називається абсолютно збіжним? Який ряд називається умовно збіжним? Навести приклади.

Тема 7.2. Степеневі ряди

1. Який ряд називається функціональним? Що називається областю його збіжності?

2. Який ряд називається степеневим? Сформулювати і довести теорему Абеля.

3. Сформулювати і довести властивості степеневих рядів.

4. Що називається рядом Тейлора для функції 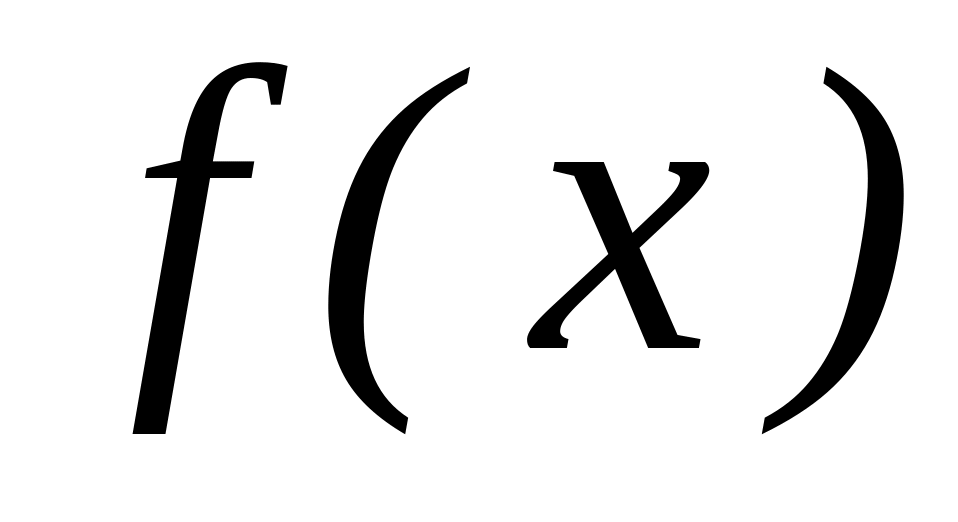. Як знайти коефіцієнти ряду Тейлора?

5. Який ряд називається рядом Маклорена?

6. Як наближено обчислити значення функції за допомогою степеневого ряду? Вказати способи оцінки залишку ряду. Навести приклади.

7. В чому полягає метод інтегрування функцій за допомогою рядів? Навести приклади.

8. У чому полягає метод інтегрування диференціальних рівнянь за допомогою рядів? Навести приклади.

ЛІТЕРАТУРА

1. Дубовик В.П., Юрик І.І. Вища математика. К: 2001.

2. Бугір М. Математика для економістів К: Академія, 1998.

3. Дубовик В.П., Юрик І.І. Вища математика. Збірник задач. К: 2001.

4. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. М: Наука, 1990.

5. Назієв Е.Х., Владіміров В.М., Миронець О.А. Лінійна алгебра та аналітична геометрія. К: Либідь, 1997.

6. Кремер Н.Ш. Высшая математика для экономистов.М: ЮНИТИ, 1998.

7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М: Высшая школа, 1986.

8. Скицько А.І. Лінійна алгебра та аналітична геометрія для

економістів. Чернівці: Золоті літаври, - 2003.

Теми курсу “Вища математика”

Лінійна алгебра

1. Матриці. Види матриць. Додавання матриць і множення матриці на число. Добуток матриць. Специфічні властивості матриць.

2. Визначники другого та третього порядків. Визначники n-го порядку.

3. Мінори та алгебраічні доповнення визначника.

4. Розклад визначника за елементами рядка або стовпця. Практичні способи обчислення визначників.

5. Поняття про обернену матрицю. Необхідна і достатня умови існування оберненої матриці. Знаходження оберненої матриці.

6. Ранг матриці. Теорема про ранг матриці.

7. Поняття про систему n-лінійних алгебраїчних рівнянь з m-невідомими. Умови сумісності і визначеності СЛАР.

8. Розв’язування систем n-рівнянь з m-невідомими. Теорема Кронекера-Капеллі.

9. Поняття про власні числа та власні значення матриць. Методи їх знаходження.

10. Поняття квадратичної форми. Закон інерції квадратичних форм. Приведення квадратичної форми до канонічного вигляду.

11. Застосування жорданових виключень до аналізу міжгалузевого балансу (стаціонарна модель Леонтьєва), лінійна модель обміну.