Тема 3.5. Основні теореми диференціального числення

1. Сформулювати і довести теореми Ферма і Ролля.

2. Сформулювати і довести теорему Коші.

3. Сформулювати і довести теорему Лагранжа. У чому полягає її геометричний і механічний зміст.

4. У чому суть правила Лопіталя? Довести відповідну теорему для розкриття невизн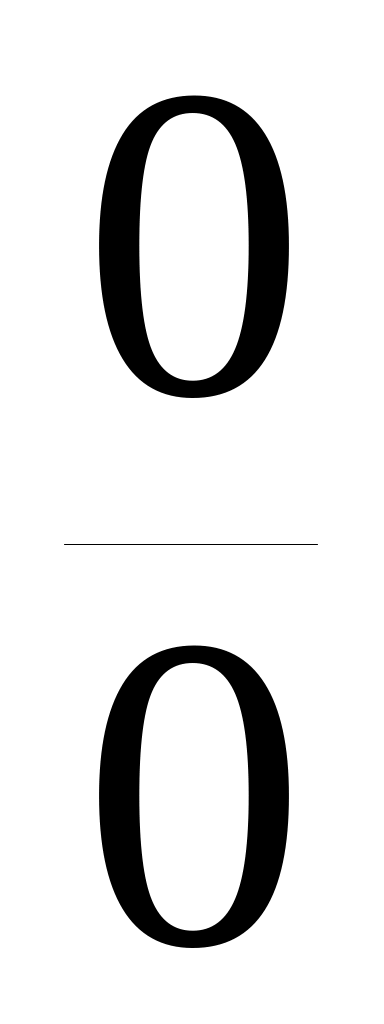аченості . Сформулювати теорему для випадку невизначеності 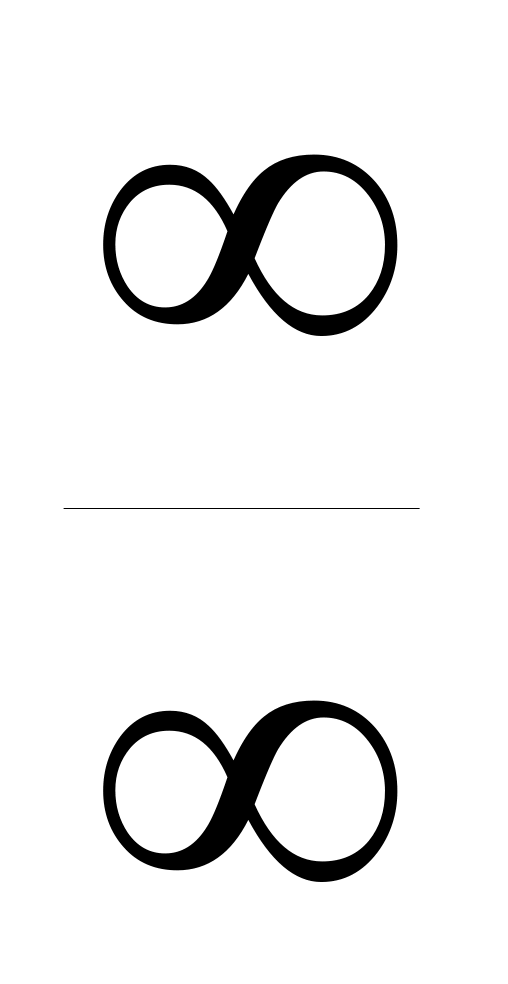. Навести приклади.

5. Як розкриваються невизначеності , , , , .

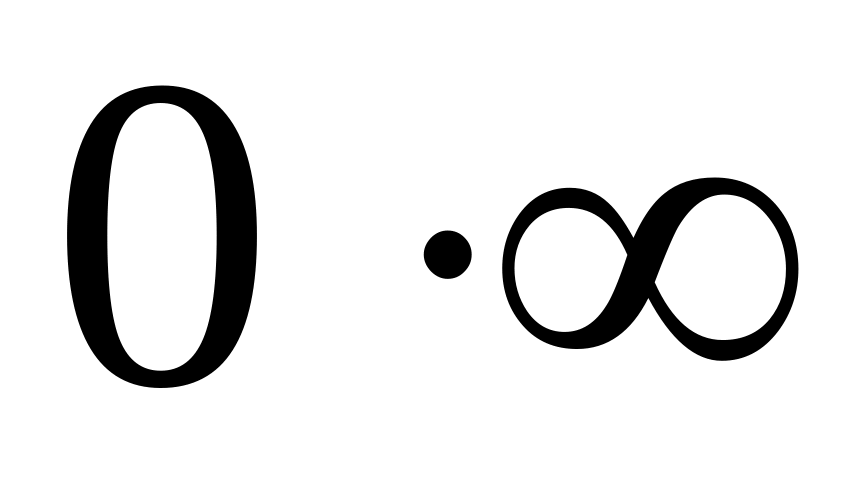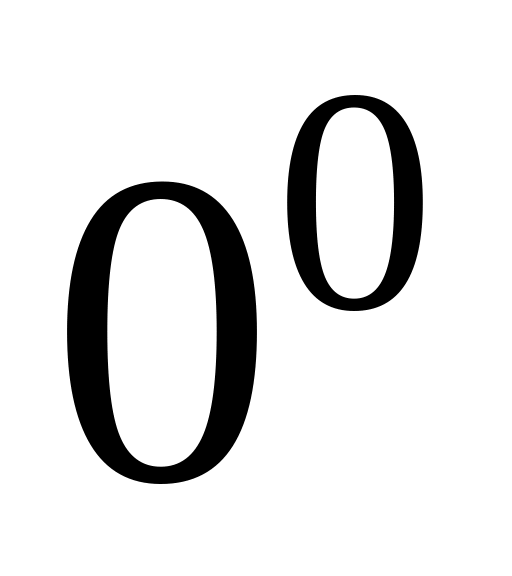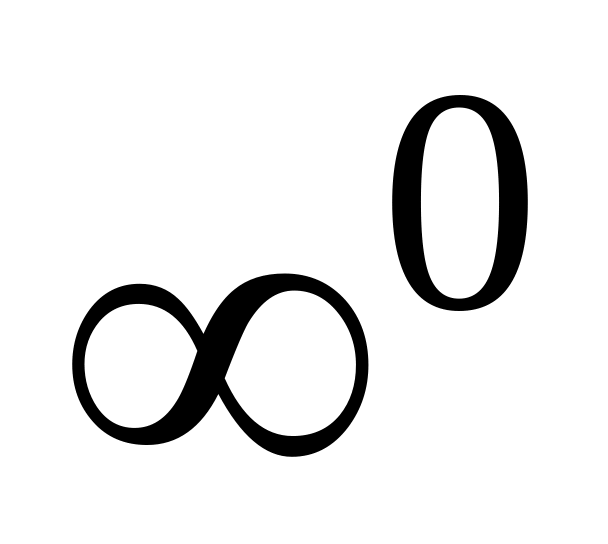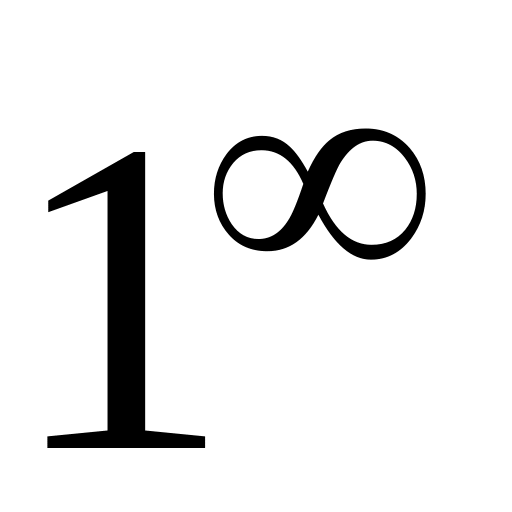Тема 3.6. Дослідження функцій за допомогою похідної

1. Сформулювати і довести умови строгої монотонності функції на інтервалі.

2. Які точки називаються стаціонарними?

3. В чому полягає правило знаходження інтервалів монотонності.?

4. Що називається точкою локального мінімуму та локальним мінімумом функції?

5. Що називається локальним екстремумом і чим він відрізняється від абсолютного екстремуму?

6. Сформулювати і довести необхідні умови локального екстремуму та першу і другу достатні умови.

7. У чому полягають правила знаходження екстремуму за першою, другою достатніми умовами? Навести приклади.

8. Як знайти найбільше і найменше значення функції на відрізку.

9. Яка крива називається опуклою (вгнутою) на інтервалі?

10. Що називається точкою перегину?

11. Які точки називаються критичними точками другого роду?

12. Чи довільна точка перегину є критичною точкою другого роду? А навпаки? Навести приклади.

13. Яка достатня умова того, що критична точка другого роду є абсцисою точки перегину? Навести приклади.

14. Сформулювати правило знаходження інтервалів опуклості, вгнутості та точок перегину.

15. Що називається асимптотою кривої?

16. Як знайти вертикальну асимптоту? Похилу асимптоту?

17. В чому полягає загальна схема дослідження функцій?

Розділ 4. Функції багатьох змінних (фбз) Тема 4.1. Функція, її границя та неперервність

1. Що називається функцією двох змінних?

2. Що називається областю визначення функції і який її геометричний зміст?

3. Що являє собою графік функції 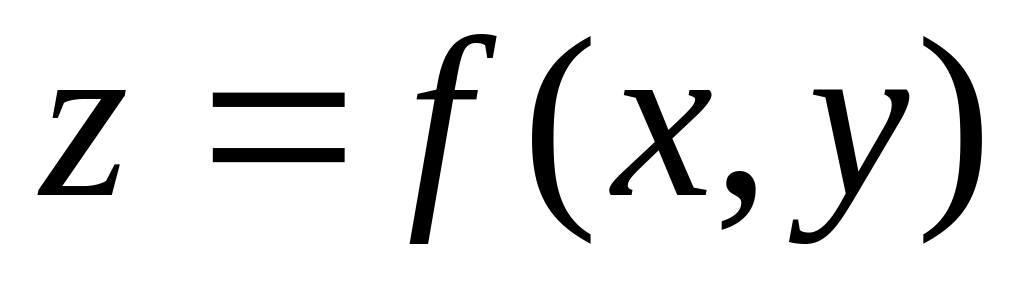? У чому полягає метод перерізів?

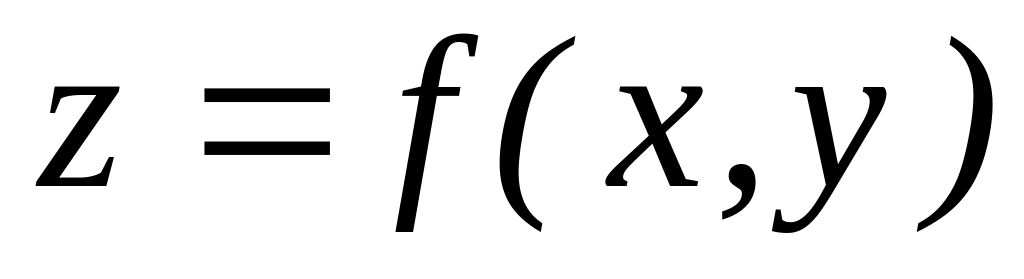4. Що називається лінією рівня функції . Навести приклади.

5. Дати означення функції трьох змінних, n змінних.

6. Що називається границею функції 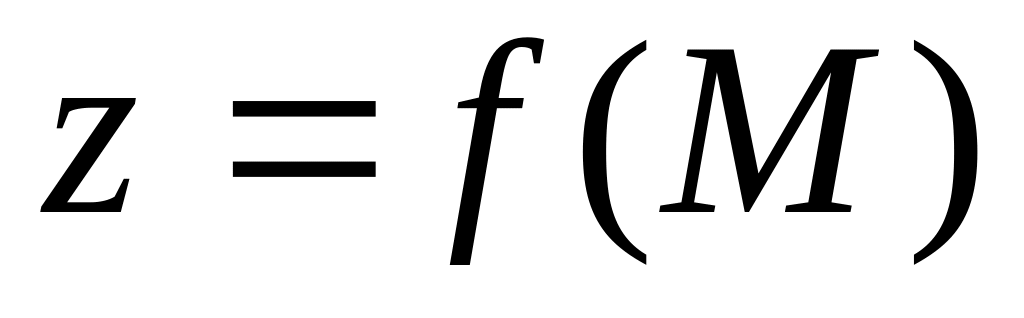при ?

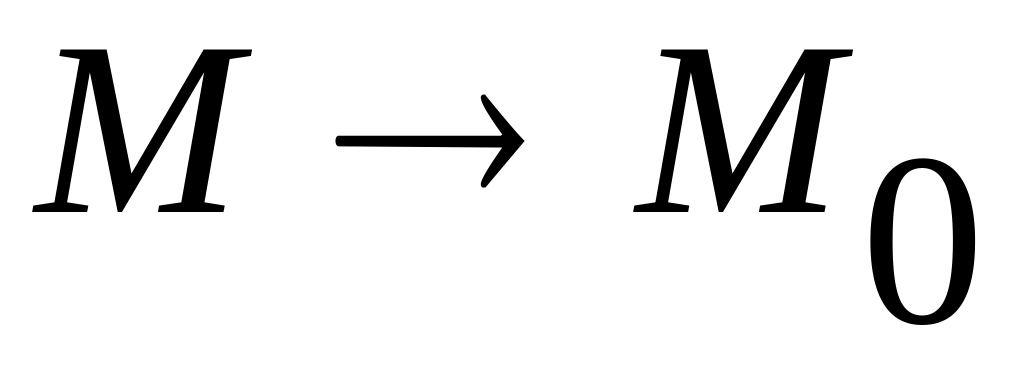7. Дати означення неперервної функції двох змінних в точці і на множині точок.

8. Що називається замкненою обмеженою областю?

Тема 4.2 Похідні та диференціали фбз

1. Дати означення частинної похідної функції двох змінних по одній з них. Зясувати її геометричний зміст.

2. Як визначаються частинні похідні другого і третього порядку від функції двох змінних?

3. Сформулювати теорему про рівність других мішаних похідних.

4. Дати означення диференційованості функції .

5. Довести теорему про неперервність диференційованої функції.

6. Довести теорему про існування частинних похідних диференційованої функції.

7. Вивести достатні умови диференційованості функції двох змінних.

8. Дати означення повного диференціалу функції двох змінних і вказати формули для його знаходження. Узагальнити цю формулу для функцій багатьох змінних.

9. Як застосовується повний диференціал функції для наближеного обчислення її значень?

10. Як знайти похідну складеної функції?

11. Що називається повною похідною?

12. У чому полягає інваріантність форми диференціалу першого порядку? Чому цієї властивості не мають диференціали вищих порядків?

13. Сформулювати теореми існування неявних функцій однієї і двох змінних і вивести правила диференціювання цих функцій.