Розділ 3 Диференціальне числення функції однієї змінної Тема 3.1. Функція

1. Що називається функцією? Навести приклади.

2. Що називається областю визначення та множиною значень функції?

3. Охарактеризувати основні способи задання функції.

4. Які функції називаються основними елементарними функціями?

5. Яка функція називається складеною? Навести приклади.

6. Яка функція називається парною, непарною? Які особливості цих функцій? Навести приклади.

7. Яка функція називається періодичною? Що називається її основним періодом? Навести приклади.

8. Як знайти функцію обернену до даної? За яких умов існує обернена функція? Навести приклади.

9. Яка функція називається неявно заданою, параметрично заданою?

Тема 3.2. Границя функції

1. Що називається числовою послідовністю і як її можна задати? Навести приклади.

2. Що називається границею числової послідовності? Який геометричний зміст границі?

3. Довести, що коли змінна величина має границю, то ця границя лише одна.

4. Довести, що границя сталої величини дорівнює цій сталій.

5. Яка величина називається нескінченно великою? Сформулювати властивості нескінченно великих величин.

6. Дати означення границі функції в точці на ’’мові послідовностей’’ і на мові .

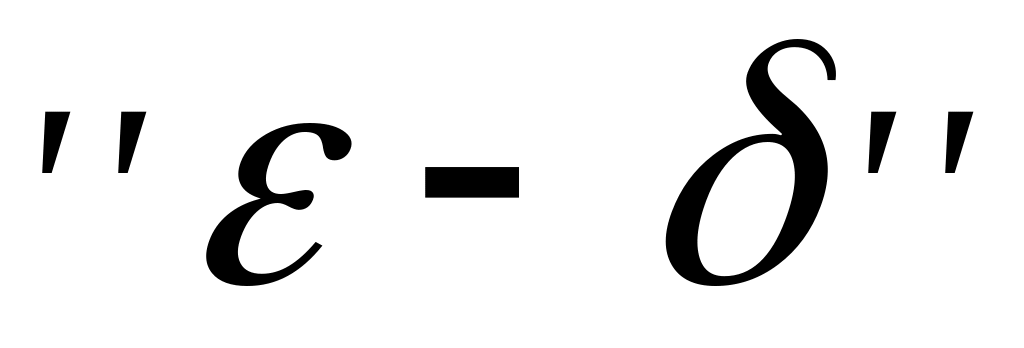7. У чому поляга геометричний зміст границі функції в точці? Навести приклади.

8. Що називається лівою границею функції в точці?

9. Що називається правою границею функції в точці?

10. Що називається границею функції при ?

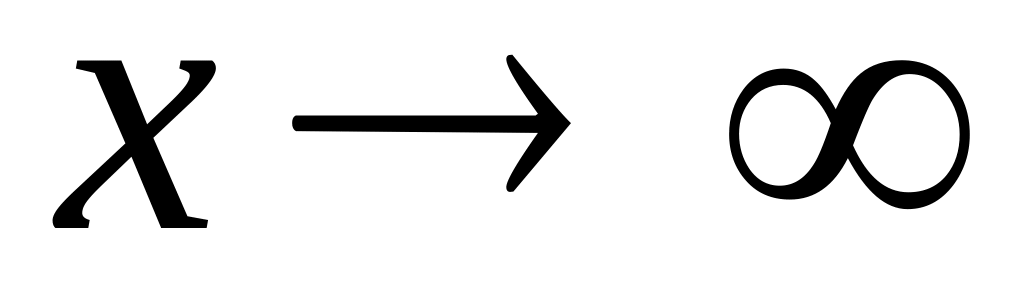11. Що називається нескінченно великою функцією?

12. Які величини називаються нескінченно малими? Сформулювати і довести властивості нескінченно малих.

13. Як порівнюються між собою нескінченно малі величини?

14. Які нескінченно малі величини називаються еквівалентними?

15. Сформулювати і довести теореми про границю суми, добутку, і частки, про границю проміжної функції; про граничний перехід в функціях.

Тема 3.3. Неперервність функцій

1. Дати означення неперервності функції в точці; а) через односторонні границі; б) через прирости функції і аргументу.

2. Який розрив називається: а) розривом першого роду; розривом другого роду? Навести приклади.

3. Який розрив називається усувним. Навести приклади.

4. Довести, що функція 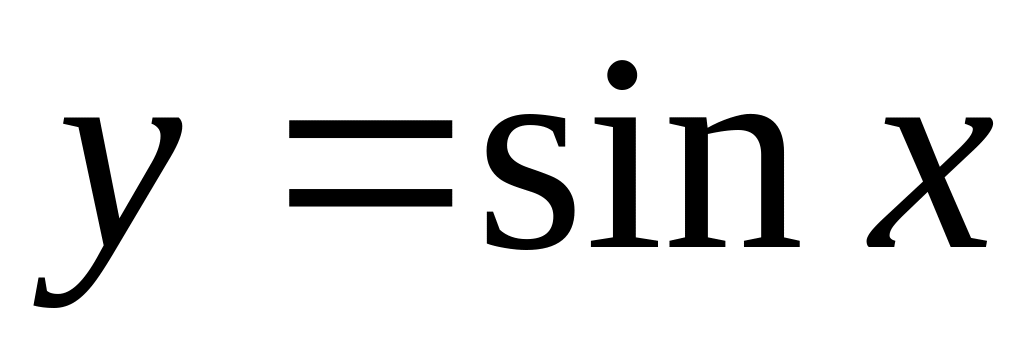неперервна на всій числовій осі.

5. Сформулювати і довести теорему про неперервність в точці елементарних функцій.

6. Яка функція називається неперервною на проміжку?

7. Сформулювати теореми про властивості функцій, неперервних на відрізку. Який геометричний зміст цих теорем?

Тема 3.4. Похідна та диференціал функції

1. Дати означення похідної заданої функції.

2. Який геометричний, механічний, економічний зміст похідної.

3. Як знайти похідну, виходячи з її означення?

4. Вивести рівняння дотичної і нормалі до кривої в заданій точці.

5. Як визначається кут між кривими?

6. Дати означення диференційованості функції в точці і на проміжку.

7. Який клас функцій ширший: неперервних в точці, чи диференційованих в точці? Навести приклади.

8. Вивести правила диференціювання суми, різниці, добутку і частки двох функцій. Навести приклади.

9. Вивести правило диференціювання складеної функції. Навести приклади.

10. Вивести правило диференціювання оберненої функції.

11. Вивести правило диференціювання параметрично заданої функції. Навести приклади.

12. Як диференціювати неявно задану функцію7 навести приклади.

13. У чому суть логарифмічного диференціювання. Навести приклади.

14. Що називається диференціалом функції? Як визначається диференціал функції через її похідну?

15. Який геометричний та механічний зміст диференціалу?

16. Назвати властивості диференціала. У чому полягає інваріантність форми диференціала?

17. Обґрунтувати формулу для наближеного обчислення значення функції за допомогою диференціала?