БУКОВИНСЬКИЙ ДЕРЖАВНИЙ

ФІНАНСОВО-ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ

Кафедра вищої математики

Питання

для самостійної роботи студентів з курсу

”Вища математика”

Розробив:

к.ф.-м.н., доцент Скицько А.І.

Розділ 1. Лінійна алгебра Тема 1.1. Матриці, дії над матрицями

1. Що називається матрицею ?

2. Як визначаються : сума двох матриць, добуток матриці на число, різниця та добуток двох матриць? Властивості цих дій.

3. Що називається оберненою матрицею?

4. Сформулювати і довести теорему про існування оберненої матриці. Алгоритм побудови оберненої матриці.

5. Що називається рангом матриці? Як знаходиться ранг матриці?

6. Які перетворення над матрицею називаються елементарними?

Тема 1.2. Визначники n-го порядку. Властивості визначників

1. Що називається визначником другого порядку?

2. Що називається визначником третього порядку?

3. Сформулювати основні властивості визначників.

4. Що називається мінором і алгебраїчним доповненням?

5. Сформулювати теорему про розклад визначника за елементами рядка (стовпця). Чому дорівнює сума добутків елементів одного рядка (стовпця) на відповідні алгебраїчні доповнення іншого рядка (стовпця).

6. Дати означення визначника n-го порядку.

7. Як обчислюється визначники вищих порядків?

Тема 1.3. Системи лінійних алгебраїчних рівнянь (слар)

1. Що називається системою m лінійних алгебраїчних рівнянь з n невідомими?

2. Яка система лінійних рівнянь називається : сумісною, несумісною, визначеною, невизначеною?

3. Записати формули Крамера. В якому випадку вони застосовуються? Довести формули Крамера для системи трьох рівнянь з трьома невідомими.

4. В чому полягає метод розв’язку СЛАР методом оберненої матриці?

5. У чому полягає метод Гаусса?

6. За яких умов однорідна система лінійних рівнянь має єдиний нульовий розв’язок; безліч розв’язків?

7. Сформулюйте теорему Кронекера-Капеллі, теореми сумісних систем.

Тема 1.4. Застосування лінійної алгебри до економічних задач

1. Застосування лінійної алгебри до аналізу міжгалузевого балансу (стаціонарна модель Леотьєва), лінійні моделі обміну.

Розділ 2 Аналітична геометрія

Тема 2.1. Лінійні операції над векторами

1. Що називається вектором, ортом, нульовим вектором? Що називається довжиною вектора?

2. Які вектори називаються рівними, колінеарними, компланарними?

3. Як визначається сума двох векторів, сума кількох векторів, різниця двох векторів, добуток вектора на число?

4. Сформулюйте властивості лінійних операцій над векторами.

5. Дати поняття N-вимірного вектора і N-вимірного простору.

6. Що називається лінійною комбінацією системи векторів? Яка лінійна комбінація називається тривіальною?

7. Сформулюйте означення лінійно залежної і лінійно незалежної системи векторів. Які необхідні і достатні умови лінійної залежності системи векторів?

8. Що називається базисом системи векторів? Як виразити вектори даної системи векторів через вектори базису?

9. Як виконуються операції над векторами, заданими своїми координатами в деякому базисі?

Тема 2.2 Системи координат

1. Що таке прямокутна декартова система координат у просторі? Яка система координат називається правою, лівою?

2. Запишіть формули розкладання по осях прямокутної декартової системи координат довільного вектора і радіуса вектора точки .

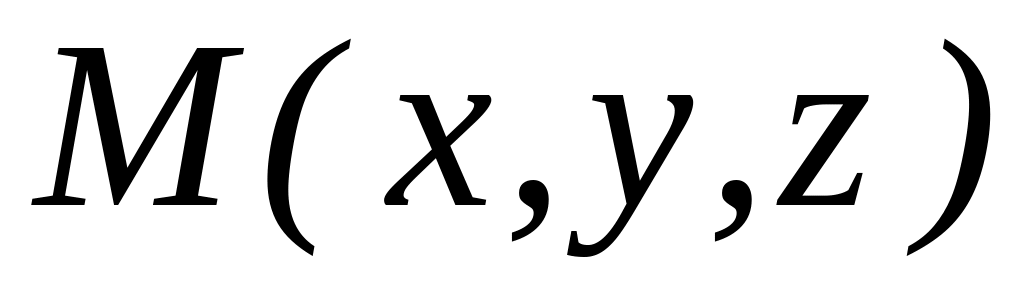3. Запишіть формули за якими обчислюються у прямокутних декартових координатах модуль, проекції на координатні осі та напрямні косинуси вектора. Чому дорівнюють проекції на координатні осі вектора, заданого координатами його початку й кінця?

4. Запишіть формулу, за якою знаходимо відстань між двома точками.

5. Запишіть формули поділу відрізка у даному відношенні.