
- •221400 «Управление качеством»
- •Содержание п редисловие
- •Задание 1.
- •1.1 Предпосылки расчета
- •1.1 Предпосылки расчета
- •Задание 2 Способы назначения и обработки оценок весомости Краткие теоретические сведения
- •1. Требования к бальным оценкам
- •2. Способ вспомогательной шкалы
- •3. Способ парных сравнений
- •4. Стоимостной способ
- •4.1. Область применения способа
- •4.2. Особенности работы со стоимостными оценками
- •5. Использование статистического критерия d'
- •5.1 Проверка выпадения одной экстремальной оценки
- •5.2 Проверка выпадения двух односторонних экстремальных оценок (критерий d'')
- •5.3 Проверка выпадения двух разносторонних экстремальных оценок.
- •Рекомендуемая литература
- •221400 «Управление качеством»
2. Способ вспомогательной шкалы
Вспомогательная шкала, предназначенная для назначения оценок весомости представляет собой совокупность качественных (словесных) описаний, которые в обобщённой форме характеризуют значимость показателя с точки зрения его влияния на качество оцениваемого объекта или же значимость фактора (объекта) относительно сопоставляемых с ним (далее для краткости будем писать только «показателя», имея в виду и другие значения). Обычно вспомогательную шкалу строят, симметричной.
Например:
Характеристики значимости |
Баллы |
Крайне важный показатель |
+4 |
Важный показатель |
+2 |
Показатель средней важности |
0 |
Маловажный показатель |
-2 |
Крайне маловажный показатель |
-4 |
В психофизиологии показано, что симметричные шкалы удовлетворительно обеспечивают равенство «расстояний» между объектами с одинаковой разницей баллов. Межэкспертную согласованность оценок считают достаточной, если максимальное расхождение оценок одного показателя разными экспертами не превышает 20% диапазона шкалы.
Трудности возникают с контрольной операцией. Как правило, ее можно выполнить лишь через некоторое время, порядка недели, когда эксперт забудет ранее назначенные им оценки. Иногда удается организовать проверку, предлагая эксперту поставлять по важности один оцениваемый объект с суммой других и сравнивая результаты этого сопоставления с результатом, полученным путем суммирования ранее поставленных бальных оценок. Воспроизводимость считают удовлетворительной, если оценки показателя, полученные в разное время, расходятся не более, чем на 20% от диапазона шкалы.
Симметричную вспомогательную шкалу удобно использовать при назначении оценок. Но при обработке, как правило, переходят к несимметричной положительной шкале, прибавляя ко всем назначенным оценкам наивысший балл (4 балла в нашем примере).
При расчете окончательных оценок они могут быть нормированы к 1, 10 или 100 путем деления обобщенной оценки каждого показателя на их сумму и умножения на соответствующее из указанных чисел. Если обобщенная нормированная оценка какого-либо показателя оказывается меньше 0,1 от максимальной, то этот показатель исключают, а оценки остальных - пересчитывают.
3. Способ парных сравнений
Способ парных сравнений имеет несколько модификаций. Наиболее часто применяют следующую.
1) Берут показатели одной группы, подлежащие оцениванию.
2) На бумаге строят таблицу размерностью n*(n-l), где п - число показателей в группе. По левой и верхней сторонам таблицы заносят названия (или просто номера) показателей. Удобно записывать первым наиболее значимый, по предварительному суждению эксперта, показатель и далее - по убыванию значимости. Такое расположение облегчает проверку внутренней непротиворечивости индивидуальных оценок эксперта, ибо числа в каждой строке должны монотонно убывать слева направо. Если они возрастают, то оценки эксперта внутренне противоречивы.
3) Наиболее значимый показатель оценивают в 10 баллов. Сравнивая его со вторым показателем, последнему проставляют в первой строке (в ячейке (1, 2)) оценку в 6аллах, соответствующую его значимости, например, 6 баллов. После этого первый показатель сравнивают с третьим и т.д.. Закончив заполнение первой строки, таким же способом заполняют вторую, принимая на этот раз весомость второго показателя в 10 баллов и т.д.
Приведем пример индивидуально заполненной экспертом матрицы парных сравнений для группы показателей составляющих группу отказов направляющего аппарата электроцентробежного насоса (таблица 4).
Таблица 4
Показатели (вид отказа) |
Сравниваемые показатели |
|||
(2) |
(3) |
(4) |
(5) |
|
(1)Износ расточки ступицы |
6 |
4 |
3(2,5) |
2(1,5) |
(2) Износ нижнего подпятника |
Х |
8 |
4 |
2 |
(3)Гидроабразивный износ лопастей |
|
Х |
5 |
3 |
(4) Износ верхнего подпятника |
|
|
Х |
6 |
(5) Износ внутренней поверхности чашки |
|
|
|
Х |
Примечание. Числа в скобках - после уточнения |
||||
Как видно из описания способа, контрольная операция состоит в том, что при сопоставлении значимости каждого показателя с каждым, появляется возможность несколькими путями рассчитать оценки значимости показателей и затем сопоставить полученные оценки между собой.
Обработка состоит в следующем:
1) вычисляют относительные оценки весомости каждого показателя не менее чем двумя путями;
2) если относительные оценки весомости некоторого показателя у одного эксперта, полученные различными путями, расходятся больше чем на 20%, то проводят повторный опрос эксперта, указывая ему на обнаруженное несоответствие.
3) если относительные оценки весомости одного и того же показателя у разных экспертов расходятся более чем на 20% проводят обсуждение расхождений и корректируют индивидуальные оценки;
4) если оценки весомости согласованы. вычисляют среднее значение по всем экспертам, что и дает окончательную оценку весомости. Далее окончательные оценки могут быть нормированы (см. п. 2).
Проиллюстрируем способ коррекции расхождений. Используем представленную выше индивидуально заполненную матрицу. Здесь отношение весомостей показателей следующее:
Таблица 5
По строке |
(2):(1) |
(3):(2) |
(4):(3) |
(5):(4) |
(1) |
0,6 |
0,67 |
0,75(0,63) |
0,67(0,6) |
(2) |
|
0,8 |
0,5 |
0,5 |
(3) |
|
|
0,5 |
0,6 |
(4) |
|
|
|
0,6 |
Как видно, только для соотношения (4):(3) имеет место допустимое расхождение (так как 0,75 - 0,5 > 0,2). Допустим, после указания на это расхождение эксперт поставил в ячейке (1, 4) значение 2,5 балла и, чтобы не изменилось соотношение 4-го и 5-го показателей, в ячейке (1,5) - 1,5 балла (числа в скобках в таблице 4). Тогда получаем внутренние согласованные оценки (числа в скобках в таблице 5) и рассчитываем индивидуальные нормированные коэффициенты весомости:
Весомость 2-го показателя определена относительно 1-го единственным способом:

Весомость
3-го показателя относительно 1-го можно
определить двумя способами: непосредственно
 и через 2-ой показатель
и через 2-ой показатель 
Среднее

Весомость 4-го показателя относительно 1-го определяют непосредственно, а также по цепочке- через 2-й и 3-й:



Среднее
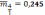
Наконец, весомость 5-го показателя также найдем путями:


Среднее

Если хотим нормировать весомость к единице, рассчитываем нормированные оценки по формуле

Выполнив подсчеты, находим:
 ;
;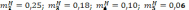
Поскольку весомость последнего показателя меньше 0,1, то показатель исключаем.
