
- •221400 «Управление качеством»
- •Содержание п редисловие
- •Задание 1.
- •1.1 Предпосылки расчета
- •1.1 Предпосылки расчета
- •Задание 2 Способы назначения и обработки оценок весомости Краткие теоретические сведения
- •1. Требования к бальным оценкам
- •2. Способ вспомогательной шкалы
- •3. Способ парных сравнений
- •4. Стоимостной способ
- •4.1. Область применения способа
- •4.2. Особенности работы со стоимостными оценками
- •5. Использование статистического критерия d'
- •5.1 Проверка выпадения одной экстремальной оценки
- •5.2 Проверка выпадения двух односторонних экстремальных оценок (критерий d'')
- •5.3 Проверка выпадения двух разносторонних экстремальных оценок.
- •Рекомендуемая литература
- •221400 «Управление качеством»
Приступая
к разработке методики оценивают качества
какого-либо объекта. вначале выполняют
опрос экспертов, направленный на
выявление максимальногочисла данных,
с использованием которых будет построена
методика. то сеть «генерацию» исходного
массива данных.
Под
данными» (или «предложениями» Понимают
ту совокупность однородных сведений,
которые должен представить эксперт в
результате опроса согласно цели
экспертизы. Это могут быть: показатели
свойств, составляющих качество объекта
оценивания: внешние факторы, влияющие
на качество; возможные решения в
отношении объекта оценивания и т.п.
Именно
на начальном этапе необходимо хотя бы
приблизительно оценить число экспертов,
которые должны быть опрошены, чтобы с
достаточной полнотой были выявлены
требуемые для решения квалиметрической
задачи данные.
Иногда
считаю, чтотакая оценка невозможна,
так как каждый следующий привлекаемый
эксперт может внести хотя бы одно новое
предложение, т.е. число возможных
предложений не ограничено. А потому и
не может стоять вопрос о полноте их
выявления.
Однако
это суждение неверно. Специально
проведенные опыты. направленные на
генерацию данных, показали, что с
Привлечением
каждого следующего эксперта вероятность
по- явления нового предложения тем
меньше, чем больше число уже имеющихся
данных. Именно
этот экспериментальный факт позволяет
обосновать способ определения числа
экспертов
оценивания
количества не выявленных данных.
Для
обоснования способа расчета допустим,
что все потенциальные эксперты примерно
одинаково продуктивны, облада-1.1 Предпосылки расчета
1.1 Предпосылки расчета
Краткие
теоретические сведения
Приступая
к разработке методики оценивают качества
какого-либо объекта. вначале выполняют
опрос экспертов, направленный на
выявление максимальногочисла данных,
с использованием которых будет построена
методика. то сеть «генерацию» исходного
массива данных.
Под
данными» (или «предложениями» Понимают
ту совокупность однородных сведений,
которые должен представить эксперт в
результате опроса согласно цели
экспертизы. Это могут быть: показатели
свойств, составляющих качество объекта
оценивания: внешние факторы, влияющие
на качество; возможные решения в
отношении объекта оценивания и т.п.
Именно
на начальном этапе необходимо хотя бы
приблизительно оценить число экспертов,
которые должны быть опрошены, чтобы с
достаточной полнотой были выявлены
требуемые для решения квалиметрической
задачи данные.
Иногда
считаю, чтотакая оценка невозможна,
так как каждый следующий привлекаемый
эксперт может внести хотя бы одно новое
предложение, т.е. число возможных
предложений не ограничено. А потому и
не может стоять вопрос о полноте их
выявления.
Однако
это суждение неверно. Специально
проведенные опыты. направленные на
генерацию данных, показали, что с
Привлечением
каждого следующего эксперта вероятность
по- явления нового предложения тем
меньше, чем больше число уже имеющихся
данных. Именно
этот экспериментальный факт позволяет
обосновать способ определения числа
экспертов
оценивания
количества не выявленных данных.
Для
обоснования способа расчета допустим,
что все потенциальные эксперты примерно
одинаково продуктивны, облада-
В связи с этим на начальном этапе любой экспертизы основной задачей квалиметролога является грамотное формирование экспертной группы, в ходе которого определяется оптимальное количество экспертов, необходимое для проведения экспертизы, а также проводится количественная оценка качества экспертной группы различными методами.
Расчёт числа экспертов, необходимого для выявления наиболее полного количества данных, сводится к нахождению такого их числа m, при котором вероятность появления содержательно нового предложения с привлечением (m + 1)-го эксперта становится меньше заранее принятого значения a.
Для решения поставленной задачи используют следующий алгоритм:
1. Проводят опрос экспертов с целью получения совокупности сведений, касающихся объекта экспертизы.
2. Все предложения экспертов разделяют на четыре группы:
1) очевидные – выдвинутые всеми или почти всеми экспертами; 2) редкие – выдвинутые двумя (или тремя) экспертами; 3) новые – выдвинутые одним экспертом. Интерес представляют только редкие и новые предложения, базирующиеся на личном опыте экспертов, их способностях, интуиции. При этом вероятность появления особых предложений, выдвинутых меньшинством в группе из m экспертов, определяется выражением:
Pm
= (1)
(1)
где
 - количество новых предложений;
- количество новых предложений;
 редких
предложений, выдвинутых меньшинством
v.
редких
предложений, выдвинутых меньшинством
v.
3.
Из
группы в m
экспертов
образуют всевозможные подгруппы по (m
–
1) экспертов
и для каждой из них подсчитывают число
новых  и редких
и редких  предложений.
предложений.
4. Рассчитывают вероятность Pm-1 появления новых предложений
по всем подгруппам и коэффициент λ уменьшения вероятности появления новых предложений с переходом от (m -1) экспертов к m экспертам:
Pm-1
=  (2)
(2)
λ
=  (3)
(3)
5. При условии, что значение l сохраняется с увеличением числа экспертов (хотя, как правило, оно при этом уменьшается), оценки вероятности появления особых предложений с привлечением (m + 1)-го, (m + 2)-го… (m + k)-го экспертов будут соответственно равны:
Pm+1 = Pm·λ ; (4)
Pm+2 = Pm·λ2 (5)
…
Pm+k = Pm·λk (6)
Используя
выражение (3) и заданное значение
вероятности α, находят число k
вновь
привлекаемых экспертов, при котором
Pm+k
=
Pm·λk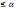 .
Окончательная формула для расчёта k
примет
вид.
.
Окончательная формула для расчёта k
примет
вид.
k
=  (7)
(7)
Следует отметить, что все допущения рассмотренного способа решения ориентированы на расчёт «с запасом». То есть, считая всех экспертов одинаково продуктивными, мы заведомо шли на завышение требуемого количества экспертов. В действительности (при правильно проведённом отборе экспертов) вначале в экспертную группу попадают наиболее сведущие специалисты, которые представляют максимальную информацию.
Привлекаемые далее эксперты менее продуктивны уже потому, что область этих профессиональных интересов удаляется от цели проведения экспертизы. Это приводит к уменьшению λ.
Так как рассмотренный вариант решения даёт завышенный объём экспертной группы, превышать рассчитанное количество экспертов не целесообразно. Главное – подробно опросить каждого эксперта, выявить наиболее полно его суждения и рационально организовать обмен мнениями.
Пример.
При
анкетном опросе N =
5 специалистов
относительно путей повышения надёжности
изделия было получено  nредложений,
причем некоторые были выдвинуты
несколькими специалистами так, что
содержательно предложений оказалось
nредложений,
причем некоторые были выдвинуты
несколькими специалистами так, что
содержательно предложений оказалось
 (таблица 1).
(таблица 1).
Решение.
Рассмотрим схему выдвижения предложений 5-ю экспертами (таблица 1).
Таблица 1
Номера предложений |
Эксперты |
||||
1 |
2 |
3 |
4 |
5 |
|
1 |
+ |
+ |
+ |
+ |
+ |
2 |
+ |
+ |
+ |
+ |
+ Очевидные |
3 |
+ |
+ |
|
+ |
+ |
4 |
+ |
|
+ |
+ |
|
5 |
|
|
+ |
+ |
Редкие |
6 |
|
+ |
+ |
|
|
7 |
+ |
+ |
|
|
|
8 |
|
+ |
|
|
Новые |
9 |
|
|
|
|
+ |
10 |
+ |
|
|
|
|
Общее число предложений от всех экспертов M5 = 26. Число предложений по количеству выдвинувших их экспepтoв следующее:
 =3;
=3;
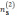 =3;
=3;
 =1;
=1;
 =1;
=1;
 =2
=2
Как можно видеть существуют предложения, выдвинутые всеми или многими экспертами, - «очевидные». Эти предложения для расчета не используем, т.к. ясно, что их будет выдвигать почти каждый из вновь привлекаемых экспертов.
С позиции выявления новых данных важны только предложения, выдвинутые одним и двумя экспертами каждое, - «новые» и «редкие». Эти предложения базируются на личном опыте, интуиции и размышлениях каждого эксперта. Именно такие предложения существенны при привлечении следующих экспертов.
Допустим, привлечен (m+1)-й эксперт, который привносит, в среднем, то же число данных, что и каждый из предыдущих. Насколько вырастет число «новых» данных? Как характеризовать увеличение числa различных по существу данных, учитывая, что большая часть того, что мог бы предложить(m+ l)-й эксперт уже предложено? Сколько еще следует опросить экспертов, чтобы вероятность р появления новых данных стала достаточно малой?
Решение
этой задачи базируется на оценке по
опытным данным величины  ,
которая показывает, во сколько раз
уменьшается вероятность появления
новых предложений с привлечением в
группу очередного эксперта.
,
которая показывает, во сколько раз
уменьшается вероятность появления
новых предложений с привлечением в
группу очередного эксперта.
Остается
найти К
-
такое число новых привлекаемых экспертов.
При котором РN+к
становится
достаточно малой величиной, меньше
некоторогокритического значения  .
Значение
выбирают
в зависимости от ответственности
решаемой задачи, - от 0,1 до 0,01. Таким
образом, число вновь привлекаемыхэкспертов
находим из условия:
.
Значение
выбирают
в зависимости от ответственности
решаемой задачи, - от 0,1 до 0,01. Таким
образом, число вновь привлекаемыхэкспертов
находим из условия: и по одному предложению, выдвинутому
тремя и четырьмя экспертами
и по одному предложению, выдвинутому
тремя и четырьмя экспертами 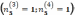 .
Итого, четыре «очевидных» предложения.
«Редких» предложений, каждое из которых
выдвинуто двумя экспертами, всего три
.
Итого, четыре «очевидных» предложения.
«Редких» предложений, каждое из которых
выдвинуто двумя экспертами, всего три
 .
Наконец «новых» предложений тоже
три
.
Наконец «новых» предложений тоже
три  .
.
Тогда
оценка вероятности появления нового
предложения для N=5 будет:
Тогда
оценка вероятности появления нового
предложения для N=5 будет:
Образуем теперь из группы в 5 экспертов всевозможные подгруппы по N - 1= 4 эксперта (этих подгрупп, естественно будет 5) и для каждой из них подсчитаем число редких и новых предложений. Нетрудно убедиться, что эти числа будут 6,2,4,6,6 и 3,4,5,4,2 и, следовательно, оценка вероятности появления новых предложений:
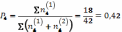
где суммирование происходит по всем образованным n группам. Отношение дает величину - коэффициент уменьшения вероятности появления новых данных при переходе от N - 1 =4 экспертов к N=5 экспертам:

Предположим,
что значение сохраняется с привлечением последующих
экспертов (заметим, что по данным разных
опытов значение
сохраняется с привлечением последующих
экспертов (заметим, что по данным разных
опытов значение  было
получено в пределах от 0,4 до 0,9.Тогда
вероятности появления новых сведений
с привлечением (m
+
1), (m
+
2), ..., (m
+
k)-гo
экспертов будут:
было
получено в пределах от 0,4 до 0,9.Тогда
вероятности появления новых сведений
с привлечением (m
+
1), (m
+
2), ..., (m
+
k)-гo
экспертов будут:
 ;
Pm+k
=
Pm·λk
;
Pm+k
=
Pm·λk
Или, для данных настоящего примера:
 .
.
Остается
найти К
-
такое число новых привлекаемых экспертов.
При котором Рm+k
становится
достаточно малой величиной, меньше
некоторого критического значения
.
Значение  выбирают
в зависимости от ответственности
решаемой задачи, от 0,1 до 0,01. Таким
образом, число вновь привлекаемых
экспертов находим из условия:
выбирают
в зависимости от ответственности
решаемой задачи, от 0,1 до 0,01. Таким
образом, число вновь привлекаемых
экспертов находим из условия:
Pm+k = Pm·λk .
Приняв α= 0,01, имеем:

Итак, для достижения поставленного условия следует привлечь к работе ещё 5 специалистов, или всего 10 человек, которых следует опросить для достижения достаточной уверенности в полноте выявления требуемых данных. Надо отметить, что по данным проведенных опытов, величина λ обычно убывает с ростом числа экспертов, а поэтому изложенный способ расчета дает требуемое число с некоторым «запасом».
Какое же число предложений будет получено после опроса найденного количества экспертов и какое число предложений окажется не выявленным?
В
момент начала расчетов, когда опрошено
m
экспертов,
число выявленных и содержательно
различных данных равно  .
При этом оценка вероятности появления:
новых данных равна
.
При этом оценка вероятности появления:
новых данных равна  .
Коэффициент уменьшения вероятности
появления новых данных при привлечении
нового эксперта:
.
Коэффициент уменьшения вероятности
появления новых данных при привлечении
нового эксперта:

Тогда
среднее число новых предложений,
получаемых от (m
+
1)-гo эксперта будет  затем
(m
+
2)- го эксперта
затем
(m
+
2)- го эксперта 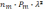 и т.д. Сумма m
+
k
членов
этой убывающей геометрической прогрессии
дает оценку общего числа предложений,
получаемых в результате опроса k
новых
экспертов:
и т.д. Сумма m
+
k
членов
этой убывающей геометрической прогрессии
дает оценку общего числа предложений,
получаемых в результате опроса k
новых
экспертов:

Для данных рассматриваемого примера, а именно, =10; = 0,33; = 0,79; k = 5 находим оценку общего числа новых предложений:

Предположим, что имеется возможность опросить неопределенно большое число экспертов. Тогда общее число ожидаемых новых предложений:

Таким образом, опрос десяти экспертов не исчерпывает возможности выявления содержательно новых данных. Количество экспертов необходимо увеличить.
Задание.
Имеется таблица представления данных 7 -ю эксперт.
(таблица 2).
Требуется:
а) определить количество экспертов (преподаватель вычёркивает одного - двух экспертов), которых следует дополнительно опросить, чтобы вероятность появления новых предложений оказалась не более α = 0,10; 0,05; 0,01 (преподаватель выбирает одно из значений α);
б) определить, сколько предложений при этом будет выявлено и сколько останется не выявленными.
Рекомендации преподавателю: вычеркнуть из таблицы 2 любых двух экспертов, кроме 7 и 8.
Таблица 2
Номера предложений |
Эксперты |
||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
|
+ |
+ |
+ |
+ |
+ |
+ |
2 |
+ |
+ |
+ |
+ |
|
+ |
+ |
3 |
+ |
+ |
+ |
|
+ |
|
|
4 |
|
+ |
+ |
+ |
+ |
|
|
5 |
+ |
|
|
+ |
|
|
|
6 |
|
+ |
|
|
+ |
|
|
7 |
|
|
+ |
|
|
+ |
|
8 |
|
|
|
+ |
|
|
+ |
9 |
+ |
|
|
|
|
+ |
|
10 |
|
+ |
|
|
|
|
|
11 |
|
|
+ |
|
|
|
|
12 |
|
|
|
+ |
|
|
|
13 |
|
|
|
|
+ |
|
|
14 |
|
|
|
|
|
|
+ |
