7.4. Дополнительные задачи и решения

Задача 7.1 .ДОП

Проектируемая мощность для ремонта двигателей в нашей компании равна 80 грузовиков / день. Эффективная мощность – 40 двигателей / день и текущий выход составляет 36 двигате­лей / день.

Коэффициент использования = Текущий выход /

/ Проектируемая мощность = 36 / 80 = 45 %.

Эффективность = Текущий выход /Эффективная мощность = 36 /40 = 90%. Нормативная мощность = (Проектируемая мощность) х

х (Коэффициент использования) х (Эффективность) =

= (80) (.45) (.90) = 32.4 двигателя / день.

Задача 7.2.ДОП

Нормативная мощность (ч / нед.) за последние шесть лет пока­зана в следующей таблице:

Год	Нормативная мощность, ч / нед.
1-й	115
2-й	120
3-й	118
4-й	124
5-й	123
6-й	130

Спрогнозируем мощность в седьмом году, используя уравне­ние регрессии.

Год	Перенумерованный год, х	Мощность, у	х2	ху
1-й	–2.5	115	6.25	–287.5
2-й	–1.5	120	2.25	–180
3-й	–.5	118	.25	–59
4-й	+.5	124	.25	+62
5-й	+1.5	123	2.25	+184.5
6-й	+2.5	130	6.25	+325
	Σ х = 0	Σ у = 730	Σ х2 = 17.5	Σ ху = 45

Задача 7.3.ДОП

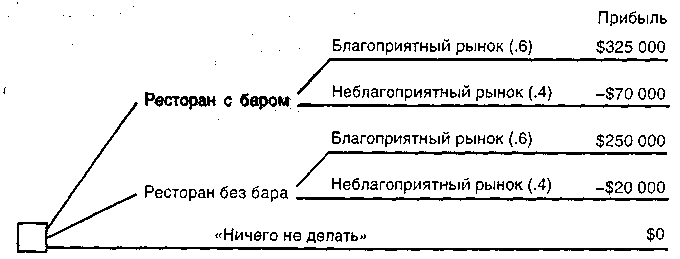
В качестве примера мы будем рассматривать строительство ресторана недалеко от университетского городка. Один из вари­антов включает открытие бара для продажи пива, тогда как другой план не предусматривает такую продажу. Шансы на успех со­ставляют .6 (шансы провала оцениваются как .4). Успех плана, включающего бар, оценивается прибылью $325000, а без бара прибыль будет $250000. Убытки для плана с баром – 70000, без бара – только $20000.

Дерево решений для рассматриваемого примера дано ниже.

ЕМV (1) = (.6) ($325000) + (.4) (–$70000) = $167000.

ЕМV (2) = (.6) ($250000) + (.4)( –$20000) = $142000.

ЕМV (3) = $0.

Выбрана альтернатива EMV (1), дающая наибольшее EMV. Решение принимается о строительстве ресторана с баром.

Задача 7.4.ДОП

F = $1000

V = $2

Р = $4

BEP($) =

BEP(x) = 500 шт.

Заметим, что безубыточность находится через разницу между продажной ценой и переменными затратами. Эта разница в при­мере равна $2 на штуку. Постоянные затраты составляют $1000 и, получая разницу от каждой штуки в размере $2, потребуется продать 500 штук и покрыть постоянные затраты. Эта концепция является главной в понимании затрат и ценообразования.

Задача 7.6.ДОП

Продолжим пример. Если мы инвестируем в банк $10 под 10 % годовых, тогда наши инвестиции будут $11 в первый год, и, если снова иметь добавленную стоимость $1.10 (10 % от $11, что экви­валентно .10 х $11 = $1.10) и, в общем, $12.10 ($1.10 + $11.00).

Чистая текущая стоимость показывает нам обратную арифметику. Например, если инвестиции будут произведены в размере $100 через два года относительно нынешнего, какова их стоимость сегодня при процентной ставке 10 %? Мы находим, что

текущая стоимость = будущая стоимость ($) х

х (значение фактора) = $100.000 х. 826 = $82.60.

Задача 7.7.ДОП

Мы вносим $6000 каждый год в течение пяти следующих лет. Какова текущая стоимость этих вкладов при ставке 10 %?

Значение фактора для 10 % и пяти лет = 3.79 (заметим, что 3.79 – это сумма .909 + .826 + .751 + .683 + .621).

Текущая стоимость = (3.79) х ($6000) = $22,740.