4.4. Дополнительные задачи и решения

Задача 4.1.ДОП

Скользящая средняя = ∑Спрос в предыдущие п периодов / п

Продажи велосипедов для фирмы показаны в средней колонке следующей таблицы. Трехнедельная средняя размещена в правой колонке.

Задача 4.2.ДОП

Взвешенная скользящая средняя = [∑ (Вес для периода n) *

* (Спрос в период п)] / ∑ Весов

Фирме требуется прогноз продаж велосипедов, взвешенный за три последние недели следующим образом:

Используемые веса	Период
3	Прошлая неделя
2	Две недели назад
1	Три недели назад

Трехнедельная взвешенная скользящая средняя помещена ниже.

Задача 4.3.Доп

Фирма использует простое экспоненциальное сглаживание с а = .1 для прогноза спроса. Прогноз для первой недели января был 500 единиц, тогда как текущий спрос в этот период оказался 450 единиц. Спрос для второй недели января считается следую­щим образом:

F_t = F_{t – 1} + а (A_{t – 1} – F_{t – 1}) = 500 +.1 (450 – 5500) = 495 ед.

Задача 4.4.ДОП

Фирма использует экспоненциальное сглаживание, прогнози­руя продажи автомобильных аккумуляторов. Рассматриваются две константы а, а = .8 и а - .5. Для определения точности прогноза с каждой константой мы должны рассчитать абсолютные отклоне­ния и MAD. Принимаемый прогноз для января был 22 аккумулятора.

Месяц	Текущие продажи аккумуляторов	Округленный прогноз (а = .8)	Абсолютное отклонение (а = .8)	Округленный прогноз (а = .5)	Абсолютное отклонение (а = .5)
Январь	20	22	2	22	2
Февраль	21	20	1	21	0
Март	15	21	6	21	6
Апрель	14	16	2	18	4
Май	13	.14	1	16	3
Июнь	16	13	3	15	1
Сумма абсолютных отклонений:			15		16

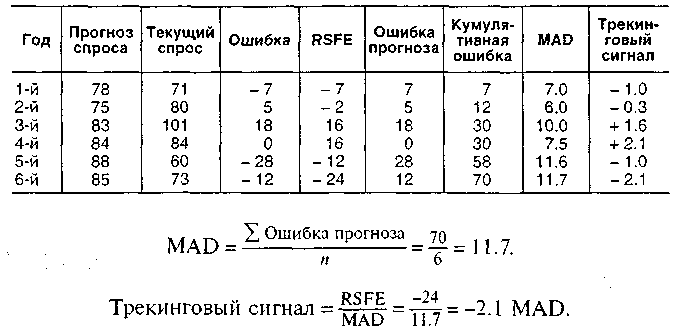
MAD = ∑ Отклонения / n ; 2.5 для а =.8; 2.7 для a =.5.

На основе этого анализа константа сглаживания а - .8 предпо­чтительнее a = .5, так как она дает меньшее MAD.

Задача 4.6.ДОП

Используя данные о продажах, приведенные ниже, опреде­лите:

а) уравнение регрессии методом наименьших квадратов;

б) объем продаж в 1993 г.

Год	Продажи, шт.
1986	100
1987	110
1988	122
1989	130
1990	139
1991	152
1992	164

Минимизируя расчеты, трансформируем значение х (время) в простейшее число. В этом случае 1986 г. будет значиться как год 1, 1987 г. – как год 2 и т. д.

Год	Временный период	Продажи, шт.	х2	ху
1986	1	100	1	100
1987	2	110	4	220
1988	3	122	9	366
1989	4	130	16	520
1990	5	139	25	695
1991	6	152	36	912
1992	1	100	49	1148
	Σ х = 28	Σ у =917	Σ х2 = 140	Σ ху = 3971

= = 28 / 7 = 4; = = 917 / 7 = 131;

b = = = 203 / 28 = 10.82,

а = – b = 131 – (10.82) (4) = 87.72.

Таким образом, уравнение регрессии имеет вид:

у = 87.72 + 10.82 х.

Проект спроса в 1993 г., т. е. году х= 8, определится так:

87.72 + 10.82 (8) = 174.28.

Задача 4.10.ДОП

Женщина-менеджер по сдаче внаем жилья считает, что спрос на квартиры может быть соотнесен с числом рекламных объявле­ний в газетах в течение прошлых месяцев. Она собрала данные, показанные в таблице ниже.

Наем жилья, у	Реклама в газетах, х
15	6
9	4
40	16
20	6
25	13
25	9
15	10
35	16

Мы можем найти математическое уравнение, используя метод наименьших квадратов.

Реклама, х	Наем, у	х2	ху
15	6	225	90
9	4	81	36
40	16	1600	640
20	6	400	120
25	13	625	325
25	9	625	225
15	10	225	150
35	16	1225	560
Σ х = 184	Σ у = 80	Σ х2 = 5006	Σ ху = 2146

= = 184 / 8 = 23; = = 80 / 8 = 10;

b = = = 0.395,

а = – b = (10 – (0.395) (23) = 0.91.

Таким образом, уравнение регрессии имеет вид:

у = .91 + .395 х

или

наем жилья = .91 + .395 реклама, помещенная в газете.

Если число реклам равно 30, мы можем определить число сданного жилья через уравнение регрессии:

.91 + .395 (30) = 13 квартир.

Задача 4.11 .ДОП

Используя данные о рекламе и сдаче жилья задачи 4.10.ДОП, рассчитайте стандартное отклонение уравнения регрессии (S_Y,_X).

4.12.ДОП

Для задачи 4.10.ДОП со следующими данными:

Σх = 184; ; Σх² = 5006; Σу = 80; Σy² = 950; Σху = 2146; n = 8 рассчитайте коэффициент корреляции.

Этот коэффициент r = .90 означает существенную корреляцию и подтверждает связь между двумя переменными: х и у.

Задача 4.14.ДОП

Прогноз спроса и текущий спрос на лодки показан в таблице ниже. По ней мы рассчитываем трекинговый сигнал и MAD.