Задача 4.17.Пк

По мнению угольной компании, спрос на уголь связан с индексом погодных условий, даваемых бюро погоды. Тогда, когда погода была наиболее холодной за последние пять лет (и индекс был высоким), продажи угля были высоки.

Хороший прогноз будущего годового спроса на уголь можно сделать на основе регрессионного уравнения, зная, каковы будут условия зимы следующего года. Для данных из следующей таб­лицы постройте регрессионное уравнение методом наименьших квадратов и рассчитайте коэффициент корреляции данных. Также рассчитайте стандартную ошибку прогноза.

Продажи угля, у, млн. т	Индекс погоды, х
4	2
1	1
4	4
6	5
5	3

Ответ 4.17: а =1.0; b =1.0; y = 1.0 + 1x; r =.845; S_УX = 1.15.

Задача 4.18.ПК

Тринадцать студентов обучались по П/ОМ-программе в уни­верситете два года назад. Следующая таблица показывает их сред­ний рейтинг (GPA) после программы двух лет и как были оценены знания каждого студента на экзаменах (SAT) за период обучения в высшей школе. Существует ли отношение между средним рей­тингом и оценками экзаменов? Если у студента значение SAT 350, что он думает о своем рейтинге? Каков рейтинг студента с SAT, равным 800?

Студент	Оценки (SAT)	Рейтинг (GPA)
А	421	2.90
В	377	2.93
С	585	3.00
D	690	3.45
Е	608	3.66
F	390	2.88
G	415	2.15
Н	481	2.53
I	729	3.22
J	501	1.99
К	613	2.75
L	709	3.90
М	366	1.60

Ответ 4.18: у = 0.972 + 0.0035*; r² = .479; х = 350, у = 2.191; х = 800, у = 3.77.

Задача 4.19.ПК

Доктор Росс – психиатр, специализирующийся на лечении пациентов, имеющих фобию и боящихся жить в своих домах. Следующая таблица показывает, скольких пациентов доктор Росс имел каждый год за последние десять лет.

Год	Число пациентов	Процент преступлений (грабежей на 1000 жителей)
1-й	36	58.3
2-й	33	61.1
3-й	40	73.4
4-й	41	75.7
5-й	40	81.1
6-й	55	89.0
7-й	60	101.1
8-й	54	94.8
9-й	58	103.3
10-й	61	116.2

Используя трендовый анализ, скажите, как много пациентов будет у доктора Росса в годах 11, 12, 13? Насколько хорошо эта модель подходит к данным?

Ответ 4.19: год 11 – 66 пациентов; год 12 – 69; год 13-72; r = .92.

Задача 4.20.ПК

Используя данные задачи 4.19, построить линейное уравнение регрессии для изучения соотношения между процентом преступ­лений и числом пациентов доктора Росса. Если процент грабежей вырастет до 131.2 в году 11, каким будет число пациентов? Если процент грабежей снизится до 90.6, какое число пациентов по­явится?

Ответ 4.20: 131.2 → 72.7 пациента; 90.6 → 50.6 пациента.

Задача 4.21

Бухгалтеры фирмы провели исследование 200 человек в про­шлом году и затем построили уравнение множественной регрес­сии, связывающее затраты на командировки сотрудника у с чис­лом дней поездки x₁ и расстоянием поездки в километрах х₂:

у= $90.00 + $48.50 x₁ + $.40 x₂.

Коэффициент корреляции был .68.

а) Если командированный уезжает за 300 километров и воз­вращается назад через пять дней, сколько денег он истратит?

б) Командированный попросил возместить ему сумму $685. Что должен сделать бухгалтер?

в) Могут ли быть включены другие переменные в уравнение? Если могут, то какие и почему?

Ответ 4.21: а) $452.50;

б) спросить его о расходах;

в) другие переменные должны быть вклю­чены, так как r = .68.

Задача 4.22

В прошлом дилер продавал в среднем 1000 единиц товара каждый год. В последние два года – соответственно 200 и 250, когда продажи были осенью, 300 и 350 – зимой, 150 и 165 – весной, 300 и 285 – летом. Дилер предполагает, что продажи в следующем году возрастут до 1200 единиц. Каков будет спрос в каждый сезон?

Ответ 4.22: осенью – 270; зимой – 390; весной – 189; летом – 351.

Задача 4.23.ПК

Пассажиро-мили для аэролинии показаны ниже для последних 12 недель.

Недели	Пассажиро-мили, тыс.	Недели	Пассажиро-мили, тыс.
1-я	17	7-я	20
2-я	21	8-я	18
3-я	19	9-я	22
4-я	23	10-я	20
5-я	18	11-я	15
6-я	16	12-я	22

а) Считая начальный прогноз для недели 1 в 17000 миль и используя экспоненциальное сглаживание, рассчитайте прогноз для недель со второй до двенадцатой. Примите а = .2.

б) Чему равно MAD для этой модели?

в) Рассчитайте RSFE и трекинговые сигналы. Везде ли они находятся в установленных лимитах?

Ответ 4.23: а) 17.00; 17.80; 18.04; 19.03: 18.83; 18.26; 18.61; 18.49; 19.19; 19.35; 18.48;

б) 2.60;

в) нет, трекинговый сигнал превосходит 5 сигм в неделю 10.

Задача 4.24.ПК

Число поездок на автобусах и в метро в городе увеличивается в течение летних месяцев в зависимости от числа туристов, приезжающих в город. В течение последних 12 лет получены следую­щие данные:

Год	Число туристов, млн. чел.	Поездки, млн.
1-й	7	1.5
2-й	2	1.0
3-й	6	1.3
4-й	4	1.5
5-й	14	2.5
6-й	15	2.7
7-й	16	2.4
8-й	12	2.0
9-й	14	2.7
10-й	20	4.4
11-й	15	3.4
12-й	7	1.7

а) Введите эти данные в ПК и определите возможность ис­пользования линейной регрессионной модели.

б) Постройте регрессионное уравнение.

в) Сколько поездок будет в этом году, если число туристов, посещающих город, составит 10 млн. человек?

г) Сколько поездок будет при отсутствии туристов?

д) Определите стандартную ошибку прогноза.

е) Чему равен коэффициент корреляции модели и коэффици­ент детерминации?

Ответ 4.24: б) у =.5 + 159х;

в) 2.1 млн.;

г) 511000, но х = 0 не должно быть в рассматриваемых значениях;

д) .4;

е) r =.92, r² = .84.

Задача 4.25.ПК

Число вызовов 911 для последних 24 недель показано ниже.

Недели	Вызовы	Недели	Вызовы	Недели	Вызовы
1-я	50	9-я	35	17-я	55
2-я	35	10-я	20	18-я	40
3-я	25	11-я	15	19-я	35
4-я	40	12-я	40	20-я	60
5-я	45	13-я	55	21-я	75
6-я	35	14-я	35	22-я	50
7-я	20	15-я	25	23-я	40
8-я	30	16-я	55	24-я	65

а) Рассчитайте прогноз вызовов для каждой недели методом экспоненциального сглаживания. Примите начальный прогноз 50 вызовов для первой недели и используйте а =.1. Каков будет прогноз для 25-й недели?

б) Перепрогнозируйте каждый период, используя а = .6.

в) Текущие вызовы в течение 25-й недели были равны 86. Какая константа сглаживания дает лучший прогноз? Объясните это расчетом ошибки прогноза.

Ответ 4.25: в) .6 константа сглаживания.

Задача 4.26.ПК

Используя данные из задачи 4.25, спрогнозируйте число вызо­вов для недель со 2-й по 25-ю методом экспоненциального сгла­живания с регулируемым трендом. Примите начальный прогноз 50 вызовов для недели 1-й начальный тренд, равный 0. Исполь­зуйте в качестве констант сглаживания а = .3 и b = .1. Является ли эта модель лучше, чем модель задачи 4.25? Какое регулирование может быть успешным в дальнейшем? (Примите текущие вызовы для 25-й недели равными 85.)

Задача 4.27

Энергетическая компания собирает информацию о спросе на электроэнергию в регионе в течение последних двух лет. Эта информация показана ниже.

Месяц	Спрос, МВт		Месяц	Спрос, МВт
	Прошлый год	Текущий год		Прошлый год	Текущий год
Январь	5	17	Июль	23	44
Февраль	6	14	Август	26	41
Март	10	20	Сентябрь	21	33
Апрель	13	23	Октябрь	15	23
Май	18	30	Ноябрь	12	26
Июнь	15	38	Декабрь	14	17

Стандартные прогнозные модели, обсуждаемые ранее, не под­ходят к данным, представленным для двух лет.

а) В чем слабость стандартных методов прогнозирования при­менительно к этим данным?

б) Поскольку известные модели не применимы здесь, предло­жите ваш подход к прогнозированию.

в) Спрогнозируйте спрос для каждого месяца следующего го­да, используя предложенную вами модель.

Задача 4.28

Посещаемость новейших аттракционов Дисней-ленда была следующая:

Год	Сезон	Посетители, тыс. чел.
1990	Зима	73
	Весна	104
	Лето	168
	Осень	74
1991	Зима	65
	Весна	82
	Лето	124
	Осень	52
1992	Зима	89
	Весна	146
	Лето	205
	Осень	98

Рассчитайте сезонные индексы, используя эти данные.

Ответ 4.28: .709, 1.037, 1.553, .700.

Задача 4.29

Менеджер департамента фирмы использует экстраполяцию временных серий для прогнозирования объема продаж в следую­щих четырех кварталах. Для прошлых кварталов продажи были равны $120000, $140000, $160000, $180000. Сезонные индексы, найденные соответственно для четырех кварталов, составляют 1.25, .90, .75 и 1.15.

Рассчитайте прогноз объема продаж.

Ответ 4.29: у₁ = $150000; у₂ = $126000; у₃ = $120000; у₄ = $207000.

Задача 4.30.ПК

Имея прошлые данные о депозитах и величине валового про­дукта региона за 44 года (валовый продукт региона аналогичен ВНП, но на уровне региона), построить долговременный страте­гический план, включающий пятилетний прогноз депозитов.

а) Используя экспоненциально сглаживание с а =.6, затем трендовый анализ и, наконец, линейную регрессию, обсудите, какая прогнозная модель является лучшей для стратегического плана. Объясните, почему одна модель лучше, чем другие.

б) Посмотрите исходные данные. Можете ли вы исключить из набора какие-либо порции информации? Почему? Как изменится выбор вами модели?

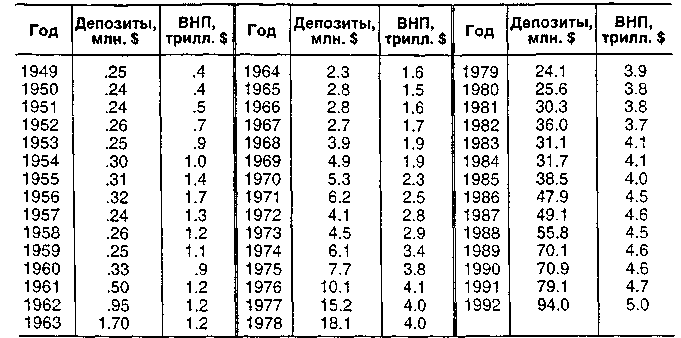
Ответ 4.30: MAD для экспоненциального сглаживания = 3.5;

MAD для тренда = 10.6; MAD для уравнения регрессии = 10.25.