Теория вероятностей — математическая наука, изучающая зако­номерности, присущие массовым случайным явлениям. При этом из­учаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы. То есть теория вероятностей рассматрива­ет не сами реальные явления, а их упрощенные схемы — математиче­ские модели.

Становление теории вероятности как математической науки связано с именем Я. Бернулли(1654-1705), который ввел классическое определение события и доказал простейший случай закона больших чисел.

Цель теории вероятностей — осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, огра­ничение сферы действия случайности.

1. Понятие «случайного события»

Основным и важным понятием, науки теории вероятности является термин «случайного события».

Случайным событием (или просто: событием) называется любой исход опыта, который может произойти или не произойти.

Операции над событиями можно проиллюстрировать с помощью диаграмм Эйлера-Венна на рис.1:

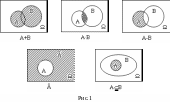
Операции над событиями обладают следующими свойствами:

• А+В=В+А, А∙В=В∙А (переместительное);

• (А+В)∙С=А∙С+В∙С, А∙В+С=(А+С)∙(В+С) (распределительное);

• (А+В)+С=А+(В+С), (А∙В)∙С=А∙(В∙С) (сочетательное);

• А + А = А, А ∙ А = А;

• А + Ω = Ω, А ∙ Ω = А;

- 3 -

• А + = Ω, А ∙ = ;

• = Ω, Ω = , = А;

• А - В = А ∙ ;

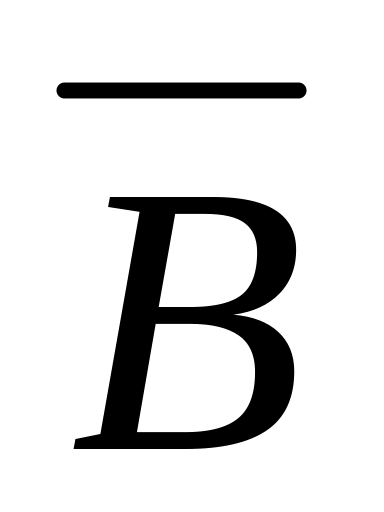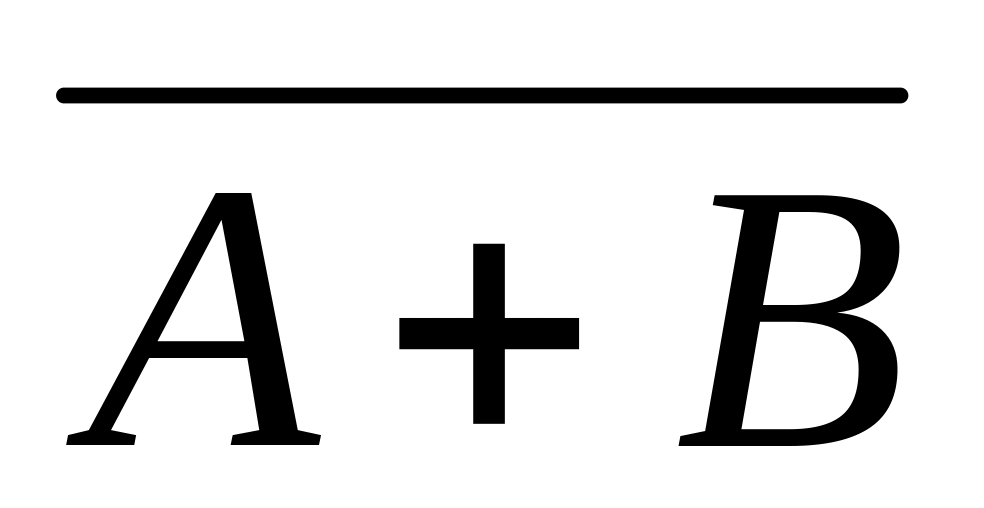• = ∙ и 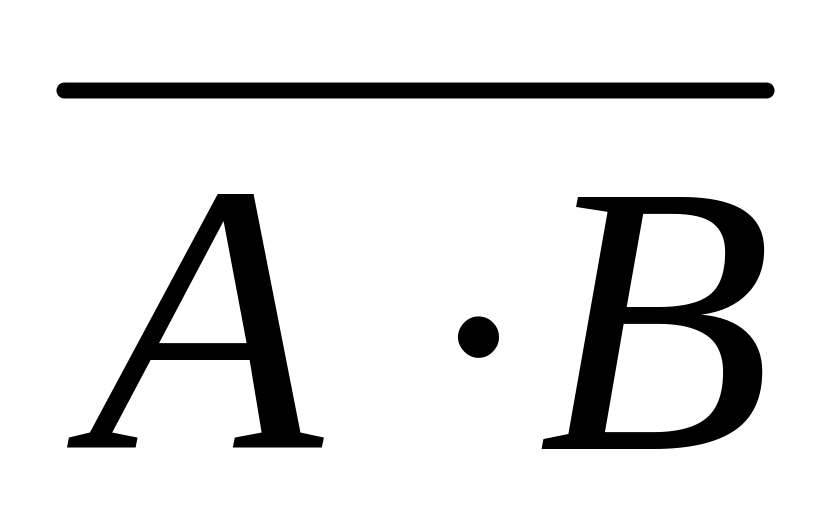= + — законы де Моргана.

Например, рассмотрим опыт: бросание игральной кости; событие А — выпадение 5 очков, событие В — выпадение четного числа очков, событие D — выпадение целого числа очков, событие Е — выпадение не менее 3-х очков. Эти события будут состоять из следующих из элементов В={2, 4, 6}, Е={3, 4, 5, 6}, А={5}, D={1, 2, 3, 4, 5, 6}.

Тогда: В + Е = {2, 3, 4, 5, 6}, B ∙ E = {4, 6}, В - Е={2}. Противоположным событию A будет событие состоящее из следующих элементов = {1, 2, 3, 4, 6}, событию В  D, так как D = {1, 2, 3, 4, 5, 6}, то есть D= Ω.

Пример. Доказать формулу А + В = А + В.

Решение. Используя некоторые из выше приведенных правил, получаем: А+В = (А + В) ∙ Ω = А∙Ω + В∙Ω= A∙Ω + B∙ (A+ ) = А∙Ω + (А+ ) ∙В = A∙Ω + A∙B + ∙B = (Ω + B) ∙A + ∙B = Ω∙A + ∙B = A + ∙В.

Таким образом, сумму любых двух событий можно представить в виде суммы двух несовместных событий.

Геометрическое доказательство представлено на рис. 2.

Задачи для самостоятельного решения.

1. Доказать формулы: а) В = АВ+ В; б) (А+С)(В + С) = АВ+С; в) .

2. Пусть А, В и С — три произвольных события. Выразить через них следующие события: а) произошли все три события; б) произошло только С; в) произошло хотя бы одно из событий; г) ни одного события не произошло; д) произошли А и В, но С не произошло; е) произошло одно из этих событий; ж) произошло не более двух событий.

- 4 -

3 . Релейная схема (рис. 3) состоит из 6 элементов. Пусть события A_i (i = 1,6) состоят в том, что соответствующие элементы работают безотказно в течение времени Т. Выразить через A_i событие, состо­ящее в том, что схема за время Т работает безотказно.

2. Статистическое и классическое определение вероятности

Классической вероятностью события А называется отношение числа т случаев благоприятствующих этому событию, к общему числу n случаев, т. е.

.

Статистической вероятностью события А называется число, около которого колеблется относительная частота события А при до­статочно большом числе испытаний (опытов).

Предполагается, что элементарные исходы образуют полную группу и равновозможны.

Пример 1. В урне (емкости) находятся 12 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?

Решение. Пусть А — событие, состоящее в том, что вынут белый шар. Яс­но, что n = 12 + 8 = 20 — число всех равновозможных случаев (исхо­дов опыта). Число случаев, благоприятствующих событию А, равно 12, т.е. т = 12. Следовательно, по формуле классического определения вероятности имеем: , т.е. Р(А)= 0,6.

Пример 2. Найти вероятность того, что в наудачу написанном двухзначном числе все цифры разные.

Решение. Пусть A – событие, состоящее в том, что написанное двухзначное число, имеет две разные цифры. Из 90 двухзначных чисел (от 10 до 99) 9 из них имеют одинаковые числа – это числа 11, 22, 33, 44, 55, 66, 77, 88, 99.

- 5 -

Тогда общее количество равновозможных случаев n = 90, а количество благоприятствующих для данного события m = 90 – 9 = 81. По формуле классического определения вероятности получаем , т. е. P(A) = 0,9.

Пример 3. В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки: а) одинаковы, б) различны.

Решение. Общее количество равновозможных исходов n, будем вычислять, используя формулу комбинаторики – сочетания с повторением. Выбрать 4 открытки из 6 видов можно =84 способами, т. е. n = 84.

а) Пусть событие A – состоит в том, что продано 4 одинаковые открытки. Число m исходов благоприятствующих наступлению события A, равно числу видов открыток m = 6. Тогда по формуле классического определения вероятности .

б) Пусть событие B – состоит в том, что проданы 4 различные открытки. Выбрать 4 открытки из 6 можно =15 способами, т. е. m=15. Следовательно, по формуле получаем

Пример 4. В коробке 5 синих, 4 красных и 3 зеленных

карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что среди них 2 синих и 1 зеленый карандаш?

Решение. Сначала найдем общее число способов выбора 3 карандашей из 12, имеющихся в наличии. Это и будет число благоприятствующих случаев. Сделаем это с помощью формулы сочетания без повторений .

Пусть событие А – из трех выбранных карандашей, 2 синих и 1 зеленый. Выбрать 2 синих карандаша из имеющихся 5 синих, можно сочетанием 2 из 5, то есть способами, а 1 зеленый из имеющихся 3 зеленых - способами.

- 6 –

Отсюда по правилу умножения получаем = 10∙3=30. Тогда, по формуле классического определения вероятности .

Пример 5. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту, появления бракованных книг.

Решение. Относительная частота события А – появление бракованных книг, равна отношению числа испытаний, в которых появилось событие А, к общему числу произведенных испытаний: n=100 – общее число произведенных событий, =5 – число событий, в которых появилось событие А. Тогда