V. Элементы функционального анализа Тема 8. Метрические пространства. Основные понятия

1. Понятие метрического пространства.

2. Примеры метрических пространств.

3. Окрестности точек в метрическом пространстве. Классификация точек и множеств в метрическом пространстве.

4. Определения и свойства открытых и замкнутых множеств точек метрического пространства.

См. список литературы: [1, гл. 3.1 –3.4]; [4, гл. 7.1 –7.2].

Краткие теоретические сведения

1. Метрическим пространством называется произвольное множество М элементов, называемых точками, в котором для любой пары элементов определено число , называемое расстоянием от х до у (или метрикой), обладающее следующими свойствами:

а) для любых , причем тогда и только тогда, когда х = у (аксиома тождества);

б) для любых (аксиома симметрии);

в) для любых (аксиома треугольника).

2. Примеры метрических пространств.

Евклидовы пространства : множество упорядоченных групп из n элементов действительных чисел , где с расстоянием . В частности, при n=1 возникает пространство (множество действительных чисел R).

Гильбертово пространство . Множество числовых последовательностей , для которых (т.е. ряд сходится). Метрика: .

Пространство непрерывных на функций . Элементы – непрерывные функции на ; .

3. Определение шара в метрическом пространстве. Шаром метрического пространства М с центром в точке и радиусом называется множество точек , удовлетворяющих неравенству .

Задачи

107. Будет ли множество R действительных чисел метрическим пространством, если расстояние между элементами х и у определить формулами:

а) ; б) ?

107. Будет ли множество точек плоскости хОу метрическим пространством, если расстояние между точками и определить формулой ?

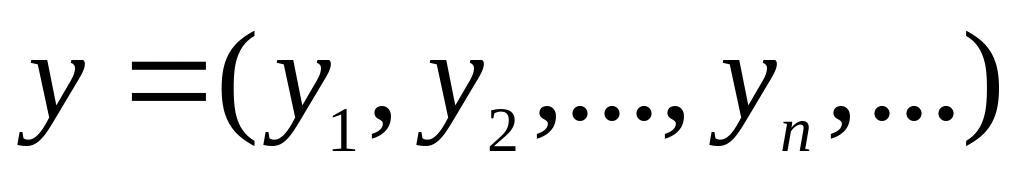108. Доказать, что множество последовательностей , удовлетворяющих условию , образует метрическое пространство, если расстояние между элементами и определить формулой 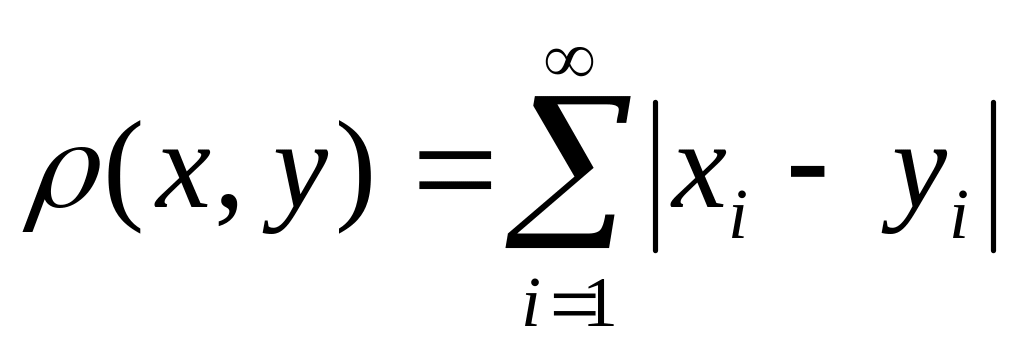. Что представляет собою в этом пространстве шар , где ? Привести примеры элементов, принадлежащих этому шару.

109. Используя неравенства Коши-Буняковского: ; , показать, что и являются метрическими пространствами.

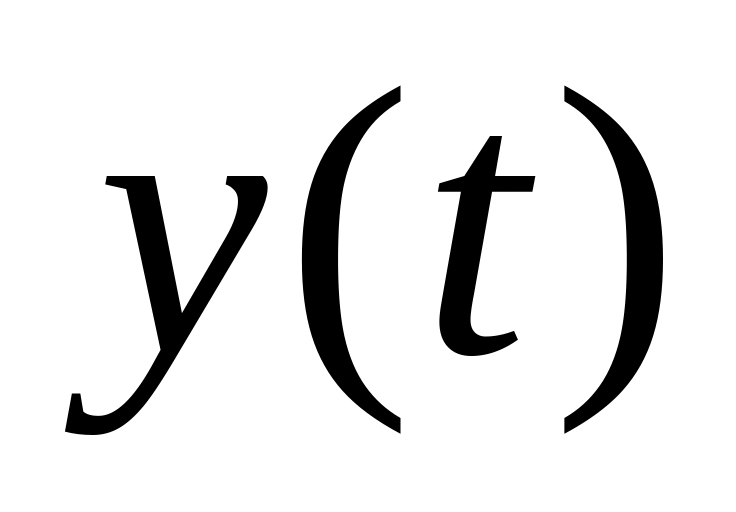110. Доказать, что множество М всех ограниченных (не обязательно непрерывных) на отрезке функций образует метрическое пространство, если расстояние между элементами и определить формулой .

111. Доказать, что множество непрерывных на отрезке функций образует метрическое пространство С₁ , если расстояние между элементами и определить формулой .

112. Доказать неравенства Коши-Буняковского для интегралов: а) ; б) .

113. Доказать, что множество непрерывных на отрезке функций образует метрическое пространство С₂, если расстояние между элементами и определить формулой .

Тема 9. Полнота метрических пространств

1. Полные метрические пространства.

2. Полнота пространств Rⁿ, C_[a,b].

См. список литературы: [1, гл. 3.5]; [4, гл. 7.3 – 7.6].

Краткие теоретические сведения

Последовательность точек метрического пространства называется фундаментальной, если при , т.е. .

Метрическое пространство М называется полным, если в нем каждая фундаментальная последовательность сходится, т.е. если – фундаментальная, то существует , такая, что .

Задачи

107. Пусть – метрика множества Х. Доказать, что функции , , также являются метриками этого множества. Являются ли полными полученные метрические пространства, если в метрике множество Х – полное метрическое пространство?

108. Доказать, что следующие множества с заданными на них метриками являются полными метрическими пространствами:

1) множество числовых последовательностей , удовлетворяющих условию , с метрикой ;

2) множество числовых последовательностей , удовлетворяющих условию , с метрикой ;

3) множество C_[a,b] всех непрерывных на отрезке [a, b] функций с метрикой _;

_{4) множество СВ(a,b) всех ограниченных непрерывных на интервале (a,b) функций с метрикой ;}

_{5) множество В(a,b) всех ограниченных функций на интервале (a,b) с метрикой .}

107. _{Будет ли полным метрическим пространством вещественная прямая с метрикой:}

_{а) ; б) ; в) ?}

107. Показать, что множество рациональных чисел не является полным метрическим пространством, если расстояние между двумя числами определено формулой .

108. Показать, что множество 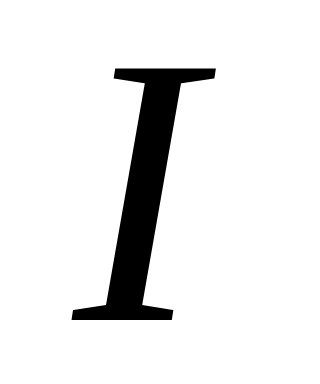иррациональных чисел не является полным метрическим пространством, если расстояние между двумя числами определено формулой .

109. Доказать, что всякое замкнутое множество Е точек полного метрического пространства М является полным метрическим пространством, если расстояние между точками множества Е определяется так же, как и в пространстве М.