Исходные данные для портфеля

Акция	Цена покупки, p0	Поступления на конец года Si с вероятностью qi
		q1 = 0,3	q2 = 0,4	q3 = 0,2	q4 = 0,1
1	200	206	230	224	238
2	150	165	165	150	169,5
3	100	108	112	111	102

Доходность каждой акции зависит от ситуации на фондовом рынке и определяется по формуле:

(5.6)

где S_ί = p_ί + d_ί; p_ί – курсовая стоимость на конец года; d_ί – размер дивидендов; - стоимость на начало года.

Отсюда можно определить ожидаемую доходность , дисперсию и среднее квадратическое отклонение :

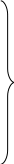
(5.7)

Результаты расчета статистических характеристик доходности для рассматриваемой задачи даны в табл.5.2.

Таблица 5.2

Статистические характеристики активов портфеля, %

№	Вероятности рыночной ситуации
	q1=0,3	q2=0,4	q3=0,2	q4=0,1
1	3	15	12	19	11,2	32,16	5,6710
2	10	10	0	13	8,3	18,01	4,2438
3	8	12	11	2	9,6	9,24	3,0397

Данные, приведенные в таблице, можно интерпретировать следующим образом: если ситуация на рынке соответствует состоянию, имеющему вероятность реализации, например, q = 0,4, то инвестор будет иметь доходность 15%, 10% и 12% по каждому виду ценных бумаг соответственно. На основе вероятных доходностей по формулам (5.16) получены ожидаемые доходности и показатели вариации.

В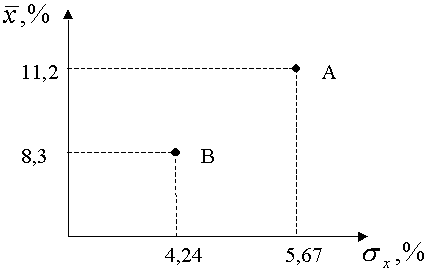 начале рассмотрим портфель, состоящий всего из двух видов акций (1 и 2). Тогда в прямоугольной системе с координатами «доходность-риск» можно получить две характерные точки А и В (рис.5.3).

Рис.5.3. Графическая интерпретация ситуации при отказе от формирования портфеля

Точка А отражает ситуацию, когда все 60 тыс.руб. вложены в акции вида 1, а точка В соответствует варианту вложения всех денежных средств в акции второго типа.

Возникает естественный вопрос, к каким последствиям приведет принятие решения о формировании портфеля из этих двух активов с долями α₁ и α₂, причем .

Например, инвестор тратит 20% свободных средств (12 тыс. руб.) на покупку акций первого вида и 80% (48 тыс. руб.) – на акции второго вида, то есть портфель включает 60 акций вида 1 и 320 акций вида 2.

Тогда на основе данных табл.5.2 можно получить вероятностные характеристики портфеля в целом (табл.5.3).

Средневзвешенная доходность такого портфеля:

= 0,3 8,6+0,4 11+0,2 14,2+0,1 2,4=8,88%

Таблица 5.3

Вероятностные характеристики портфеля из двух ценных бумаг

№	Число акций	Цена пакета, тыс.руб.	Поступления на конец года с вероятностью тыс.руб.
			q1=0,3	q2=0,4	q3=0,2	q4=0,1
1	60	12	12,36	13,8	13,44	14,28
2	320	48	52,80	52,8	48,00	54,24
Σ	380	60	65,16	66,6	61,44	68,52
	-	-	8,6	11,0	14,2	2,4

Дисперсия:

= 0,3(8,6-8,88)² + 0,4(11-8,8)² + 0,2(14-8,88)² + 0,1(2,4-8,88)² = =13,05.

Среднее квадратическое отклонение:

= 3,61

Е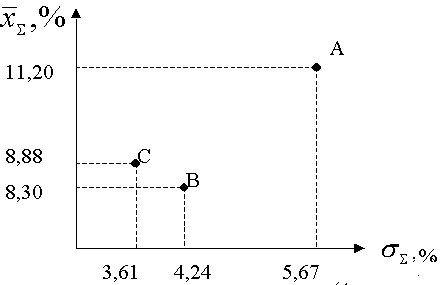 сли отобразить на предыдущем графике координаты полученного портфеля (рис.5.4), то изображающая точка С показывает важнейшее свойство портфеля: его риск меньше, чем риск составляющего актива с самым низким риском.

Рис.5.4 Доходность и риск для отдельных активов (А и В) и для портфеля

Полученный результат приводит к необходимости поиска закономерностей изменения доходности и риска портфеля в зависимости от его структуры. Из табл. 5.3 следует, что независимо от ситуации ожидаемая доходность портфеля определяется по формуле средней арифметической взвешенной из доходности составляющих активов:

.

Для оценки риска портфеля необходимо знать дисперсии доходности содержащихся в нем ценных бумаг, долю каждой из них в портфеле, а также показатели, характеризующие статистическую зависимость между случайными значениями доходностей бумаг. Дело в том, что портфель представляет собой систему случайных величин, а для изучения системы недостаточно знания индивидуальных статистических характеристик, то есть математического ожидания и дисперсии. Эти характеристики не отражают связь величин между собой. Для оценки статистической зависимости используют корреляционный момент (ковариацию) и коэффициент корреляции между которыми существует функциональная связь:

(5.8)

Для дискретных случайных величин корреляционный момент определяется суммой:

, (5.9)

где n – число возможных состояний (ситуаций); - средние значения случайных величин.

Однако корреляционный момент характеризует не только зависимость случайных величин, но и их рассеивание. Величина при одной и той же степени связи величин х и y будет различной в зависимости от того, какими будут отклонения этих величин от средних значений – большими или малыми. Для характеристики связи в чистом виде используют коэффициент корреляции ρ_xy. Случайные величины х и y называют коррелированными, если К_xy ≠ 0 (ρ_xy≠0) и некоррелированными, если К_xy = 0 (ρ_xy=0).

При ρ_xy>0 существует положительная, а при ρ_xy<0 – отрицательная корреляция. При положительной корреляции между активами с возрастанием доходности одного из них, доходность другого имеет тенденцию в среднем возрастать. При отрицательной корреляции наблюдается другая закономерность: с возрастанием доходности акции 1 доходность акции 2 в среднем имеет тенденцию убывать. Если величины х и y связаны детерминированной, то есть точной функциональной линейной зависимостью:

y = a+bx,

то коэффициент корреляции ρ_xy = ±1 (знак плюс при b>0, знак минус при b<0).

Таким образом, числовыми характеристиками системы нескольких случайных величин, то есть набора рисковых финансовых инструментов, являются средние доходности составляющих активов и корреляционная матрица:

(5.10)

Корреляционная матрица является симметричной относительно главной диагонали, так как справедливо равенство:

К_ίj=К_{jί ,} (ij=1,2…n).

Элементы главной диагонали представляют собой дисперсии доходностей отдельных акций.

К_ίί=σ_ί (i=1,2…n).

Дисперсия суммы нескольких случайных величин, то есть риск портфеля равен средневзвешенной сумме элементов корреляционной матрицы, а для случая двух активов:

=

= , (5.11)

где К₁₂ - корреляционный момент (ковариация) между активами 1 и 2; - соответствующий коэффициент корреляции.

Ковариация между активами определяется по формуле (5.9):

К₁₂= 0,3(3-11,2) (10-8,3)+0,4(15-11,2) (10-8,3)+

+0,2(12-11,2) (0-8,3)+0,1(19-11,2) (13-8,3)= 0,74

Коэффициент корреляции:

Полученное значение показывает пренебрежимо малую статистическую связь между активами.

Поэтому, если воспользоваться формулой (5.11), то получим для риска портфеля тот же результат, который получен ранее:

Используя полученные соотношения, можно за счет изменения структуры портфеля получить все возможные комбинации в координатах «доходность-риск» (табл.5.4.)

Таблица 5.4.