106

5. Принципы выбора рискованных решений

Риск представляет собой событие, которое может произойти с предполагаемой (априорной) вероятностью. Вероятность определяется мерой возможности свершения данного события и изменяется в пределах от нуля для невозможного события до единицы – для достоверного события. Количественная оценка риска в экономике выполняется на основе прошлого опыта и интуиции с использованием текущей и ретроспективной информации.

В связи с неполнотой и неточностью исходной информации оценка риска практически всегда имеет приближенный характер. Кроме того, на практике часто возникают ситуации, когда даже вероятностные оценки относительно будущих событий получить в принципе невозможно. Такие ситуации в общепринятой терминологии классифицируют как принятие решений в условиях неопределенности.

В условиях риска применяют один из следующих критериев: среднего ожидаемого значения, ожидаемого значения с учетом его возможной вариации; критерий предельного уровня и критерий наиболее вероятного (модального) исхода. На практике чаще всего используют первые два критерия, которые представляют собой естественный переход от условий полной определенности.

Критерий ожидаемого значения. Применение этого критерия можно показать на примере денежных потоков. Точные цифры поступлений и выплат по годам никогда неизвестны, то есть и поступления, и выплаты представляют собой случайный процессы, для которых мы можем предсказать лишь средние значения (математическое ожидание) и возможный разброс относительно этих средних (вариацию). Поэтому критерии максимума средней прибыли, средней доходности и средних издержек соответствуют критерию среднего ожидаемого значения.

Иногда считаются известными вероятности реализации определенных событий. Например, вкладывая в дело 100 тыс. руб., мы уже заранее знаем, что эти инвестиции могут через два года дать доход 600 тыс. руб. с вероятностью 0,7 или 200 тыс. руб. с вероятностью 0,3. Тогда по критерию ожидаемого значения мы должны получить чистый доход:

600 0,7 + 200 0,3 - 100 = 420 + 60 - 100 = 380 тыс. руб.

Критерий «ожидаемое значение – вариация». Любые средние – это условные величины, которые используют для свертки множества случайных значений показателя в одно число. Поэтому фактические значения могут существенно отличаться от средних величин. Другими словами, разброс исходной информации приводит к необходимости учета рисковой надбавки.

Если речь идет о доходах, то эта надбавка, естественно, должна вычитаться из среднего значения и используется нижняя граница.

В прогнозах издержек, убытков, потерь, наоборот, эта надбавка добавляется, то есть используется верхняя граница.

В математической формулировке соответствующие критерии записываются в виде:

; (5.1)

(5.2)

где σ_п , σ_z – средние квадратические отклонения для прибыли и издержек соответственно; t - коэффициент кратности, который определяют либо по таблицам нормального распределения (большая выборка), либо по таблицам Стьюдента (малая выборка) в зависимости от требуемого уровня доверия к результатам расчета;

_п , _z - рисковые надбавки.

На этапе предварительного анализа и для ориентировочных расчетов, если нет более точной информации, рисковую надбавку можно рассчитать двумя способами. В первом случае, на основе оценки точности исходной информации задают возможные пределы изменения прибыли или издержек в процентах к среднему значению, например, годовая прибыль П = 50 тыс.руб. + 20%. Тогда ожидаемое значение прибыли с учетом риска будет 40 тыс.руб. и никакие вычисления не требуются. Другой способ заключается в том, что исполнитель задает три возможные оценки показателя: минимальную (x ), наиболее вероятную (x ), максимальную (x ). Тогда в предположении бета-распределения соответствующего показателя рассчитывают среднее значение и среднее квадратическое отклонение :

^(5.3)

^(5.4)

При этом наиболее вероятные оценки могут быть смещены вправо или влево при левосторонней или правосторонней асимметрии распределения (рис.5.1) соответственно:

Цифра шесть в знаменателе соответствует правилу трехсигмальной зоны, то есть возможные отклонения от среднего значения почти со стопроцентной вероятностью (99,7%) укладываются в промежуток + 3σ_x . Это свойство можно использовать в имитационном моделировании при формировании исходной информации, где необходимо знать вероятностные характеристики и σ_x.

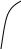
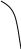
Рис. 5.1. Возможные виды бета - распределения показателя

Тогда для расчета достаточно лишь получить оценку среднего значения и возможные пределы его изменения. Например, если интервал изменения прибыли 50 20 тыс.руб. равен 40 тыс.руб., то среднее квадратическое отклонение составляет 40/6 = 6,7 тыс.руб., а коэффициент вариации V = 6,7/50 = 0,134 = 13,4%.

Мы рассмотрели теоретический способ расчета рисковой надбавки. На практике коэффициент кратности t определяет сам предприниматель в зависимости от его склонности или несклонности к риску. Поэтому осторожный предприниматель может выбрать t намного больше 1, что уменьшает вероятность потерь, а склонный рисковать - доли единицы.

Критерий предельного уровня не позволяет получить оптимальное решение в виде максимума прибыли или минимума затрат. Однако он определяет приемлемый способ действий. Например, владелец недвижимости продает свою квартиру. Узнав предложенную цену, продавец должен в предельно короткий срок решить, приемлема ли она для него. С этой целью он заранее устанавливает предел цены, ниже которой квартира не может быть продана. Это и есть предельный уровень, который позволяет продавцу согласиться на первое же предложение, превышающее этот уровень.

Данный критерий не приводит к оптимальному решению, так как среди следующих предложений может быть более выгодное, чем принятое.

В этом критерии не используются вероятности возможного исхода, но все равно он является критерием риска. Дело в том, что устанавливая цену, продавец знает примерное распределение цен на жилье. В противном случае он установил бы слишком высокую или слишком низкую цену. В первом случае квартира не может быть продана, так как любая предложенная цена будет отвергнута, а во втором – продавец не получит достаточной компенсации за жилье.

Критерий наиболее вероятного исхода основан на замене случайной величины прибыли или издержек ее модальным значением с наибольшей вероятностью реализации. При этом случайная ситуация преобразуется в неслучайную (детерминированную), а вместо среднего используется мода. Например, возможный доход от продажи товара характеризуется дискретным рядом распределения:

Доход, млн. руб.	4	6	8	10	12
Вероятность получения дохода pi	0.1	0.2	0.4	0.2	0.1

В качестве критерия принимают модальное значение предполагаемого дохода, равное 8 млн. руб.

В отличие от ситуаций с риском в условиях неопределенности никакие вероятностные характеристики не известны. При этом в качестве количественных критериев принятия решений используют один из следующих критериев: критерий Лапласа, минимаксный критерий, критерий Сэвиджа, критерий Гурвица.

Не существует общих правил для оценки области применения каждого из них, так как отношение лица, принимающего решение, в конкретной ситуации является определяющим при выборе того или иного критерия.

Данные, необходимые для принятия решений в условиях неопределенности, обычно представляют в виде матрицы, строки которой соответствуют возможным действиям, а столбцы – возможным состояниям системы. Каждый элемент матрицы, находящийся на пересечении строк и столбцов, соответствует результату, определяющему доход или потери при выборе данного действия и реализации данного состояния.

Таким образом, если d_i представляет действие с номером i ( i = 1, 2, … m ) и S_j представляет возможное состояние с номером j ( j = 1, 2, … n ), то R_ij соответствует результату R(d_i, S_j) при выборе данного действия и реализации данного состояния.

	S1	S2	...	S
d1	R	R12	...	R
d2	R21	R22	...	R
…	...	…	…	…
d	R	R	…	R

Например, несколько предпринимателей на основе изучения конъюнктуры рынка решили на долевых началах построить специализированное авторемонтное предприятие. На основе изучения статистической информации в предполагаемой зоне обслуживания установлено, что число заказов на ремонт из года в год может изменяться в пределах от 200 до 350 единиц. Проектная организация предлагает на выбор несколько типовых проектов, рассчитанные на ремонт 200, 250, 300 и 350 автомобилей в год. Задача заключается в выборе варианта проекта.

Дело в том, что отклонения фактической загрузки мощностей от проектных вариантов приводят к дополнительным потерям либо из-за превышения предложения над спросом (неполная загрузка), либо из-за неполного удовлетворения спроса (перегруза). Возможные затраты и потери в млн. руб. сведены в матрицу:

	200	250	300	350
200	5	10	18	25
250	8	7	8	23
300	21	18	12	21
350	30	22	19	15

Критерий Лапласа. Поскольку из-за полного отсутствия информации вероятности состояний S₁, S₂, … S_n неизвестны, то нельзя утверждать, что эти вероятности различны. В противном случае можно определить эти вероятности и уже нет необходимости рассматривать ситуацию как принятие решений в условиях неопределенности.

Поэтому согласно принципу недостаточного обоснования состояния рынка S₁, S₂, … S_n имеют равные вероятности. Тогда исходную задачу можно рассматривать как задачу принятия решений в условиях риска, когда выбирается действие, дающее наибольший ожидаемый выигрыш в соответствии с условиями

 , если R_ij – доход

(5.5)

 , если R_ij – потери

где n – число состояний, 1/n – вероятность реализации любого из состояний (поскольку они равны между собой).

Тогда в соответствии с условием (5.5) ожидаемые потери при реализации разных проектов составляют:

З (d₁) = 0,25 (5+10+18+25) = 14,5

З (d₂) = 0,25 (8+7+8+23) = 11,5;

З (d₃) = 0,25 (21+18+12+21) = 18,0;

З ( ) = 0,25 (30+22+19+15) = 21,5;

Критерий минимакса (максимина). Данный критерий является наиболее осторожным, так как основан на выборе наилучшей из наихудших возможностей. Если результат R_ij, представляет собой потери, то для действия d_i наибольшие потери независимо от возможного состояния S будут равны . Если исходная матрица представляет собой матрицу потерь, используют критерий минимакса, а если дохода – максимина. В нашем примере исходная информация – матрица потерь.

	S1	S2	S3	S4
d1	5	10	18	25	25
d2	8	7	8	23	23
d3	21	18	12	21	21
d4	30	22	19	15	30

Отсюда следует, что минимаксной стратегией будет не d₂, как по критерию Лапласа, а d₃. То есть оптимальным решением является выбор проекта с программой 300 ремонтов в год.

Критерий Сэвиджа. Критерий минимакса основан на таких пессимистических предпосылках, что иногда приводит к нелогичным выводам. Например, рассмотрим следующую матрицу потерь в млн. руб.

d1	11	0,1	11
d2	10	10	10

Согласно минимаксному критерию следует выбрать вариант d₂. Но даже по интуиции большинство людей выберет d₁ , так как вполне возможно, что S₁ будет равно S₂ и потери составят всего 100 тыс. руб. Выбор второго варианта всегда приводит к потере 10 млн. руб. Поэтому критерий Сэвиджа предусматривает введение новой матрицы потерь, где Rij заменяются на r_ij, которые определяют следующим образом:

m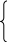 ax R_kj  - R_ij, если R_ij - доход

r_ij =

R_ij – min R_ki, если R_ij – потери