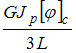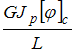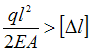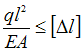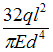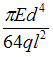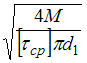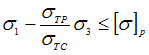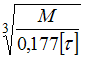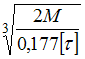Решение:

  ЗАДАНИЕ N 19 отправить сообщение разрабо Тема: Статические моменты. Центр тяжести плоской фигуры Статические моменты фигуры относительно осей x и y равны:   

			2,36; 0
			3,14; 0
			2,36; 2,36
			3,93; –2,36

Решение: Ось y проходит через центр тяжести фигуры. Следовательно 

  ЗАДАНИЕ N 20 отправить сообщение разраб Тема: Главные оси и главные моменты инерциим Главные центральные моменты инерции фигуры, состоящей из двух швеллеров №10, равны: 

			348; 258,5
			232; 155
			482; 368,7
			183,3; 128

Решение: Из таблицы ГОСТов берем характеристики швеллера №10:  Фигура имеет две оси симметрии x, y. На пересечении этих осей расположен центр тяжести фигуры, а оси симметрии являются главными центральными осями. Разделим фигуру на два швеллера. Оси x₁, x₂, y₁, y₂ являются главными центральными осями швеллеров. Тогда можно записать Подставляя числовые значения, получаем

  ЗАДАНИЕ N 21 отправить сообще Тема: Расчет на прочность при кручении На рисунке показан стержень, работающий на кручение. Если направление момента   изменить на противоположное, то прочность стержня из расчета по максимальным касательным напряжениям …

			не изменится
			уменьшится в 2 раза
			увеличится в 2 раза
			уменьшится в 1,5 раза

Решение: 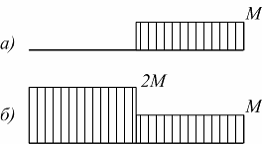На рисунках а и б показаны эпюры крутящих моментов для двух вариантов нагружения стержня. В обоих случаях   Следовательно, при изменении направления момента   на противоположное прочность вала не изменится.

 ЗАДАНИЕ N 22 отправить соо Тема: Расчет на жесткость при кручении 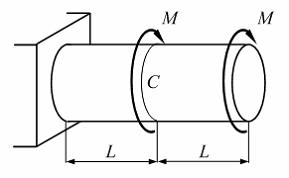На рисунке показан стержень, работающий на кручение. Величины   (допускаемый угол поворота сечения С) заданы. Максимально допустимое значение момента М равно …

  ЗАДАНИЕ N 23 отправить сооб Тема: Крутящий момент. Деформации и напряжения В самых напряженных точках поперечного сечения вала касательные напряжения достигнут предела текучести тогда, когда значение момента Мравно …

Решение: Максимальные касательные напряжения возникают на правом участке. Значение М, при котором эти напряжения станут равными пределу текучести, определим из условия  откуда 

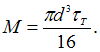
 ЗАДАНИЕ N 24 отпра Тема: Чистый сдвиг. Расчет на сдвиг (срез) Напряженное состояние «чистый сдвиг» показано на  рисунке. Штриховыми линиями показан характер деформации. Углом сдвига называется угол …

 ЗАДАНИЕ N 25 отправить с Тема: Основные понятия, определения, допущения и принципы Основным объектом, изучаемым в сопротивлении материалов, является …

			стержень
			пластина
			оболочка
			массивное тело

 ЗАДАНИЕ N 26 отправить Тема: Модели прочностной надежности В курсе «Сопротивление материалов» все материалы, независимо от особенностей их микроструктуры, принято рассматривать как …

			сплошную среду
			атомную кристаллическую решетку
			совокупность хаотически расположенных кристаллов
			атомную кристаллическую решетку и совокупность хаотически расположенных кристаллов

  ЗАДАНИЕ N 27 отправить соо Тема: Перемещение и деформация Размерность линейной деформации – …

Решение: L – первоначальная длина стержня  – длина стержня после приложения к нему растягивающих сил.  – абсолютное изменение первоначальной длины.  – линейная деформация (величина относительная и безразмерная).

  ЗАДАНИЕ N 28 отправить Тема: Внутренние силы и напряжения Числовой мерой распределения внутренних сил по сечению является …

			напряжение
			продольная сила
			потенциальная энергия
			изгибающий момент

Решение: Числовой мерой распределения внутренних сил по сечению является напряжение. Размерность напряжения   В системе СИ напряжение измеряется в Па, кПа, МПа.

  ЗАДАНИЕ N 29 отправить Тема: Механические свойства и механические характеристики материалов На рисунке показана диаграмма растяжения образца диаметром 0,01 м. Масштаб нагрузки – 1 деление – 0,007 МН.  Предел прочности материала равен ___ МПа.

			446
			112
			357
			268

Решение: Предел прочности − это напряжение, соответствующее максимальной нагрузке, которую может выдержать образец. Предел прочности определяется по формуле   где А – первоначальная площадь поперечного сечения образца. В данном случае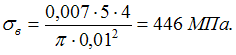 

  ЗАДАНИЕ N 30 отправить сообщ Тема: Продольная сила. Напряжения и деформации Значение продольной силы в сечении С-С равно …

Решение: Сечением С-С делим стержень на две части. Для того чтобы определить продольную силу в сечении, следует рассмотреть равновесие одной из частей. Рассмотрим, например, равновесие левой части (см. рисунок). Продольную силу N направляем от сечения, полагая, что она растягивает материал участка. Уравнение равновесия имеет вид   откуда 

 ЗАДАНИЕ N 31 отправить соо Тема: Расчеты стержней на прочность и жесткость 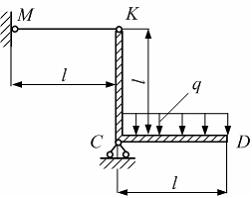Элемент КСD закреплен с помощью шарнирно неподвижной опоры и стержня с жесткостью поперечного сечения на растяжение ЕА (см. рисунок). Система нагружена равномерно распределенной нагрузкой с интенсивностью q. Допустимая величина удлинения стержня   задана. Условие жесткости имеет вид …

 ЗАДАНИЕ N 32 отправить с Тема: Испытание конструкционных материалов на растяжение и сжатие      Вид образца после испытания показан на рисунке. Испытание проводилось по варианту …

			а
			г
			б
			в

(6)

 ЗАДАНИЕ N 1 отправи Тема: Напряжения в поперечном сечении стержня при плоском изгибе    Консольная балка длиной l имеет два варианта расположения прямоугольного поперечного сечения. Сила F, линейные размеры b и h заданы. В опасном сечении балки отношение наибольших нормальных напряжений   равно …

			2
			1
			6
			4

 ЗАДАНИЕ N 2 отправ Тема: Расчет балок на прочность 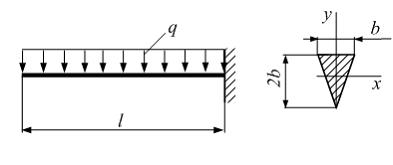Консольная балка длиной   нагружена равномерно распределенной нагрузкой интенсивности   Поперечное сечение – равнобедренный треугольник. Допускаемое нормальное напряжение для материала балки   Из расчета на прочность по нормальным напряжениям размер поперечного сечения балки b равен ____ (см).

			3
			5
			4
			6

 ЗАДАНИЕ N 3 отправи Тема: Поперечная сила, изгибающий момент и их эпюры 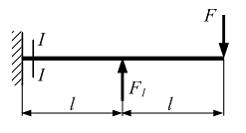Консольная балка длиной   нагружена силами   и   Сечение I–I расположено бесконечно близко в заделке. Изгибающий момент в сечении I–I равен нулю, если значение силы   равно …

  ЗАДАНИЕ N 4 отправить Тема: Перемещения при изгибе. Расчет балок на жесткость 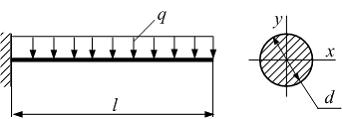Консольная балка длиной l нагружена равномерно распределенной нагрузкой интенсивностью q. Модуль упругости материала Е. Сечение круглое диаметром d. Радиус кривизны оси балки   в опасном сечении равен …

Решение: Кривизна оси стержня в сечении связана с изгибающим моментом, действующим в этом сечении, и жесткостью поперечного сечения на изгиб, в этом же сечении, зависимостью  Опасное сечение расположено вблизи заделки и   Для круглого сечения   После преобразований получим 

  ЗАДАНИЕ N 5 отправить с Тема: Влияние условий закрепления концов стержня на величину критической силы Шарнирно-опертый по концам стержень длиной l сжимается силой F. При постановке в середине пролета промежуточной опоры значение гибкости …

			уменьшится в 2 раза
			не изменится
			увеличится в 2 раза
			уменьшится в 4 раза

Решение: Гибкость стержня определяется по формуле При прочих равных условиях значение гибкости зависит от коэффициента приведения длины   До постановки промежуточной опоры   после постановки  Значение гибкости уменьшится в 2 раза.

 ЗАДАНИЕ N 6 отправить Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня При потере устойчивости сжатого стержня изгиб стержня происходит в плоскости …

			наименьшей жесткости
			наибольшей жесткости
			равнонаклоненной к осям симметрии
			расположенной в любом направлении

  ЗАДАНИЕ N 7 отправит Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Формула Эйлера для определения критической силы применима, если напряжения в сжатом стержне не превышают …

			предела пропорциональности
			предела упругости
			предельного напряжения
			предела текучести

Решение: При выводе формулы Эйлера использовалось приближенное дифференциальное уравнение изогнутой оси стержня. Дифференциальное уравнение, в свою очередь, было получено на допущении, что нормальное напряжение прямо пропорционально линейной деформации  . Закон Гука выполняется до предела пропорциональности. Поэтому формула Эйлера для определения критической силы применима, если напряжения в сжатом стержне не превышают предела пропорциональности.

  ЗАДАНИЕ N 8 отправ Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость Стержень длиной   прямоугольного сечения с размерами   сжимается силой F. Материал стержня – сталь 3  ). Схема закрепления показана на рисунке. Значение критической силы для сжатого стержня равно ______ кН.

			246
			284
			312
			214

Решение: В зависимости от гибкости сжатого стержня критическая сила находится по разным формулам. Определим гибкость стержня  Для прямоугольного сечения минимальный радиус инерции найдем по формуле   где  Тогда  Коэффициент  , который учитывает условия опирания стержня, равен двум. После вычислений находим   Формулу Эйлера, для определения критической силы сжатого стержня при заданной марке материала, использовать нельзя   В случае, когда гибкость стержня, для марки стали 3 лежит в пределах   при определении критического напряжения используют формулу Ясинского  Следовательно, значение критической силы 

  ЗАДАНИЕ N 9 отправить с Тема: Расчет простейших статически неопределимых систем На рисунке показан стержень нагруженный силами F и моментами М. Размер l, диаметр d, модули упругости Е и G заданы. Крутящий момент и продольная сила в сечении С-С, соответственно, равны …

			0, 0

Решение: Стержень геометрически симметричен относительно плоскости симметрии С-С. Нагрузим стержень поочередно моментами М и силами F (рис. 1, 2). В первом варианте (рис. 1) стержень нагружен симметричной нагрузкой. Следовательно в сечении С-С кососимметричный внутренний силовой фактор, крутящий момент, равен нулю. Во втором варианте (рис. 2) стержень  нагружен кососимметричной нагрузкой. Следовательно, в сечении С-С симметричный внутренний силовой фактор, продольная сила, равен нулю. Таким образом, в сечении С-С и во всех сечениях среднего грузового участка крутящий момент и продольная сила равны нулю.

  ЗАДАНИЕ N 10 отправить соо Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина Для данной расчетной схемы формула интеграла Мора имеет вид …

Решение: В данной расчетной схеме стержни работают на растяжение или сжатие. Единственным отличным от нуля внутренним силовым фактором является продольная сила. Следовательно. формула интеграла Мора для данной расчетной схемы имеет вид

  ЗАДАНИЕ N 11 отправи Тема: Статическая неопределимость. Степень статической неопределенности Связи, обеспечивающие кинематическую неизменяемость системы, называются …

			необходимыми
			дополнительными (линейными)
			абсолютно жесткими
			упругими

Решение: 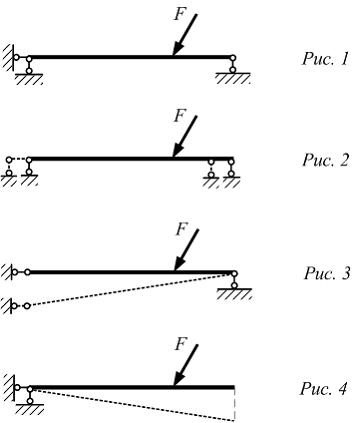На балку наложены три линейные связи (рис. 1). При отбрасывании одной из них балка становится кинематически изменяемой. (рис. 2, 3, 4). Следовательно, все связи являются необходимыми.

  ЗАДАНИЕ N 12 отправить Тема: Метод сил Результат умножения симметричной эпюры на кососимметричную – …

			ноль
			положительное число
			отрицательное число
			число положительное и отрицательно

Решение: 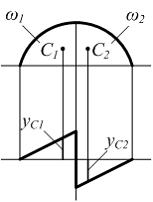На рисунке показаны симметричная и кососимметричная эпюры. Буквами   и   обозначены центры тяжестей площадей   и   Перемножим площади   на ординаты   и сложим произведения. Получим нулевой результат.

 ЗАДАНИЕ N 13 отправи Тема: Расчет на жесткость при кручении На рисунке показаны два стержня из одного материала, работающие на кручение. Поперечное сечения стержня I – круг. Стержень II пустотелый с поперечным сечением в форме кольца. Отношение жесткости поперечного сечения стержня I к жесткости поперечного сечения стержня  II равно …

			1,67
			2,42
			2,78
			0,6

  ЗАДАНИЕ N 14  Тема: Крутящий момент. Деформации и напряжения На рисунке показан стержень, работающий на кручение. Крутящий момент на среднем грузовом участке равен …

			-

Решение: Крутящий момент на среднем грузовом участке определим методом сечений. Разделим стержень на две части произвольным поперечным сечением на среднем участке и рассмотрим равновесие одной из частей (например, левой см. рисунок). Крутящий момент М_кр  направляем произвольно. Уравнение равновесия имеет вид    откуда 

 ЗАДАНИЕ N 15 от Тема: Расчет на прочность при кручении Стержень работает на кручение. Величины М и d заданы. Из условия равнопрочности по напряжениям диаметр вала на правом грузовом участке равен …

 ЗАДАНИЕ N 16  Тема: Чистый сдвиг. Расчет на сдвиг (срез) Два вала диаметрами   соединены между собой с помощью муфты, состоящей из втулки и двух штифтов диаметрами    Соединение передает крутящий момент, равный М. При некотором значении М возможен срез штифтов по сечениям, которые обозначены волнистыми линиями. Значения М,   известны. Минимально допустимый диаметр штифта   из условия прочности на срез равен …

 ЗАДАНИЕ N 17 Тема: Продольная сила. Напряжения и деформации Колонна высотой H (см. рисунок) находится под действием собственного веса и силы F. Удельный вес материала колонны   (вес единицы объема), площадь поперечного сечения А – известны. Максимальные нормальные напряжения в поперечном сечении колонны равны …

  ЗАДАНИЕ N 18  Тема: Механические свойства и механические характеристики материалов Формула, которая связывает упругие постоянные изотропного материала, имеет вид …

Решение: Формула, которая связывает упругие постоянные изотропного материала, имеет вид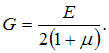 

  ЗАДАНИЕ N 19  Тема: Расчеты стержней на прочность и жесткость Элемент КСD закреплен с помощью шарнирно неподвижной опоры и стержня с жесткостью поперечного сечения на растяжение ЕА (см. рисунок). Система нагружена равномерно распределенной нагрузкой с интенсивностью q. Допустимая величина удлинения стержня   задана. Условие жесткости имеет вид …

Решение: Рассмотрим равновесие элемента КСD и определим продольную силу в стержне   Удлинение стержня   а условие жесткости имеет вид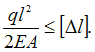 

 ЗАДАНИЕ N 20 о Тема: Испытание конструкционных материалов на растяжение и сжатие  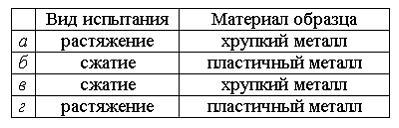      Вид образца после испытаний показан на рисунке. По форме образца и характеру разрушения можно сказать, что испытание проводилось по варианту …

			в
			а
			г
			б

  ЗАДАНИЕ N 21 отправ Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) На рисунке показана тонкостенная трубка, работающая на кручение. Главное напряжение   в точке А действует в направлении …

Решение: Выделим в окрестности точки А элемент стенки трубки двумя поперечными и двумя осевыми сечениями (рис. 1) и повернем его вокруг нормали   на угол, равный   (рис. 2). В этом случае касательные напряжения на гранях элемента будут равны нулю, а главные напряжения       Таким образом, главное напряжение   действует в направлении 

  ЗАДАНИЕ N 22 отправить с Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями На рисунке показано напряженное состояние в точке. Модуль упругости   коэффициент Пуассона   Относительное изменение объема равно …

Решение: Относительное изменение объема определим по формуле   где  Подставляя в формулу числовые значения, получаем 

  ЗАДАНИЕ N 23 отправить с Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности Согласно теории наибольших касательных напряжений (третья теория прочности), самое опасное напряженное состояние показано на рисунке …

			б
			в
			а
			все три напряженные состояния равноопасны

Решение: Согласно теории наибольших касательных напряжений, эквивалентное напряжение определяется по формуле  Определим эквивалентное напряжение для трех вариантов:  а)  , б) , в) . Сравнивая эквивалентные напряжения, можно сказать, что самое опасное напряженное состояние показано на рисунке б.

  ЗАДАНИЕ N 24 отправи Тема: Виды напряженного состояния На рисунке показан стержень, работающий на кручение с растяжением. Напряженное состояние в точке К является – …

			линейное
			плоское
			объемное
			плоское (чистый сдвиг)

Решение: В точке К поперечного сечения действует нормальное напряжение от силы F. Эпюра касательных напряжений от крутящего момента показана на рисунке 1. В угловых точках   Поэтому напряженное состояние в точке К − линейное (одноосное растяжение, рис. 2).

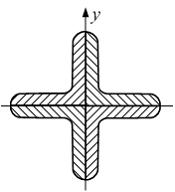
 ЗАДАНИЕ N 25 отправи Тема: Моменты инерции простых и сложных сечений  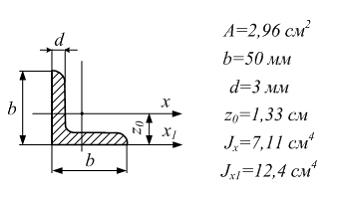 Поперечное сечение стержня составлено из четырех равнобоких уголков. Характеристики поперечного сечения уголка известны. Осевой момент инерции поперечного сечения относительно оси y равен ____ 

			49,6
			28,44
			20,9
			52,7

  ЗАДАНИЕ N 26 отправ Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей 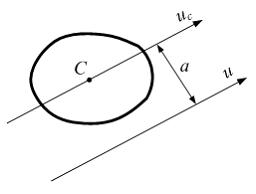На рисунке показана фигура, где   – площадь фигуры, – момент инерции площади фигуры относительно оси и,  – расстояние между осями. Момент инерции площади фигуры относительно оси   проходящей через центр тяжести, равен ____ см⁴.

			1750
			2250
			2050
			1950

Решение: Формула, связывающая моменты инерции относительно параллельных осей, одна из которых центральная, имеет вид  После вычислений получаем 

  ЗАДАНИЕ N 27 отправ Тема: Главные оси и главные моменты инерциим Центробежный момент инерции может быть величиной …

			положительной, отрицательнойя или равной нулю
			положительной или равной нулю
			отрицательной или равной нулю
			положительной

Решение: Центробежный момент инерции определяется интегралом 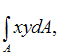  где А – площадь фигуры (см. рисунок). Координаты центра тяжести элементарной площади входят в подинтегральное выражение в первой степени. Следовательно центробежный момент инерции может быть величиной положительной, отрицательной или равной нулю.

 ЗАДАНИЕ N 28 отправ Тема: Статические моменты. Центр тяжести плоской фигуры Площадь фигуры   Статические моменты площади:    Координаты центра тяжести фигуры   

			–1,5; 3,5
			1,5; 3,5
			2; 4
			0,29; –0,67

 ЗАДАНИЕ N 29 отправи Тема: Перемещение и деформация На рисунке показано положение двух точек В и С до приложения к телу внешней нагрузки. После нагружения тела точки перемещаются в новое положение   и   Расстояние S между точками изменяется на величину   Линейная деформация в точке В по направлению отрезка ВСопределяется как …

  ЗАДАНИЕ N 30 отправит Тема: Основные понятия, определения, допущения и принципы Напряжение − это сила, …

			приходящаяся на единицу площади сечения
			приложенная к каждой единице объема тела
			приложенная к каждой единице площади поверхности тела
			приложенная к точке поверхности тела

Решение: 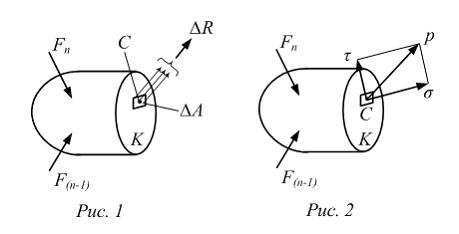На рисунке 1 показана отсеченная часть тела, находящаяся в равновесии под действием внешних сил и внутренних дополнительных усилий, действующих в каждой точке сечения К. ∆R – равнодействующая внутренних усилий, действующих по площадке с площадью ∆А.  – полное напряжение в точке С сечения К. Из структуры формулы видно, что напряжение − это сила, приходящаяся на единицу площади сечения. Полное напряжение обычно раскладывается на нормальное σ и касательное τ (рис.  2).

 ЗАДАНИЕ N 31 отправить с Тема: Модели прочностной надежности Моделью формы купола цирка является …

			оболочка
			стержень
			массивное тело
			пластина

 ЗАДАНИЕ N 32 отправи Тема: Внутренние силы и напряжения Полное напряжение в точке сечения определяется как …

(7)

 ЗАДАНИЕ N 1 отправит Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности Условие прочности по теории наибольших касательных напряжений имеет вид …

  ЗАДАНИЕ N 2 отправ Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) На рисунке показан элементарный объем и напряжения на его гранях. Главные напряжения: 

			40, 0, 0
			20, 0, -20

Решение: Верхняя грань элементарного объема является главной площадкой с главным напряжением, равным нулю. Два других главных напряжения определим по формуле 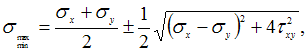  где (см. рисунок, вид сверху на элементарный объем):     Подставляя числовые значения в формулу для главных напряжений, получаем    Присваивая главным напряжениям индексы, имеем:     

  ЗАДАНИЕ N 3 отправит Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями На рисунке показан элементарный параллелепипед и напряжения на его гранях. Модуль упругости  , коэффициент Пуассона  . Деформация в направлении 1-1 равна …

Решение: 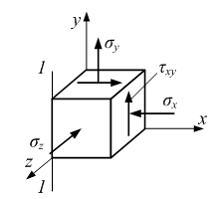В системе координат xyz:  ,  ,   Направление 1-1 параллельно оси y. Поэтому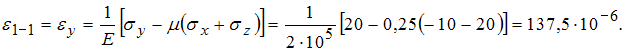 

 ЗАДАНИЕ N 4 отп Тема: Виды напряженного состояния На рисунке показана ферма нагруженная силой F. Напряженное состояние в точках стержней …

			линейное
			объемное
			плоское (чистый сдвиг)
			плоское

 ЗАДАНИЕ N 5 о Тема: Расчет на прочность при кручении 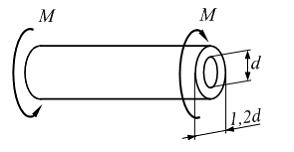Труба скручивается двумя моментами. Величины М и   заданы. Минимально допустимое значение параметра d  из расчета на прочность по допускаемым напряжениям равно …