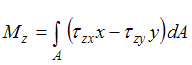Задание n 30
Тема:
Чистый сдвиг. Расчет на сдвиг
(срез)
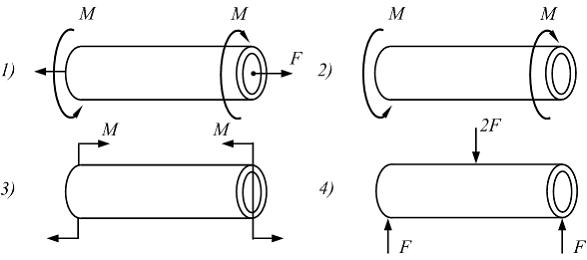Напряженное
состояние «чистый сдвиг» имеет место
при нагружении тонкостенной трубки по
схеме, показанной на рисунке …
|
|
|
2 |
|
|
|
1 |
|
|
|
4 |
|
|
|
3 |
Решение:
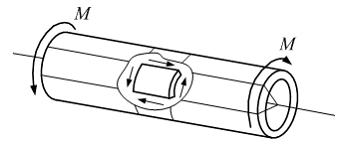Двумя
поперечными и двумя продольно-осевыми
сечениями выделим элемент стенки трубки
(см. рис.). Известно, что в поперечном
сечении трубки при кручении действуют
касательные напряжения. По закону
парности такие же напряжения действуют
в продольно-осевых сечениях.
Нормальные напряжения в этих сечениях
равны нулю. Поэтому напряженное состояние
стенки трубки – «чистый сдвиг».
ЗАДАНИЕ
N 31
Тема:
Расчет на жесткость при кручении
На
рисунке показан вал, скручиваемый
моментами 
Величины 
и 
известны.
Если
− допустимый
угол закручивания, то максимальное
касательное напряжение в поперечном
сечении вала равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 32
Тема:
Крутящий момент. Деформации и
напряжения
Стержень
скручивается моментом М.
Образующая АВ занимает
положение 
.
Углом сдвига является угол …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)
ЗАДАНИЕ
N 1
Тема:
Перемещение и деформация
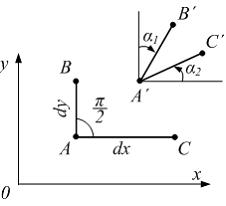В
процессе деформации точки А, В, С деформируемого
тела перемещаются в плоскости xoy и
занимают положения 
.
Прямолинейные отрезки АВ иАС поворачиваются
на углы 
и 
Угловая
деформация в точке А между
направлениями АВ и АС,
когда длины отрезков стремятся к нулю,
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Угловая
деформация – это изменение угла между
двумя взаимно перпендикулярными до
деформации малыми отрезками, проходящими
через данную точку. Следовательно,
угловая деформация в точке А между
направлениями АВ и АС равна 
ЗАДАНИЕ
N 2
Тема:
Внутренние силы и напряжения
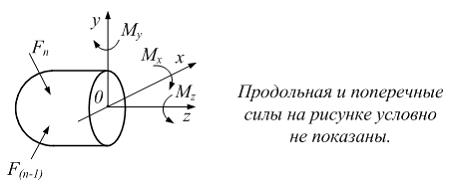Интегральная
связь между крутящим моментом 
(
)
и касательными напряжениями имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
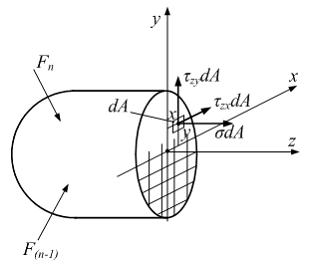Площадь
сечения можно разбить прямоугольной
координатной сеткой на элементарные
площадки. 
и 
–
равнодействующие касательных напряжений,
действующих на элементарной
площадке, 
− элементарные
моменты относительно оси z.
Крутящий
момент
определяется
как сумма элементарных моментов. Заменяя
суммирование интегрированием по площади
сечения, получаем 
ЗАДАНИЕ N 3 Тема: Основные понятия, определения, допущения и принципы Тело не разрушается под воздействием внешних сил, если его материал обладает свойством …
|
|
|
прочности |
|
|
|
упругости |
|
|
|
жесткости |
|
|
|
пластичности |
Решение: Все материалы обладают способностью сопротивляться разрушению под воздействием внешних сил. Это свойство материалов называется прочностью.
ЗАДАНИЕ N 4 Тема: Модели прочностной надежности Колонна здания относится к классу …
|
|
|
стержней |
|
|
|
оболочек |
|
|
|
массивов |
|
|
|
пластин |
ЗАДАНИЕ
N 5
Тема:
Моменты инерции простых и сложных
сечений
Осевой
момент инерции фигуры (см. рисунок)
относительно оси x равен ____ 
|
|
|
0,185 |
|
|
|
0,96 |
|
|
|
0,231 |
|
|
|
0,305 |
Решение:
Сложную
фигуру разделим на простейшие
(равносторонний треугольник и
прямоугольник).
Моменты
инерции:
треугольника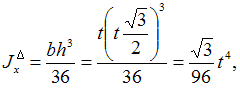 
прямоугольника 
всей
фигуры 
ЗАДАНИЕ
N 6
Тема:
Статические моменты. Центр тяжести
плоской фигуры
Координаты
центра тяжести фигуры (см. рисунок)
в заданной системе координат равны: 
|
|
|
4; 3,5 |
|
|
|
0; 4 |
|
|
|
0; 3 |
|
|
|
3,5; 5 |
ЗАДАНИЕ
N 7
Тема:
Осевые моменты инерции. Зависимость
между моментами инерции при параллельном
переносе осей
Осевой
момент инерции поперечного сечения
двутавра №10 относительно
оси 
равен ___ 
Характеристики
двутавра взять из ГОСТа.
|
|
|
498 |
|
|
|
300 |
|
|
|
258 |
|
|
|
320 |
Решение:
Для
определения осевого момента инерции
относительно оси
используем
формулу параллельного
переноса.
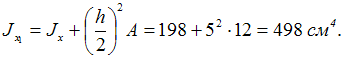Значения 
h и А взяты
из ГОСТа.
ЗАДАНИЕ N 8 Тема: Главные оси и главные моменты инерциим Размерность центробежного моменты инерции …
|
|
|
длина4 |
|
|
|
длина3 |
|
|
|
длина2 |
|
|
|
длина5 |
Решение:
Центробежный
момент инерции определяется интегралом 
Из
структуры подинтегрального выражения
видно, что размерность центробежного
момента инерции длина4.
ЗАДАНИЕ
N 9
Тема:
Механические свойства и механические
характеристики материалов
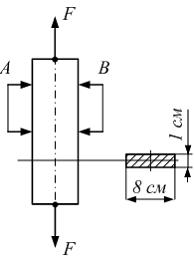При
нагружении образца прямоугольного
сечения силами 
стрелки
тензометров А и В переместились на 6 и
4 деления соответственно. Базы тензометров
– 20 мм.
Цена деления шкалы тензометров –
0,001 мм.
Модуль упругости материала образца
равен ____ МПа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Продольную
линейную деформацию центрального слоя
определим по формуле 
где А и В –
показания тензометров в числе делений, К –
цена деления шкалы тензометров, l –
размер базы тензометров. Подставляя
числовые значения, получаем 
Напряжение
в поперечном сечении образца 
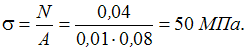Модуль
упругости материала образца 
ЗАДАНИЕ
N 10
Тема:
Испытание конструкционных материалов
на растяжение и сжатие
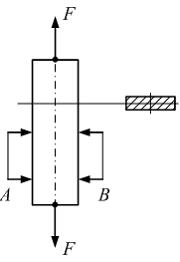При
определении модуля упругости
материала Е используется
образец в виде узкой полосы растягиваемой
силами F (см. рисунок).
Для измерения продольной деформации к
образцу крепятся не один, а два
тензометра А и В с
целью …
|
|
|
исключить влияние эксцентриситета приложения нагрузки и неправильности формы образца на результаты испытаний |
|
|
|
устранения возможной ошибки наблюдателя при отсчете показаний тензометров |
|
|
|
проверки точности показаний одного из тензометров |
|
|
|
исключить влияние качества материала образца на результаты испытаний |
Решение: Крайние слои образца удлиняются на разные величины. По результатам испытаний определяется удлинение центрального слоя как среднее арифметическое показаний тензометров. Тем самым исключается влияние эксцентриситета приложения нагрузки и неправильности формы образца на результаты испытаний.