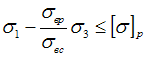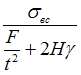ЗАДАНИЕ N 1  Тема: Модели прочностной надежности Колонна здания относится к классу …

			стержней
			оболочек
			массивов
			пластин

 ЗАДАНИЕ N 2  Тема: Перемещение и деформация 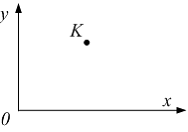Точка К деформируемого тела перемещается в плоскости xoy. Полное перемещение равно 5 мм. В направлении оси y точка переместилась на величину 3 мм. Перемещение точки в направлении оси x равно ____ мм.

			4
			2

 ЗАДАНИЕ N 3  Тема: Основные понятия, определения, допущения и принципы Древесина – материал …

			анизотропный
			кристаллический
			изотропный
			аморфный

 ЗАДАНИЕ N 4  Тема: Внутренние силы и напряжения Полное напряжение в точке сечения определяется как …

  ЗАДАНИЕ N 5  Тема: Главные оси и главные моменты инерции Главные центральные моменты инерции фигуры, состоящей из двух швеллеров №10, равны: 

			348; 258,5
			232; 155
			482; 368,7
			183,3; 128

Решение: 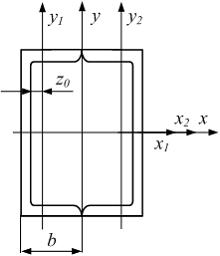Из таблицы ГОСТов берем характеристики швеллера №10:  Фигура имеет две оси симметрии x, y. На пересечении этих осей расположен центр тяжести фигуры, а оси симметрии являются главными центральными осями. Разделим фигуру на два швеллера. Оси x₁, x₂, y₁, y₂ являются главными центральными осями швеллеров. Тогда можно записать Подставляя числовые значения, получаем

 ЗАДАНИЕ N 6  Тема: Моменты инерции простых и сложных сечений 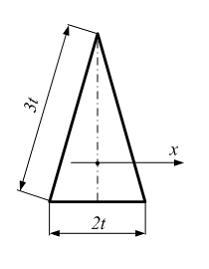Момент инерции равнобедренного треугольника относительно оси x, проходящей через центр тяжести параллельно основанию, равен …

 ЗАДАНИЕ N 7  Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Момент инерции площади – величина …

			положительная
			положительная или равна нулю
			положительная или отрицательная
			отрицательная или равна нулю

 ЗАДАНИЕ N 8  Тема: Статические моменты. Центр тяжести плоской фигуры 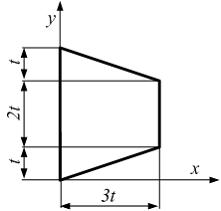В системе координат xy координата центра тяжести трапеции по оси x равна ___ t.

			1,33
			1,67
			1,1
			1,4

 ЗАДАНИЕ N 9  Тема: Расчет балок на прочность Консольная балка длиной   нагружена силой F. Сечение прямоугольное с размерами b и h. В сечении I-I максимальное нормальное напряжение равно   Предел текучести для материала балки   задан. Коэффициент запаса прочности по нормальным напряжениям равен …

 ЗАДАНИЕ N 10  Тема: Напряжения в поперечном сечении стержня при плоском изгибе  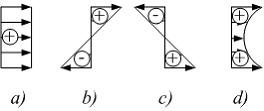    Эпюра распределения нормальных напряжений при чистом изгибе балки, показанной на схеме, имеет вид …

			b
			a
			c
			d

 ЗАДАНИЕ N 11  Тема: Поперечная сила, изгибающий момент и их эпюры 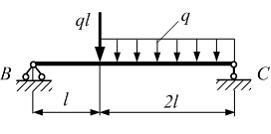Однопролетная балка ВС длиной   нагружена силой   и равномерно распределенной нагрузкой интенсивности q. Максимальные значения изгибающего момента и поперечной силы по абсолютной величине соответственно равны …

  ЗАДАНИЕ N 12  Тема: Перемещения при изгибе. Расчет балок на жесткость 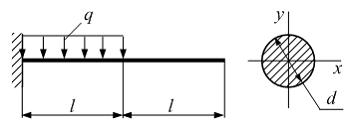Консоль на половине длины нагружена равномерно распределенной нагрузкой интенсивности   Модуль упругости материала балки   размер   Прогиб на свободном конце консоли не должен превышать  Из условия жесткости диаметр поперечного сечения d равен ____ (см).

			37,1
			18,5
			42,4
			28,4

Решение: Составим расчетную схему 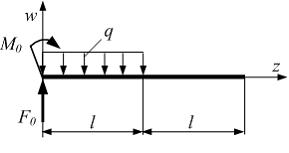Расположим начало координат в крайнем левом сечении балки и запишем универсальное уравнение упругой линии балки  где   и   – прогиб и угол поворота в начале координат; ,   – значения момента и силы в начале координат. Из условий равновесия балки определим Прогиб и угол поворота в начале координат   Подставим полученные значения в уравнение упругой линии Прогиб свободного конца консоли 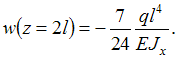Знак «минус» показывает, что прогиб направлен вниз. Из условия жесткости 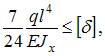  где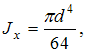  получим  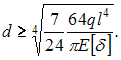После вычислений найдем

 ЗАДАНИЕ N 13  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Число компонент, полностью описывающих деформированное состояние в точке, в общем случае равно …

			шести
			трем
			четырем
			пяти

  ЗАДАНИЕ N 14  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) 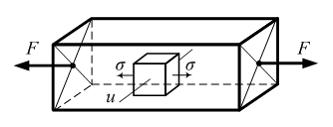На рисунке показан стержень, растянутый силами F, и элементарный объем выделенный гранями, параллельными плоскостям стержня. При повороте элементарного объема вокруг оси «u» на угол, равный 45⁰, напряженное состояние …

			не изменится
			становится плоским
			становится объемным
			становится плоским (чистый сдвиг)

Решение: На рисунке элементарный объем выделен главными площадками. Главные напряжения:   Напряженное состояние – линейное. Вид напряженного состояния не зависит от пространственной ориентации элементарного объема и при любом угле поворота остается линейным.

  ЗАДАНИЕ N 15 Тема: Виды напряженного состояния На рисунке показан стержень, работающий на кручение с растяжением. Напряженное состояние в точке К является – …

			линейное
			плоское
			объемное
			плоское (чистый сдвиг)

Решение: В точке К поперечного сечения действует нормальное напряжение от силы F. Эпюра касательных напряжений от крутящего момента показана на рисунке 1. В угловых точках   Поэтому напряженное состояние в точке К − линейное (одноосное растяжение, рис. 2).

  ЗАДАНИЕ N 16  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности Условие разрушения по теории прочности Мора имеет вид …

Решение: Условие разрушения по теории прочности Мора имеет вид   где   и   – пределы прочности на растяжение и сжатие,   и   – главные напряжения.

  ЗАДАНИЕ N 17  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина Однопролетная двухконсольная балка нагружена силой и моментом. Жесткость поперечного сечения на изгиб   по длине постоянна. Линейный размер lзадан. Прогиб сечения С от внешней нагрузки по абсолютной величине равен… (Влиянием поперечной силы на величину перемещения пренебречь).

Решение: Балка состоит из прямолинейных участков с постоянной жесткостью. Для определении прогиба сечения С используем интеграл Мора, который целесообразно вычислить по способу Верещагина. Построим эпюру изгибающих моментов от внешней нагрузки (рис. 1б). Эпюра построена на сжатом слое. 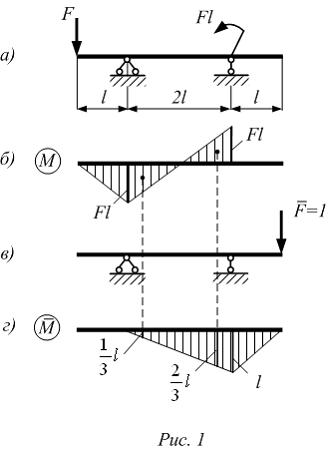К сечению С, прогиб которого определяем, прикладываем единичную силу  , а внешнюю нагрузку снимаем (рис. 1в). Строим эпюру изгибающих моментов от единичной силы. Используя технику перемножения эпюр, находим Знак «минус» показывает, что сечение С перемещается в направлении, противоположном направлению единичной силы – вверх.

  ЗАДАНИЕ N 18 Тема: Расчет простейших статически неопределимых систем На рисунке показан стержень нагруженный силами F и моментами М. Размер l, диаметр d, модули упругости Е и G заданы. Крутящий момент и продольная сила в сечении С-С, соответственно, равны …

			0, 0

Решение: Стержень геометрически симметричен относительно плоскости симметрии С-С. Нагрузим стержень поочередно моментами М и силами F (рис. 1, 2). В первом варианте (рис. 1) стержень нагружен симметричной нагрузкой. Следовательно в сечении С-С кососимметричный внутренний силовой фактор, крутящий момент, равен нулю. Во втором варианте (рис. 2) стержень  нагружен кососимметричной нагрузкой. Следовательно, в сечении С-С симметричный внутренний силовой фактор, продольная сила, равен нулю. Таким образом, в сечении С-С и во всех сечениях среднего грузового участка крутящий момент и продольная сила равны нулю.

 ЗАДАНИЕ N 19  Тема: Статическая неопределимость. Степень статической неопределенности Степень статической неопределимости плоской рамы равна …

			четырем
			трем
			пяти
			двум

Задание n 20 Тема: Метод сил

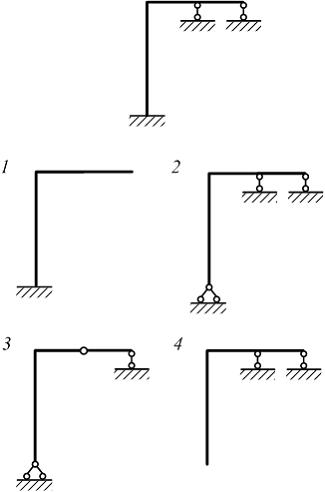Для статически неопределимой системы один из вариантов правильно выбранной основной системы показан на рисунке …

			1
			2
			3
			4

 ЗАДАНИЕ N 21  Тема: Расчеты стержней на прочность и жесткость 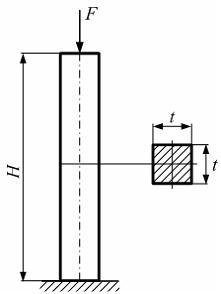Колонна находится под действием собственного веса и силы F, приложенной в центре тяжести поперечного сечения (см. рисунок). Известны величины: F, H,t,   – объемный вес материала колонны,   – предел прочности на сжатие. Выражение для коэффициента запаса прочности имеет вид …

 ЗАДАНИЕ N 22  Тема: Механические свойства и механические характеристики материалов Для хрупких материалов за опасное (предельное) напряжение принимается предел …

			прочности
			пропорциональности
			текучести
			выносливости

 ЗАДАНИЕ N 23  Тема: Продольная сила. Напряжения и деформации Продольная сила есть равнодействующая …

			нормальных напряжений в поперечном сечении стержня
			внешних сил, приложенных к отсеченной части стержня
			нормальных напряжений и внешних сил, приложенных к отсеченной части стержня
			всех внешних сил, приложенных к стержню

 ЗАДАНИЕ N 24  Тема: Испытание конструкционных материалов на растяжение и сжатие 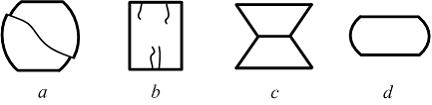Вид образца из пластичного материала после испытаний на сжатие показан на рисунке …

			d
			a
			b
			c

Задание n 25

Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Наименьшему значению критической силы соответствует форма потери устойчивости, показанная на рисунке …

			а
			г
			б
			в

Решение: Стержень, жестко защемленный одним концом и нагруженный осевой сжимающей силой на другом, находится в таких же условиях, как стержень шарнирно-закрепленный по обоим концам. Поэтому, наименьшему значению критической силы соответствует форма потери устойчивости, показанная на рисунке «а».