3.2 Экспоненциальная функция из r в r
Рассмотрим задачу Коши
,
,
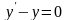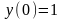(3.4)
где
;
.
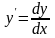Согласно
теореме 3.1, эта задача имеет единственное
решение, определенное и дифференцируемое
(а значит, непрерывное) на всей числовой
прямой. Обозначим его
.
Из тождества
,
следует, что функция
бесконечно дифференцируема на
,
причем
,
(
).
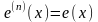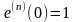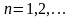Функция обладает также следующими свойствами.
Функция положительна.
Функция возрастает.
Действительно,
так как
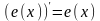и
на R,
на
и, следовательно, функция
возрастает.
(Теорема сложения для функции ). Справедливо соотношение
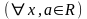(3.5)
4.
.
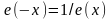
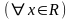5.
,
.
6. Функция разлагается на промежутке в ряд Маклорена:
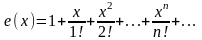
7.
.
Замечание
1:
Так
как очевидно, что функция
также является решением задачи Коши
(3.4), то
.
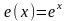32. Увядзенне элементарных функцый з дапамогай др. Трыганам.
Теорема 3.1: Дифференциальное уравнение
где ; ; ; , имеет на единственное n-кратно дифференцируемое решение , удовлетворяющее условиям
, , … ,
(здесь , , , … , - произвольно заданные фиксированные действительные числа).
Очевидно, что это решение обладает на непрерывными производными всех порядков.
В частности, когда , указанное в теореме 3.1 решение тривиально на ).
3.1 Тригонометрические функции из r в r
Рассмотрим следующие две задачи Коши:
синус
,
,
;
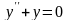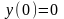(3.1)
косинус
,
,
;
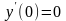(3.2)
где
;
;
.
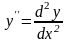Их решения обозначим соответственно
через
и
.
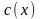Согласно теореме 3.1, эти решения
определены, непрерывны и бесконечно
дифференцируемы на всей числовой прямой,
причем
,
.
Однако основные свойства функций
,
установим, исходя из определения их как
решений задач (3.1) и (3.2).
1.
,
.
2. Функция нечетная, а четная.
3.
Имеет
место тождество
.
.
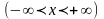4. Справедливы следующие соотношения (теоремы сложения для функций и ):
,
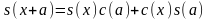(3.3)
,
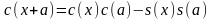Замечание:
Полагая
в формулах (3.3)
,
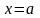получаем следующие формулы удвоения:
,
,
.
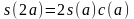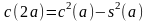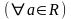Отсюда с учетом свойства 3 получаем:
,
,
.
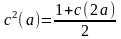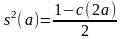Лемма 3.2: Функция имеет хотя бы один положительный нуль.
Замечание:
Если
,
то и
для любого
.
5. Существует наименьший положительный нуль функции .
6.
Функция
положительна на интервале
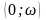и отрицательна на интервале
.
7.
Функция
убывает на
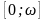и возрастает на
.
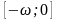8.
Числа
вида
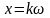
и только эти числа явл. нулями функции
.
9.
,
;
,
.
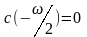10.
Функция
положительна на
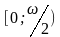и отрицательна на
.
11.
.
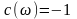12.
Функция
возрастает на
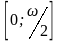и убывает на
.
13.
Функции
,
-
периодические с основным периодом
.
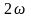14.
Нулями
функции
являются числа вида
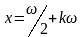и только эти числа.
15. Справедливы следующие тождества (формулы приведения):
,
,
,
,
,
,
,
,
,
,
,
,
,
.
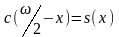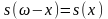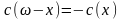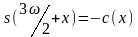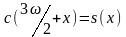16.
Наименьший положительный нуль функции
равен
.
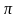