
- •2.Задачы, якия прыводзяцца да дыферэнцыяльных раунанняу.
- •3.Здр першага парадку: формы запису, рашэнни и интэгралы, геаметрычная интерпрытацыя частковага и агульнага рашэнняу.
- •4.Задача Кашы. Пункты иснавання и адзинасци рашэння. Умовы иснавання и адзинасци.
- •5.Агульныя, частковыя и асаблівыя рашэнні.
- •6.Метад изаклин для здр першага парадку
- •7.Др у поуных дыферэнцыялах. Прыкмета раунання у поуных дыферэнцыялах. Прыклады.
- •8.Др у поуных дыферэнцыялах. Интэгроуны множник. Прыклады
- •9.Др са зменными якия падзяляюцца, якия падзелены, раунанни якия да их прыводзяцца.
- •10.Аднародныя др (адносна зменных). Аднародныя функцыи
- •11. Др якия зводяцца да аднародных (адносна зменных)
- •12. Ладр першага парадку. Агульнае рашэнне
- •13. Ладр першага парадку. Структура агульнага рашэння. Метад Бернули
- •14. Рашэнне лндр першага парадку. Метад Лагранджа. Раунанне Бернули.
- •15.Тэарэма Пикара для здр першага парадку
- •16. Выкарыстанне прынцыпу сцискальных адлюстраванняу для доказу тэарэмы Пикара
- •18. Др якия дапускаюць панижэнне парадку.
- •§19. Лндр з пастаяннымі каэфіцыентамі.
- •20. Прастора рашэнняў ладр n-га парадку. Лінейная залежнасць і незалежнасць сістэмы функцый. Неабходная ўмова лінейнай залежнасці. Вранскіян. Дастатковая ўмова лінейнай незалежнасці. Прыклады.
- •22.Формула Астраградскага-Лиувиля
- •23. Дапаможныя звесткі
- •24.Ладр n-нага парадку з пастаянными каэфіцентамі. Характэрыстычнае раўнанне. Выпадкі розных сапраўдных каранёў і кратнага сапраўднага корня.
- •1 Выпадак
- •3 Выпадак
- •25. Ладр n-нага парадку з пастаянными каэфицентами. Характэрыстычнае раунанне. Выпадак каплекснага кораня.
- •2 Выпадак.
- •26. Ладр n-нага парадку з пастаянными каэфицентами и спецыяльнай правай часткай. Спецыяльная правая частка са здабыткам мнагаскладу и экспаненты.
- •27. Ладр n-нага парадку з пастаянными каэфицентами и спецыяльнай правай часткай. Спецыяльная правая частка са здабыткам экспаненты и синусам-косинусам.
- •28.Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вольныя ваганни у асяродзи без супрациулення.
- •29. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вольныя ваганни у асяродзи з супрациуленнем.
- •30. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вымушаныя ваганни у асяродзи без супрациулення.
- •31. Увядзенне элементарных функцый з дапамогай др. Экспанента
- •3.2 Экспоненциальная функция из r в r
- •32. Увядзенне элементарных функцый з дапамогай др. Трыганам.
- •3.1 Тригонометрические функции из r в r
- •33. Систэмы др. Астноуныя паняцци. Задача Кашы. Иснаванне и адзинасць рашэння. Агульныя и частковыя рашэнни.
- •34. Прывядзенне нармальнай систэмы да др н-нага парадку и наадварот.
- •35. Линейныя систэмы др. Лас и лнс. Линейная незалежнасць систэмы функцыянальных вектарау. Фундаментальная систэма. Вронскиян.
- •36. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Характэр. Раунанне. Паняцце аб метадзе Эйлера.
- •37. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак розных сапраудных каранёу.
- •38. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак розных каранёу сярод яких ёсць камплексныя.
- •39. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак, кали сярод каранёу сустракаюцца кратныя.
30. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вымушаныя ваганни у асяродзи без супрациулення.
Няхай дадзена цела масы m, якое падвешана на пружыне. Калі цела знаходзіцца ў становішчы раўнавагі, то сіла m*g ураўнаважваецца упругой сілай пружыны. Г.зн, што mg=сs, дзе с – каэфіцыент пругкасці. Вывядзем цела са становішча раунавагі: перамясцім цела на адлегласць у0 ад пачатковага становішча і адпусцім. Выберам накірунак восі уздоўж пружыны, а за пачатак каардынат возьмем пачатковае становішча цела. Становішча цела у момант часу t будзе апісваць функцыя y(t).
Выніковая усіх сіл: F = ma, F = mg - c(y+s) - ky’ = -cy - ky’, дзе k – каэфіцыент супраціулення асяроддзя.
a = y’’, my’’ = -cy - ky’, або my’’+ cy + ky’ = 0 (1). Гэта раунанне называецца раўнаннем свабодных ваганняў.
Калі прысутнічаюць нейкія знешнія сілы, тады раунанне прыме выгляд:
my’’+ky’+cy = Fзн(t) (2) і яно называецца раўнаннем вымушанных ваганняў у асяроддзі з супраціўленнем.
Для зручнасці раунанне (1) і (2) перапішам у выглядзе:
y’’+k/m*y’ +c/m*y = 0 Абазн: k/m = 2p c/m = w2
y’’+2py’ + w2 y = 0 (1’)
y’’+2py’ + w2 y = 1/m Fзн(t) (2’)
y’’+w2 y = 0 называецца раўнаннем вольных ваганняў у асяроддзі без супраціўлення.
Вымушаныя ваганни у асяродзи без супрациулення
Разгледзім раўнанне (2’) у выпадку, калі правая частка мае спецыяльны выгляд: 1/m Fзн(t) = H sin qt, дзе q, t – некаторыя лікі
y’’+2py’ + w2 y = H sin qt
Разгледзім выпадак вымушаных ваганняў у асяроддзі без супраціўлення. Гэта мадэль апісваецца раўнаннем y’’+ w2 y = H sin qt. Знойдзем частковае рашэнне гэтага раўнання метадам нявызначаных каэфіцыентаў
а) q ≠ w ỹ = M cos qt + N sin qt
P0(t) = 0 Q0(t) = H
ỹ‘ = -q M sin qt + q N cos qt
y ‘’ = -q2 M cos qt - q2 N sin qt
-q2 M cos qt - q2 N sin qt + w2(M cos qt + N sin qt) = H sin qt
-q2 M + w2M = 0 M = 0
-q2 N + w2N = 0 N = H/ (w2 - q2)
ỹy = H/ (w2 - q2) sin qt
y = A sin (wt + α) + H/ (w2 - q2) sin qt
У дадзеным выпадку маем 2 ваганні з рознымі частотамі, пры гэтым, калі w→ t, то y(t) будзе расці.
Гэта з’ява выкарыстоўваецца у радыепрыемніках.
б) q = w
Частковае рашэнне шукаем у выглядзе: ỹ = (M cos qt + N sin qt) t
ỹ‘ = (-q M sin qt + q N cos qt ) t + M cos qt + N sin qt
y ‘’ = (-q2 M cos qt - q2 N sin qt) t -2q M sin qt + q N sin qt + 2q N cos qt
(-q2 M cos qt - q2 N sin qt) t - 2q M sin qt + 2q N cos qt + w2 (M cos qt + N sin qt) t = H sin qt
-2qM = H M= –H/2q
2qN = 0 N = 0
ỹ = –H/2q t cos qt
y = A sin (wt + α) –H/2q t cos qt
У дадзеным выпадку маем сітуацыю, калі амплітуда другога складніка з цягам часу неабмежавана расце. Такая з’ява, калі пры t → 0, размахі ваганняў неабмежавана нарастаюць называецца зэявай рэзананс.
31. Увядзенне элементарных функцый з дапамогай др. Экспанента
Теорема 3.1: Дифференциальное уравнение
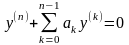
где
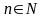 ;
;
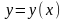 ;
;
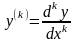 ;
;
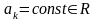
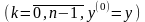 ,
имеет
на
,
имеет
на
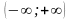 единственное n-кратно
дифференцируемое решение
единственное n-кратно
дифференцируемое решение
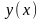 ,
удовлетворяющее условиям
,
удовлетворяющее условиям
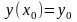 ,
,
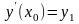 ,
… ,
,
… ,
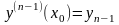
(здесь
,
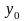 ,
,
… ,
,
,
… ,
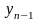 -
произвольно заданные фиксированные
действительные числа).
-
произвольно заданные фиксированные
действительные числа).
Очевидно, что это решение обладает на непрерывными производными всех порядков.
В
частности, когда
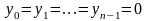 ,
указанное в теореме 3.1 решение тривиально
,
указанное в теореме 3.1 решение тривиально
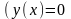 на
).
на
).
