1.Звычайныя ДР: азначэнне, парадак раунання, интегральныя крывыя, рашэнне раунання, интеграванне, интеграванне у квадратурах.

Няхай зададзена ф-цыя y=f(x). Няхай F – ф-цыя (n+2)-х зменных. Разгледзім 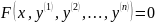(1), дзе F-вядомая ф-цыя, х – незалежная зменная, у=у(х) – невядомая ф-цыя.

Азн.1: Звычайным дыферэнцыяльным раўнаннем (ЗДР) наз.раўнанне (1), якое ўтрымлівае незал.зменную х, невядомую ф-цыю у(х), а так сама вытворныя ф-цыі у(х) да n-га парадку.

Азн.2: Парадкам ЗДР наз.парадак старэйшай вытворнай невядомай ф-цыі.

Заўвага 1: паняцце ўведзена ў 1676 годзе Лейбніцам.

Заўвага 2: ЗДР наз.таму, што яно ўтрымлівае звычайную вытворную ф-цыі 1-й незалежнай зменнай. Калі будзе ф-цыя некалькіх аргументаў, тады кажуць пра раўнанне ў частковых вытворных.

Прыклад 1: 1) 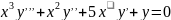- ЗДР 3-га парадку

2) 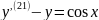- ЗДР 21-га парадку

Азн.3: Ф-цыя у=у(х) наз.рашэннем ЗДР (1) на некаторым прамежку I, калі 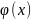n разоў непарыўна дыферэнцавальна на прамежку I і пры падстаноўцы ў (1) звяртае яе ў правільнае раўнанне.

Прыклад 2:

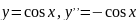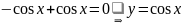. – рашэнне.

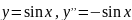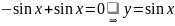. – рашэнне.

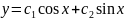- агульнае рашэнне.

Азн.4: Працэс знаходжання рашэння ЗДР наз.інтэграваннем ДР.

Азн.5: Графік рашэння ДР наз.інтэгравальнай крывой.

Заўвага 3: Калі задачу аб рашэнні ДР удаецца звесці да вылічэння канечнага ліку інтэгралаў і вытворных ад вядомых ф-цый і алгебраічных аперацый над імі, то кажуць, што ДР інтэгруецца ў квадратурах.

Прыклад 3: 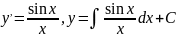. У тэорыі ДР пад выразам падразумяваецца адна першавобразная, а не сям`я першавобразных. Зыходнае раўнанне інтэгравальна ў квадратурах.

Задачай тэорыі ЗДР з`яўляецца знаходжанне рашэнняў ДР, даследване агульных ўл-сцей рашэнняў і развіцце дакладных асімптатычных і лікавых метадаў інтэгравання ДР.

2.Задачы, якия прыводзяцца да дыферэнцыяльных раунанняу.

Прыклады задач:

1) Рух цела масай m пад дзеяннем знешніх сіл.

Па 2-му закону Ньютана: ,

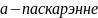
Няхай цела рухаецца уздоўж восі 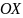і ў момант часу 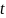яго становішча задаецца як 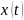. Згодна з фізічным сэнсам вытворнай: .

. З фізікі вядома: для таго, каб вызначыць становішча цела ў момант часу 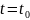, патрэбна ведаць .

2) Эвалюцыйная сістэма.

Саставіць раўнанне колькасці папуляцыі,калі вядома, што хуткасць росту папуляцыі прапарцыянальна колькасці папуляцыі.

Няхай - колькасць папуляцыі ў момант часу .

- хуткасць росту папуляцыі, - атрымана звычайнае ДР, якое апісвае колькасць папуляцыі у момант часу .

3.Здр першага парадку: формы запису, рашэнни и интэгралы, геаметрычная интерпрытацыя частковага и агульнага рашэнняу.

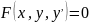(1) – агульны выгляд ЗДР 1-га парадку.

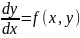(2), F(x,y) – ф-цыя, вызначаная ў некаторай вобласці ХОУ.

Раўнанне ЗДР 1-га парадку, выражанае адносна вытворнай.

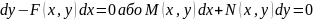(3)

(3) – дыферэнцыяльнае раўнанне 1-га парадку ў дыфер.форме.

або .

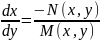Калі ф-цыя ў наваколлі некаторага пункту 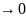, тады замест (2) разглядаюць перавернутае: .

Гэта таксама робяць, калі такое раўнанне рашаецца лягчэй, чым (2) 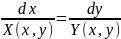- сіметрычна.

Разгледзім ДР 1-га парадку выгляду 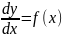(4). - агульнае рашэнне (4). Заўважым, што агульнае рашэнне (4) мае выгляд 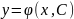. Зыходнае раўнанне (2) агульнае рашэнне будзе мець таксама ў такім выглядзе , С – нейкая адвольная пастаянная 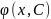- рашэнне ДР (2).

Рашэнне, якое атрымліваецца пры канкрэтным значэнні С, уключаючы 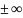, наз.частковым рашэннем. Калі рашэнне ДР (2) задаецца ў выглядзе неяўнай ф-цыі 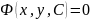, тады яно наз.агульным інтэгралам ДР.

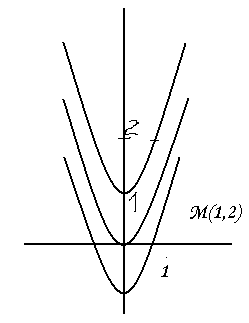
Прыклад1: На плоскасці ХОУ знайсці крывую, якая праходзіць праз пункт 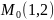і ў кожным пункце мае датычную, вуглавы каэфіцыент якой = падвоенай абсцысе пункта дотыку. M(x,y).

Калі задача Кашы мае адзінае рашэнне, то гэта азначае, што калі існуе 2 рашэнні , якія з`яўл.рашэннямі задачы Кашы (2), (5), то г.зн. .

Упершыню ўмовы на існаванне яе адзінасці былі прапанавапны Кашы ў 1820-30-х гг. і дакакзаны ім.

4.Задача Кашы. Пункты иснавання и адзинасци рашэння. Умовы иснавання и адзинасци.

Разгледзім ДР (2) . Калі нам патрэбна з агульнага рашэння выдзеліць нейкае адно рашэнне, якое здавальняе пачатковай ўмове (5), то кажуць, што нам трэба рашыць задачу Кашы. Т.ч. ДР (2) з пачатковай умовай (5) наз. задачай Кашы.

Прыклад1: На плоскасці ХОУ знайсці крывую, якая праходзіць праз пункт і ў кожным пункце мае датычную, вуглавы каэфіцыент якой = падвоенай абсцысе пункта дотыку. M(x,y).

Калі задача Кашы мае адзінае рашэнне, то гэта азначае, што калі існуе 2 рашэнні , якія з`яўл.рашэннямі задачы Кашы (2), (5), то г.зн. .

Упершыню ўмовы на існаванне яе адзінасці былі прапанавапны Кашы ў 1820-30-х гг. і дакакзаны ім.

Тэарэма Пікара: Нях. дадзена ДР (1) з пачатковымі ўмовамі (2). Калі ф-я f(x;y) задавальняе 2-м умовам:

1) f – непар. па абедзьвух зменных х і у ў замкненым абсягу , дзе a і b дадзеныя дадатныя лікі. Тады .

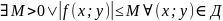2) Ф-я f(х;у) задавальняе ўмове Ліпшыца па другой зменнай, г.зн. для ўсіх пунктаў (х;у) Д, дзе L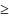 0 – пастаянная Ліпшыца. Тады адзінае рашэнне у(х) ДР (1), якое задавальняе пачатковай умове (2) і якое вызначана і непарыўна дыф-нае для ўсіх 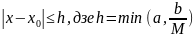і якое належыць Д для гэтых х.

Заўвага: Для выканання ўмовы Ліпшыца дастаткова, каб частк. вытв. Па 2-й зменнай была абмежаваная.

Доказ:

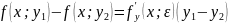знаходзіцца паміж .

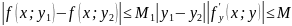
Даказана.