3.2. Розрахунок параметрів ребристого радіатора в режимі вільної конвекції

Дано: P = 13.5 Вт; R_ПК = 2,5 К/Вт; R_KP =0.4 К/Вт; t_ПM = 140 °С; t_C = 25 °С;

ε = 0.8; λ = 210 Вт/К.

1. Розглянемо рівняння:

t_П – t_C = (t_П – t_K) + (t_K – t_P) + (t_P – t_C). (1)

З урахуванням того, що

θ_ПK = t_П – t_К = Φ R_ПK, (2)

θ_KР = t_К – t_Р = Φ R_KР,

рівняння набуває вигляду

t_Р = t_П - Φ (R_ПK + R_КР).

Згідно даним і врахувавши, що Φ = P, одержимо максимальну температуру радіатора в місці кріплення НПП:

t_Р = 140 – 13.5 (2.5 + 0.4) = 100.85 °C.

2. Згідно таблиці 1 [1] в першому наближенні приймаємо, що коефіцієнт К_НР =0.96, тобто попередньо орієнтуємося на розмір L = 80 ∙ 10^-3 м. Отже в першому наближенні площа квадратної основи радіатора А^І = 6400 ∙ 10^-6 м², а густина теплового потоку

 = 2.1 ∙ 10³ Вт/м².

Згідно [1] перегрів радіатора дорівнює

θ_SC = t_S – t_C = [(t_П – t_C) - Φ (R_ПК + R_KP)] ∙ K_HP = (t_P – t_C) ∙ K_HP =

= (100.85 - 25) ∙ 0.96 = 72.82 °C.

Середній перегрів θ_SC вийшов за допустимі межі графіків на рис. 7 [2]. Тому робимо друге наближення, приймаючи K_HP = 0.86. Тоді L = 160 ∙ 10^-3 м, А^ІІ = 0.0256 м²,

 = 0.527 ∙ 10³ Вт/м².

θ_SC = (t_P – t_C) ∙ K_HP = (100.85 - 25) ∙ 0.527 = 39.97 °C.

Згідно графіків (рис. 7) [2] значення q =0.527 Вт/м² при θ_SC= 40 °С попадає в область, що відповідає ребристому радіатору при вільній конвекції.

3. З конструктивних міркувань приймаємо:

форма основи – квадрат (L×L = А),

L = 160 ∙ 10^-3 м,

α_еф = = 21.6 Вт/м²К,

площа основи А = 0.015625 м².

Основа радіатора з однієї сторони має ребра, з іншої сторони кріпиться НПП. Ребристий радіатор встановлюємо у вертикальному положенні, канали між ребрами направлені теж вертикально.

4. Згідно рис. 8,а [2] даному типу радіатора при α_еф = 21.6 Вт/м²К та θ_S= 40 °С відповідає зона 11. Тоді вибираємо наступні розміри ребер:

• висота ребра h = 12.5 мм;

• крок ребер b = S^//_ш = 5 мм;

• товщина ребра δ = δ₁ = 1 мм;

• довжина ребер L = 125 мм.

5. Кількість тепла, що конвективно віддається поверхнями ребер радіатора, визначається формулами:

,

,

де N – кількість ребер радіатора;

λ – коефіцієнт теплопровідності матеріалу ребра, Вт/мК;

A_p – площа поперечного перерізу ребра, м;

θ₁ – перегрів основи радіатора;

α_K – коефіцієнт конвективної тепловіддачі, Вт/м²К.

Заданими є значення λ та h. Визначимо:

A_p = L ∙ δ = 125 ∙ 10^-3 ∙ 1 ∙ 10^-3 = 0.125 ∙ 10^-3 м².

.

Приймаємо N = 22.

,

де t_p – ще невідоме.

Значення m теж неможливо визначити, бо треба знайти спочатку α_K. Значення α_K краще шукати в залежності від перегріву θ₁ з допомогою теплових характеристик. Це краще робити з врахуванням радіаційної складової α_в.

6. Теплопередача шляхом випромінювання при перегріві θ_PC = t_S - t_C визначається формулою

Φ_в = α_вA_в(t_S - t_C),

де А_в – площа поверхні випромінювання радіатора;

A_в = 2L [(N - 1)(b + δ) + δ] + 2h L N = 2 ∙ 125 ∙ 10^-3 [(22 – 1)(5 + 1) ∙ 10^-3 + 10^-3] + 2 ∙ 12.5 ∙ 10^-3 ∙ 125 ∙ 10^-3 ∙ 22 = 0.1 м²;

t_S – середня температура ребра радіатора,

і поки що не може бути визначеною.

Коефіцієнт тепловіддачі випромінюванням

α_В = ε ψ f(t_S, t_C),

де ε – приведена ступінь чорноти, дано ε = 0.8;

ψ – коефіцієнт опромінювання

.

Функція f(t_S, t_C) визначається згідно таблиці.

7. Переходимо до визначення теплової характеристики радіатора Φ = Φ(θ_S).

7.1. Задаємося значенням перегріву основи радіатора θ₁ = 20 °C. Тоді температура радіатора

t_P = t_C + θ₁ = 25 + 20 = 45 °C.

Середня температура прошарку повітря навколо ребра

t_m = 0.5 (t_P + t_C) = 0.5(45 + 25) = 35 °C.

Оскільки ребро і канали між ребрами розташовані вертикально, то визначальний розмір конвективного теплообміну

L = L₁ = 125 ∙ 10^-3 м.

Оскільки

то степінь закону кондуктивного теплообміну n = 1/3.

Коефіцієнт конвективної тепловіддачі ребра

α_K = a₃∙N∙ = 1.55 ∙ 1 ∙ 20^1/3 = 4.21 Вт/м²К.

Коефіцієнт a₃ визначений з таблиці.

Характеристичний параметр ребра

.

Периметр поперечного перерізу ребра

U = 2(L + δ) = 2 (125 + 1) ∙ 10^-3 = 0.25 м.

Площа поперечного перерізу ребра

A_P = Lδ = 125 ∙ 10^-3 ∙ 1 ∙ 10^-3 = 0.125 ∙ 10^-3 м².

Тому при θ₁ = 20 °С

= 6.33 м^-1.

Конвективна складова потужності теплового потоку радіатора

=

= 22 ∙ 210  ∙ 6.33  ∙ 0.125 ∙ 10^-3 ∙ 20 ∙ 0.0793 = 5.80 Вт.

Було враховано, що

mh = 6.36 ∙ 12.5 ∙ 10^-3 = 0.0795,

а th(mh) = th(0.0795) = 0.0793.

Визначимо середню температуру ребра радіатора

= 44.93 °С ≈ 45 °С.

Було враховано, що

.

Скориставшись таблицею знаходимо, що

f(t_S, t_C) = f(45, 25) = 6.66.

Коефіцієнт тепловіддачі випромінюванням

α_В = εψ f(t_S, t_C) = 0.8 ∙ 0.17 ∙ 6.66 = 0.905 Вт/м²К.

Радіаційна складова теплового потоку радіатора при θ₁=20 °С або при t_S = 45 °С дорівнює

Φ_В = α_В A_В(t_S - t_C) = 0.905 ∙ 0.1 ∙ 20 = 1.81 Вт.

Таким чином, при θ_SC = 20 °С або θ_P = 45 °C сумарний тепловий потік радіатора

Φ = Φ_K + Φ_В = 5.80 + 1.81 = 7.61 Вт.

7.2. Задаємося перегрівом основи радіатора θ₁= 40 °C.

Температура радіатора

t_P = t_C + θ₁ = 25 + 40 = 65 °C.

Середня температура прошарку повітря навколо ребра

t_m = 0,5(t_P + t_C) = 0.5(65 + 25) = 45 °C.

Степінь закону кондуктивного теплообміну згідно тієї ж самої нерівності n =1/3.

Конвективний коефіцієнт тепловіддачі

α_K = a₃∙N∙ = 1.49 ∙ 1 ∙ 45^1/3 = 5.30 Вт/м²К.

Характеристичний параметр

= = 7.10 м^-1.

Тепловий конвективний потік

=

= 22 ∙ 210  ∙ 7.1  ∙ 0.125 ∙ 10^-3 ∙ 20 ∙ 0.088 = 7.26 Вт.

Враховано, що при mh = 0.089, th(0.089) = 0.0885.

Середня температура ребра

= 64.9 °С ≈ 65 °С.

Враховано, що ch(mh) = 1.0039.

f(t_S, t_C) = f(65, 25) = 7.37.

Коефіцієнт тепловіддачі випромінюванням

α_В = εψ f(t_S, t_C) = 0.8 ∙ 0.17 ∙ 7.37 = 1.00 Вт/м²К.

Тепловий радіаційний потік

Φ_В = α_В A_В(t_S - t_C) = 1.00 ∙ 0.1 ∙ 40 = 4.00 Вт.

Сумарний тепловий потік при θ₁ =40 °C

Φ = Φ_K + Φ_В = 7.81 + 4.00 = 11.01 Вт.

7.3. Будуємо теплову характеристику радіатора по трьох точках:

θ₀ = 0 °C, Φ₀ = 0 Вт;

θ₁ = 20 °C, Φ₁ = 7.61 Вт;

θ₂ = 40 °C, Φ₂ = 11.01 Вт.

Рис. 1. Теплова характеристика радіатора

Знаючи потужність НПП Р = Φ = 13.5 Вт, знаходимо з допомогою теплової характеристики справжній нагрів основи радіатора: θ₁ = 55 °C.

Температура радіатора в місці кріплення НПП

t_P = θ₁ + t_C = 55 + 25 = 80 °C.

Температура p-n переходу НПП

t_П = t_P + Φ (R_ПК + R_KP) = 80 + 13.5(2.5 + 0.4) = 119.15 °C,

що менше гранично допустимої t_ПМ =140 °С. Радіатор задовольняє основній умові задачі. Отже потужність 13.5 Вт вибраний радіатор відводить при t_P =80 °C, t_П =119.15 °C.

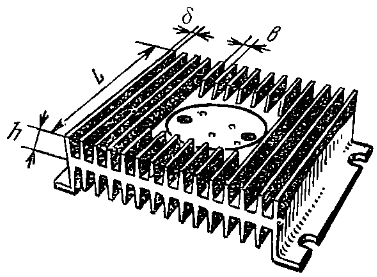
Рис.2. Ребристий радіатор Рис. 3. Ребристий радіатор у складі

процесорного кулера