
1.7 Эвристический поиск
Поскольку слепой поиск возможен только в небольшом пространстве вариантов, напрашивается совершенно естественный вывод, что необходим некоторый способ направленного поиска. Если такой способ использует при поиске пути на графе в пространстве состояний некоторые знания, специфические для конкретной предметной области, его принято называть эвристическим поиском. Т.е. при эвристическом поиске для выбора тех ветвей из пространства состояний, которые с наибольшей вероятностью приведут к приемлемому решению проблемы, используется совокупность правил.
Эвристика — это только предложение следующего шага, который будет сделан на пути решения проблемы. Лучше всего рассматривать эвристику в качестве некоторого правила влияния, которое, хотя и не гарантирует успеха (как детерминированный алгоритм или процедура принятия решения), в большинстве случаев оказывается весьма полезным.
Одним из самых распространенных эвристических алгоритмов поиска является восхождение на гору (hill climbing) или процедуре поиска экстремума. В процессе поиска в программе использует некоторая оценочная функция, с помощью которой можно грубо оценить, насколько "хорошим" (или "плохим") является текущее состояние. Затем можно применить ту же функцию для выбора очередного шага, переводящего систему в следующее состояние. При таком подходе задача поиска сводится к процедуре поиска экстремума оценочной функции.
Например, простая оценочная функция для программы игры в шахматы может включать очевидную оценку материала (количества и качества имеющихся на доске фигур) — своего и соперника. Затем программа перебирает возможные операторы перехода в новое состояние (возможные ходы фигур) и, сравнивая результаты вариантов, отыскивает такой, который характеризуется экстремальным значением оценочной функции (для данной функции имеется в виду максимальное значение). Другими словами, ищется такой ход, который дает наибольший материальный выигрыш.
В то же время для программы игры в «Пятнашки» возможные варианты оценочной функции некоторого состояния должны включать, во-первых, количество фишек, которые стоят не на своих местах, а во-вторых, сумму расстояний по Евклиду от текущего положения каждой фишки до предназначенного ей целевого. При построении алгоритма на основании такой функции, выбирается ветвь, обеспечивающая минимальное значение функции.
Словесное описание алгоритма восхождения на гору можно сформулировать следующим образом:
Шаг1. Находясь в данной точке пространства состояний, применить правила порождения нового множества возможных решений, например множества ходов фигур, допустимых в данной позиции.
Шаг2. Если одно из новых состояний является решением проблемы, прекратить процесс. В противном случае перейти в то состояние, которое характеризуется экстремальным значением оценочной функции. Вернуться к шагу 1.
Но применение этого подхода наталкивается на хорошо известные трудности. Главная из них — как сформулировать оценочную функцию, которая адекватно бы отражала "качество" текущего состояния. Продолжая наш пример с игрой в шахматы, заметим, что иметь много фигур, больше чем у соперника, отнюдь не значит иметь лучшую позицию, т.е. быть ближе к успеху. Такая простая оценочная функция не учитывает многих особенностей этой игры (а в более широком контексте — особенностей данной предметной области).
Более того, даже если оценочная функция и позволяет адекватно оценить текущую ситуацию, существуют разнообразные ситуации игры, которые сами по себе могут быть источником затруднений. Например, в данном состоянии нет очевидного очередного хода, т.е. оказывается, что все возможные ходы одинаково хороши (или плохи). Это не что иное, как выход на "плато" в нашем восхождении, когда ни один из возможных путей не влечет за собой подъем. Другой возможный источник затруднений — наличие локальных экстремумов, из которых возможен только спуск, т.е. "ухудшение" состояния. Например, вариант взять ферзя соперника и после этого проиграть партию.
Таким образом, стратегии, основанные на поиске экстремума, оценивают не только текущее состояние поиска, но и его потомков. Для дальнейшего поиска выбирается наилучший потомок, при этом о его братьях и родителях просто забывают. Поиск прекращается, когда достигается состояние, которое лучше, чем любой из его наследников. Это значит, что в локальном экстремуме стратегия поиска останавливается. Этот факт является ее основным недостатком, поэтому такой алгоритм иногда бывает неприемлем для решения задачи. Однако этот алгоритм может быть очень эффективным, если оценивающая функция позволяет избежать локального экстремума и зацикливания алгоритма.
По своей сути такой алгоритм относится к так называемым «жадным» алгоритмам (greedy algorithm). Жадный алгоритм заключается в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным. Например, рассмотренный вариант алгоритма поиска в глубину, в котором номиналы марок были предварительно отсортированы по убыванию, может быть отнесён к жадным алгоритмам. В данном алгоритме в качестве оценочной функции используется накопленная сумма, и на каждом шаге алгоритма выбирается ветвь (максимальный возможный номинал), обеспечивающая максимум накопленной суммы.
Данный алгоритм может быть ускорен путём замены порождающей операции на вычисление остатка от деления имеющейся суммы на номинал (рисунок 8). В таком виде данная задача и приведённый алгоритм известны, как классическая задача программирования, задача «о размене монет».
1.10 |
|
|
1 |
0.10 |
|
|
2 |
0 |
|
Рисунок 8 − Фрагмент пространства состояний задачи определения последовательности почтовых марок заданной общей стоимости 1 грн. 10 коп из марок с номиналами 5, 30 и 50 коп
Результатом работы данного алгоритма снова станет комбинация 2*0.50+2*0.05=1.10 (грн) и соответствующая ей последовательность (0.50, 0.50, 0.05, 0.05). Теперь она достигается за 2 шага. Но эта комбинация не является последовательностью минимальной длины.
Лучшими свойствами обладает другая форма эвристического поиска, которая также относится к жадным алгоритмам и получила наименование сначала наилучший (best-first search). Так же, как и в варианте восхождения на гору, в нашем распоряжении имеется оценочная функция, с помощью которой можно сравнивать состояния в пространстве состояний. Основное же отличие нового метода от ранее рассмотренного состоит в том, что сравниваются не только те состояния, в которые возможен переход из текущего, но и все возможные потомки. Это даёт возможность использования приоритетной очереди для восстановления алгоритма из точки локального экстремума.
Такой алгоритм требует значительно больших вычислительных ресурсов, т.к. необходимо хранить ранее сделанные оценки состояний и постоянно их обновлять. Но зато данный алгоритм позволяет принимать во внимание не только ближайшие состояния, т.е. локальную обстановку, а "окинуть взглядом" как можно больший участок пространства состояний и, в случае необходимости, вернуться назад и выбрать другой путь.
Существует хорошо известный алгоритм поиска, который относится к группе сначала наилучший, получивший наименование алгоритм А. Основная идея алгоритма состоит в использовании для каждого узла n на графе пространства состояний оценочной функции вида:
f(n) = g(n) + h(n).
Здесь g(n) соответствует расстоянию на графе от узла n до начального состояния, a h(n) —оценка расстояния от n до узла, представляющего конечное (целевое) состояние. Чем меньше значение оценочной функции f(n), тем "лучше", т.е. узел n лежит на более коротком пути от исходного состояния к целевому. Идея алгоритма состоит в том, чтобы с помощью f(n) отыскать кратчайший путь на графе от исходного состояния к целевому.
На практике дать фактическую оценку действительного расстояния до целевого состояния достаточно сложно, но показано, что если h(n) — нижняя оценка расстояния до целевого состояния, т.е. h(n) никогда не дает завышенной оценки расстояния, то алгоритм А всегда отыщет оптимальный путь до цели при помощи оценочной функции f(n). Алгоритм, обладающий таким свойством, называется разрешимым. Разрешимый алгоритм А называют алгоритм А*.
Аналитически получить и затем вычислить значение такой оценки h(n) бывает достаточно сложно, но часто можно показать, что выбранная эвристика ограничена сверху фактической стоимостью кратчайшего пути к целевой вершине. Например, для игры «Пятнашки» число фишек, расположенных не на месте, меньше или равно числу шагов, требуемых для их перемещения в целевую позицию.
В качестве примера определим оценочную функцию h(n) для сформулированной задачи определения последовательности почтовых марок заданной общей стоимости. Использовать в качестве оценочной функции только остаток стоимости почтового отправления недостаточно, т.к. в каждой из ветвей дерева состояний данная функция будет монотонно убывать. При этом будет возрастать накопленная сумму номиналов использованной марочной продукции. Исходя из сказанного выше, будем формировать оценочную функцию так, чтобы на каждом этапе поиска она учитывала не только остаток стоимости почтового отправления, но и накопленную сумму использованных номиналов.
Для этого каждое состояние на графе будем представлять в метрическом пространстве в виде точки с координатами n(x,y), где x− значение остатка, y − накопленное значение. Тогда оценочная функция будет содержать расстояние между узлом-родителем и узлом-потомком. В данной работе выбор оценочной функции осуществлялся эмпирическим путём, рассматривались: метрика Эвклида, метрика Манхеттена, метрика Чебышева, метрика Камберра, косинусное расстояние и коэффициент корреляции.
В результате были сформированы две оценочные функции:
нецентрированный коэффициент корреляции Пирсона,

![]()
разность между остатком
 и косинусным расстоянием
и косинусным расстоянием
 ,
,
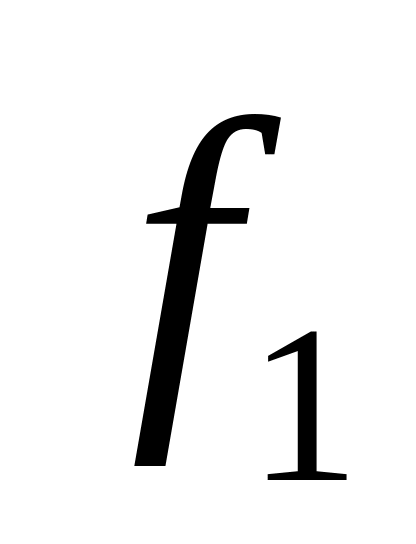
![]() ,
,
 .
.
Для рассмотренного примера (общая стоимость 1 грн. 10 коп и марки номиналами 5, 30 и 50 коп) фрагмент графа пространства состояний при решении алгоритмом А* с оценочной функцией приведён на рис. 9. Каждая вершина графа при этом обозначается кортежем из трёх элементов (x,y,g(n)). Как и прежде, поиск осуществляется от цели, состояния (1.10,0,0). Решением является вершина с x=0 и y=1.10. Выбор ветви графа осуществляется из условия min(f1).
(1.10,0,0) f1=∞ |
|||||||||
|
1 |
|
2 |
3 |
|
||||
(0.6,0.5,1) f1=1.368 |
(0.8,0.3,1) f1=1,736 |
(1.05,0.05,1) f1=2.049 |
|||||||
4 |
|
5 |
. 6 |
|
|||||
(0.1,1,2) f1=2,29 |
(0.3,0.8,2) f1=2,17 |
(0.55,0.55,2) f1=2,45 |
|||||||
|
7 |
||||||||
(0,1.10,3) |
|||||||||
Рисунок 9 − Фрагмент пространства состояний задачи определения последовательности почтовых марок заданной общей стоимости 1 грн. 10 коп из марок с номиналами 5, 30 и 50 коп
Из приведённого фрагмента видно, что найдена комбинация минимальной длины 0.50+2*0.30=1.10 (грн) и на это затрачено 7 шагов, что в 2 раза меньше, чем при слепом поиске в ширину.
Результаты использования различных оценочных функций приведены для набора марок с номиналами 5, 30 и 50 коп в табл.1.
Таблица 1 – Результаты использования различных оценочных функций
Стоимость почтового отправления, грн |
0.6 |
0.9 |
0.95 |
1.10 |
|
Количество шагов при использовании |
|
4 |
9 |
12 |
7 |
|
5 |
10 |
21 |
11 |
|
Для записи псевдокода данного алгоритма воспользуемся следующими обозначениями:
start — узел начального состояния;
goal — узел целевого состояния;
OPEN — список, который содержит, выбранные, но необработанные узлы;
CLOSED — список, который содержит обработанные узлы.
Таким образом, псевдокод алгоритма А имеет вид (листинг 2).
Листинг 2 – Листинг алгоритма А
function best_first_search;
begin
//инициализаиия
OPEN := [Start];
CLOSED := [];
while open ≠ [] do
//оставшиеся состояния
begin
удалить первое состояние X из списка open;
if (X=goal)
return (путь от Start к X)
else
begin
сгенерировать потомок X;
for каждого потомка X do
case
begin
потомок не содержится в списке open или closed:
begin
присвоить потомку эвристическое значение;
добавить потомок в список open;
end;
потомок уже содержится в списке OPEN:
if (потомок был достигнут по кратчайшему пути)
записать это состояние в список OPEN;
потомок уже содержится в списке CLOSED:
if (потомок был достигнут по кратчайшему пути)
begin
удалить состояние из списка CLOSED;
добавить потомок в список OPEN;
end;
end; //case
поместить X в список CLOSED;
переупорядочить состояния в списке OPEN в соответствии с эвристикой (лучшие слева);
end; //else
end; // while
return FAIL; //спиcок OPEN пуст
end.
2 ДОВІДКОВІ ДАНІ
Таблиця 2.1 – Випуск марочної продукції за 2010-2013 р.р.
№ номіналу |
Номінал, грн/ Літера |
Рік випуску 2010 |
Рік випуску 2011 |
Рік випуску 2012 |
Рік випуску 2013 |
Стандартні поштові марки |
|||||
1 |
0,05 |
|
|
х |
|
2 |
0,20 |
|
|
х |
|
3 |
0,30 |
|
|
х |
|
4 |
0,40 |
|
|
х |
|
5 |
0,50 |
|
|
х |
|
6 |
0,70 |
|
|
х |
|
7 |
1,00 |
х |
х |
|
|
8 |
1,30 |
х |
|
|
|
9 |
1,50 |
х |
х |
|
|
10 |
1,80 |
|
х |
|
|
11 |
1,90 |
|
х |
|
|
12 |
2,00 |
х |
х |
х |
|
13 |
2,20 |
х |
х |
|
|
14 |
2,50 |
|
|
х |
|
15 |
3,00 |
|
|
х |
|
16 |
3,30 |
х |
|
х |
|
17 |
4,00 |
|
|
х |
|
18 |
4,30 |
|
х |
х |
|
19 |
4,80 |
|
|
х |
|
20 |
5,00 |
|
|
х |
|
21 |
5,30 |
|
|
х |
|
22 |
5,40 |
|
|
х |
|
23 |
6,00 |
|
х |
|
|
24 |
7,00 |
|
х |
|
|
25 |
7,70 |
|
х |
|
|
26 |
8,00 |
|
|
х |
|
27 |
10,00 |
|
|
х |
|
28 |
12,00 |
|
|
х |
|
29 |
13,80 |
|
|
х |
|
Літерні поштові марки |
|||||
|
Ж |
|
|
х |
|
|
L |
|
|
х |
|
|
N |
|
|
|
х |
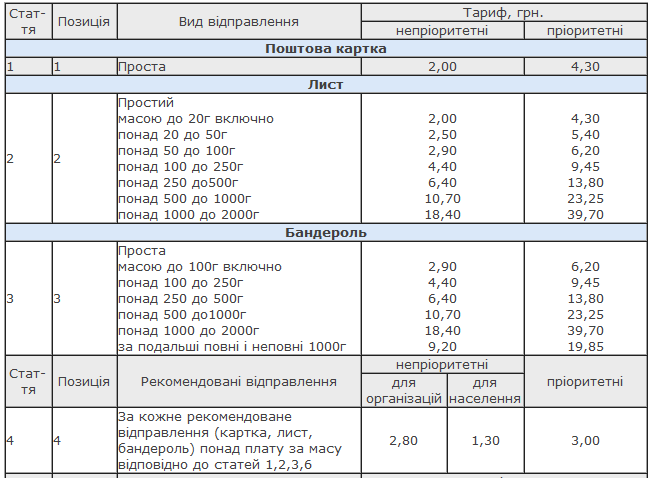
Таблиця 2.2 – Тарифи УДППЗ «Укрпошта» на послуги пересилки письмової кореспонденції
Таблиця 2.3 – Тарифи УДППЗ «Укрпошта» на послуги пересилки письмової кореспонденції з оголошеною цінністю
Стаття |
Пози-ція |
Види послуг і відправлень |
Тариф, грн. |
||
1 |
2 |
3 |
4 |
5 |
|
Поштові відправлення з оголошеною цінністю |
|||||
2 |
2 |
Лист, бандероль
масою до 100г включно понад 100 до 250г понад 250 до 500г понад 500 до1000г понад 1000 до 2000г понад 2000 до 3000г |
непріоритетні |
пріоритетні |
|
5,30 6,40 7,50 10,10 14,60 22,60 |
6,20 9,45 13,80 23,25 39,70 59,55 |
||||
Оголошена цінність поштових відправлень |
|||||
За оголошену цінність поштового відправлення від суми оголошеної цінності в гривнях понад плату за масу ст.1,2,3,4, % до 1000 грн. включно понад 1000 грн. але не менше ніж 2,50 грн. |
1,00 0,5 |
||||
Таблиця 2.4 – Тарифи УДППЗ «Укрпошта» на послуги повідомлення про вручення та супутні послуги поштового зв’язку
Повідомлення про вручення |
||
1 |
Повідомлення про вручення, грн |
3,50 |
Супутні послуги, пов’язані з наданням послуг поштового зв’язку |
||
2 |
Зберігання листа (бандеролі) з оголошеною цінністю, дрібного пакета, міжнародного поштового відправлення з оголошеною цінністю – масою понад 500 грамів, а також мішка “М”, згрупованих поштових відправлень з позначкою “Консигнація”, посилки, прямого контейнера, у тому числі за заявою адресата (одержувача), понад п’яти робочих днів об’єкта поштового зв’язку після надходження (за кожну добу), але не більше ніж 15,50 грн. При цьому день видачі поштового відправлення не враховується |
3,10 |
3 |
Написання адреси на поштовому відправленні; заповнення відповідного бланку, за одиницю |
1,50 |
4 |
Формування списку ф.103 на згруповані відправлення, за кожний список |
6,60 |
5 |
Упакування поштового відправлення (з урахуванням вартості паперу, шпагату, стрічки тощо), за одне відправлення |
3,00 |
6 |
За письмову заяву (довідку) 5: - для населення - для організацій |
10,00 25,00 |
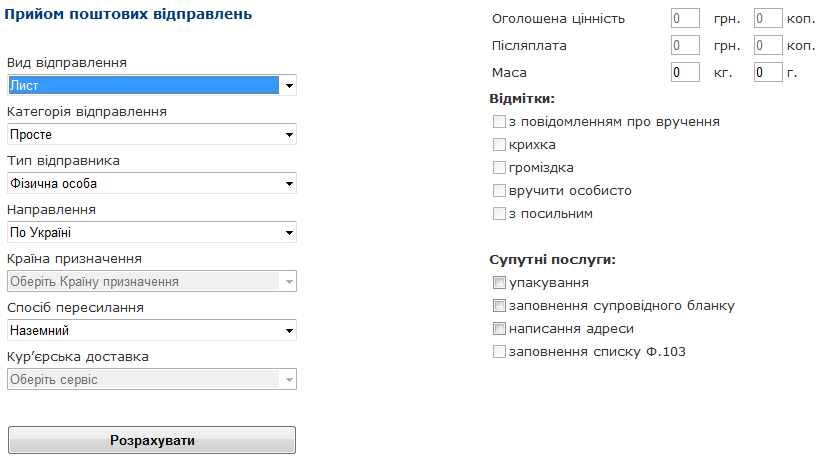
Рисунок 2.1 – Інтерфейс застосування «Калькулятор послуг»
3 ЗАВДАННЯ
Згідно заданого варіанту:
1. Розрахувати обчислювальну складність методу повного «грубого» перебору;
2. Навести фрагмент графу простору станів для використання алгоритму А із оціночною функцією ;
3. Навести фрагмент графу простору станів для використання алгоритму А із оціночною функцією ;
4. Розробити мовленевий опис алгоритму застосування;
5. Розробити застосування із дотриманням вимог.
Вимоги до застосування:
написання на мові програмування С++;
наявність графічного інтерфейсу користувача.
4 ВИХІДНІ ДАНІ ТА ВАРІАНТИ ЗАВДАННЯ
№ вар. |
Вартість відпр. |
Застосування |
1 |
2.00 |
Калькулятор послуг |
2 |
2.50 |
Калькулятор марок |
3 |
2.90 |
Калькулятор послуг |
4 |
4.40 |
Калькулятор марок |
5 |
6.40 |
Калькулятор послуг |
6 |
10.70 |
Калькулятор марок |
7 |
18.40 |
Калькулятор послуг |
8 |
4.30 |
Калькулятор марок |
9 |
6.20 |
Калькулятор послуг |
10 |
9.45 |
Калькулятор марок |
11 |
13.80 |
Калькулятор послуг |
12 |
23.25 |
Калькулятор марок |
13 |
39.70 |
Калькулятор послуг |
14 |
5.30 |
Калькулятор марок |
15 |
7.50 |
Калькулятор послуг |
16 |
10.10 |
Калькулятор марок |
17 |
14.60 |
Калькулятор послуг |
18 |
22.60 |
Калькулятор марок |
19 |
8.20 |
Калькулятор послуг |
20 |
12.45 |
Калькулятор марок |
21 |
16.80 |
Калькулятор послуг |
22 |
4.20 |
Калькулятор марок |
23 |
5.70 |
Калькулятор послуг |
24 |
7.70 |
Калькулятор марок |
25 |
12.00 |
Калькулятор послуг |
26 |
7.20 |
Калькулятор марок |
27 |
9.20 |
Калькулятор послуг |
28 |
19.20 |
Калькулятор марок |
29 |
8.90 |
Калькулятор послуг |
30 |
10.00 |
Калькулятор марок |
№ Номинала № вар. |
|
||||||
1 |
1 |
6 |
2 |
29 |
27 |
26 |
22 |
2 |
5 |
3 |
22 |
16 |
26 |
14 |
2 |
3 |
2 |
25 |
10 |
11 |
4 |
22 |
1 |
4 |
7 |
1 |
9 |
2 |
8 |
2 |
28 |
5 |
7 |
1 |
10 |
6 |
3 |
23 |
20 |
6 |
4 |
2 |
14 |
10 |
17 |
16 |
3 |
7 |
20 |
22 |
2 |
3 |
29 |
13 |
6 |
8 |
4 |
5 |
10 |
14 |
15 |
18 |
7 |
9 |
12 |
1 |
19 |
26 |
6 |
23 |
3 |
10 |
13 |
8 |
29 |
15 |
5 |
20 |
7 |
11 |
2 |
4 |
14 |
12 |
8 |
6 |
20 |
12 |
20 |
6 |
25 |
3 |
10 |
25 |
1 |
13 |
11 |
13 |
5 |
25 |
2 |
21 |
5 |
14 |
21 |
6 |
7 |
10 |
4 |
26 |
29 |
15 |
13 |
4 |
14 |
18 |
24 |
25 |
7 |
16 |
15 |
12 |
4 |
9 |
10 |
5 |
15 |
17 |
10 |
29 |
20 |
6 |
8 |
5 |
3 |
18 |
2 |
28 |
18 |
17 |
7 |
21 |
23 |
19 |
7 |
29 |
6 |
4 |
24 |
25 |
8 |
20 |
29 |
5 |
3 |
1 |
6 |
18 |
26 |
21 |
11 |
17 |
13 |
24 |
9 |
7 |
6 |
22 |
20 |
27 |
8 |
16 |
21 |
7 |
3 |
23 |
7 |
8 |
1 |
17 |
25 |
16 |
17 |
24 |
7 |
23 |
24 |
11 |
16 |
8 |
14 |
25 |
24 |
29 |
11 |
1 |
22 |
20 |
28 |
26 |
4 |
8 |
10 |
15 |
7 |
3 |
23 |
27 |
8 |
25 |
24 |
20 |
4 |
1 |
3 |
28 |
1 |
3 |
6 |
15 |
11 |
8 |
2 |
29 |
5 |
16 |
8 |
12 |
4 |
10 |
11 |
30 |
16 |
20 |
28 |
3 |
26 |
5 |
7 |
