
1.5 Поиск в глубину
Для любого данного узла N алгоритм поиска в глубину строит потомок этого узла, т.е. формирует состояние, которое образуется в результате применения операторов к узлу N. Если решение не найдено, алгоритм переходит к формированию узла, ближайшего к N, на том же уровне графа ("соседу" N), т.е. формирует состояние, которое образуется в результате применения оператора к узлу-родителю N. Иначе говоря, в алгоритме поиска в глубину просматриваются все состояния на одном пути, то есть исследуется некий узел, оцениваются все его потомки и потомки его потомков, а затем происходит возврат назад на один уровень и исследуется любая из вершин-братьев.
Различия в организации прямого и обратного поиска в пространстве состояний с помощью алгоритмов поиска в глубину и ширину приведены на рис. 3.
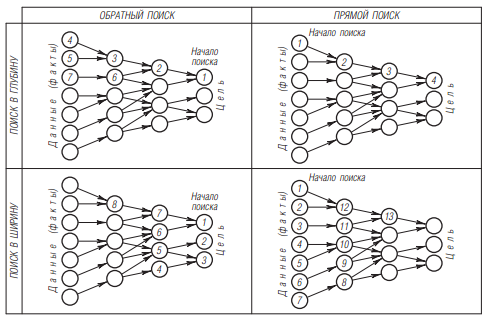
Рисунок 3 – Методы организации поиска в системах искусственного интеллекта
На рисунке числа на дугах графа указывают номер шага, на котором формируется тот узел (состояние), для которого эта дуга является входящей. Конечно, этот номер еще зависит и от того, в каком порядке используются операторы из имеющегося множества.
Для игры в Scrabble граф пространства состояний при использовании алгоритма поиска в глубину приведён на рисунке 4.
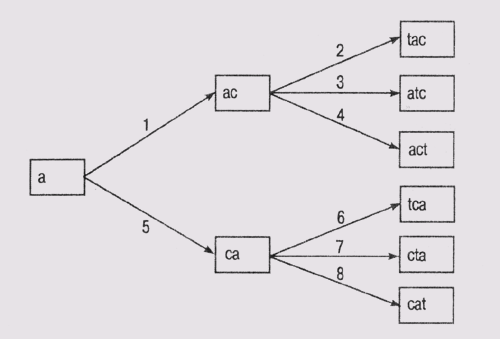
Рисунок 4 − Граф пространства состояний при использовании алгоритма поиска в глубину
В представленном примере сначала применяется оператор, добавляющий очередную букву в конец последовательности, затем оператор, добавляющий букву на предпоследнюю позицию, и т.д., а последним применяется оператор, добавляющий букву на первое место. Но ведь можно использовать и обратный порядок применения операторов.
Отметим, что данный алгоритм алгоритма завершит работу (найдет конечное состояние) после формирования узла "act", а не "cat". Тем не менее, алгоритму поиска в глубину придется для этого сформировать и проанализировать пять состояний.
Рассмотрим решение задачи определения последовательности почтовых марок заданной общей стоимости с использованием алгоритма поиска в глубину. Предположим, что стоимость почтового отправления составляет 1 грн. 10 коп. В распоряжении оператора отделения связи находятся марки с номиналами: 5, 30 и 50 коп, а также 2 грн. Поиск ведётся в обратном направлении (от цели): цель - набрать с помощью имеющихся номиналов сумму 1 грн. 10 коп., поэтому в качестве цели используем состояние 1.10. В качестве операции порождения нового состояния используется вычитание номинала марки. Решением является состояние, в котором результат порождающей процедуры, т.е. вычитания очередного номинала, равен 0. Для нахождения решения осуществляются: сначала порождение очередной вершины, затем проверка на равенство 0. Фрагмент пространства состояний этой задачи приведён на рис. 5.
1.10 |
|||||||||
1 |
|
|
|||||||
1.05 |
… |
0.60 |
|||||||
|
2 |
... |
|
|
|
|
|
|
|
… |
|
|
|
… |
0.10 |
||||
21 |
|
|
|
||||||
0.05 |
|||||||||
|
22 |
||||||||
0 |
|||||||||
Рисунок 5 − Фрагмент пространства состояний задачи определения последовательности почтовых марок заданной общей стоимости 1 грн. 10 коп из марок с номиналами 5, 30 и 50 коп
На приведённом фрагменте можно увидеть только 2 пути решения задачи:
комбинация из 22-х марок достоинством 5 коп;
комбинация 2-х марок по 50 коп и 2-х марок по 5 коп.
На данном графе не приведены запрещённые состояния решения задачи, а именно состояния, образованные дугами вычитания номинала 2 грн.
Заметим, что длины путей на графе существенно отличаются: 1-ый путь содержит 21 промежуточную вершину, а 2й только 3.
Результатом поиска в глубину станет комбинация из 22-х марок достоинством 5 коп. Подобную реализацию поиска, часто называют слепым поиском, т.к. выбор пути решения производится вслепую.
Полученный результат можно существенно улучшить, если найти правило для выбора пути решения. Очевидно, что для реализации такого правила можно отсортировать номиналы марок по убыванию. Тогда первой операцией над исходным узлом станет вычитание не наименьшего, а наибольшего возможного номинала (в данном примере 50 коп) и поиск решения будет осуществлён по второму пути.
Итого, поиск в глубину позволил сформировать последовательность номиналов за 4 шага.
Очевидным также является тот факт, что найденная комбинация 2*0.50+2*0.05=1.10 (грн) и соответствующая ей последовательность (0.50, 0.50, 0.05, 0.05) не является последовательностью минимальной длины.
Кратчайшей последовательностью в данном примере является, например, последовательность из трёх номиналов (0.50, 0.30, 0.30): 0.50+2*0.30=1.10 (грн).
Рассмотрим псевдокод алгоритма поиска в глубину (листинг 1). Он записан с помощью функциональной нотации, которая подчеркивает его рекурсивную структуру. Таким образом, dfs представляет собой функцию трех аргументов: goal, current и pending:
goal — это объект поиска,
current — текущий узел на графе состояний (в самом начале — узел исходного состояния),
pending — список узлов, претендующих на обработку (в самом начале — пустой).
В дальнейшем используются следующие обозначения:
символ := означает присваивание;
функция expand формирует узлы, следующие за аргументом этой функции;
знак + означает слияние двух списков, т.е.
(а b с) + (d e f ) = (а b с d e f);
() означает пустой список;
first и rest — функции, которые возвращают начало и конец списка:
first(a b с) = a
rest(a b c) = (b c).
Листинг 1− Псевдокод алгоритма поиска в глубину
dfs(goal, current, pending)
{
if (current = goal)
then success;
else
{
pending := expand (current)+ pending;
if (pending = ())
then fail;
else
dfs(goal, first(pending), rest( pending));
}
}
1.6 Поиск в ширину
Алгоритм поиска в ширину действует наоборот — сначала формируются все "соседи" узла N, и если решение не найдено, строятся его потомки. Таким образом, в алгоритме поиска в ширину просматриваются последовательно состояния, представленные узлами одного и того же уровня на графе пространства состояний, и лишь потом осуществляется переход к фактам следующего уровня детализации.
Для игры в Scrabble граф пространства состояний при использовании алгоритма поиска в ширину приведён на рисунке 6.
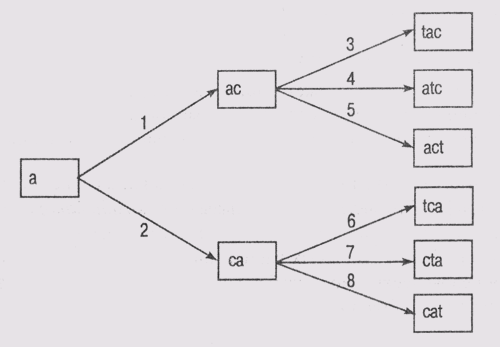
Рисунок 6 − Граф пространства состояний при использовании алгоритма поиска в ширину
Данный алгоритм также завершит работу (найдет конечное состояние) после формирования узла "act", но для этого будут сформированы и проанализированы пять состояний (пять узлов), что больше на 1 узел, чем при поиске в глубину.
Для сформулированной задачи определения последовательности почтовых марок заданной общей стоимости 1 грн. 10 коп из марок с номиналами 5, 30 и 50 коп фрагмент пространства состояний представлен на рис. 7. В данном примере: поиск также осуществляется от цели (вершины 1.10), номиналы марок отсортированы по убыванию, операция порождения состояния – вычитание номинала, решение – состояние 0.
1.10 |
||||||||||||||||||
|
1 |
2 3 |
|
|||||||||||||||
0.60 |
0.80 |
1.05 |
||||||||||||||||
|
4 |
5 6 |
|
|
7 |
8 9 |
|
|
10 |
11 12 |
|
|||||||
0.10 |
0.30 |
0.55 |
0.30 (петля) |
0.5 |
0.75 |
0.55 (петля) |
0,75 (петля) |
1.00 |
||||||||||
|
13 |
14 |
… |
… |
||||||||||||||
0.05 0 |
||||||||||||||||||
Рисунок 7 − Фрагмент пространства состояний задачи определения последовательности почтовых марок заданной общей стоимости 1 грн. 10 коп из марок с номиналами 5, 30 и 50 коп
На данном фрагменте также не приведены запрещённые состояния решения задачи, а именно состояния, результат вычитания в которых будет отрицателен.
В отличие от поиска в глубину, алгоритму поиска в ширину удаётся определить кратчайшую последовательностью номиналов (0.50, 0.30, 0.30), но на это затрачивается 14 шагов.
Сравнивая между собой алгоритмы поиска в глубину и в ширину, отметим, что если решение расположено только в правой нижней вершине графа, то обе эти стратегии гарантируют рассмотрение всех возможных состояний (полный «грубый» перебор).
Тем не менее, свойства этих алгоритмов существенно отличаются. Алгоритм поиска в глубину может найти решение быстрее поиска в ширину, особенно, если при его выполнении используются эвристики для выбора очередной ветви. Но, во-первых, это необязательно будет оптимальное решение, а, во-вторых, если пространство состояний бесконечно, алгоритм поиска в глубину может никогда не закончиться.
Алгоритм поиска в ширину отыскивает решение, путь к которому на графе — кратчайший, если таковое существует. Т.е. кратчайший путь между исходным состоянием и решением. Алгоритмы, обладающие таким свойством, называются разрешимыми (admissible).
Исходя из сказанного выше, выбор стратегии определяется спецификой задачи. Так, поиск в глубину подходит для решения проблемы, где все пути поиска имеют приблизительно одинаковую длину. Поиск в ширину пригоден для задач, где ветви дерева поиска имеют сильно различающуюся длину, и нет четких указаний на то, какой путь быстрее приводит к цели.
В практических задачах, как правило, не применяется только одна из стратегий поиска. Алгоритмы комбинируют обе стратегии, в зависимости от свойств предметной области и среды поиска. Хорошим примером комбинированного алгоритма поиска является использование предельного значения глубины поиска. Предельная глубина позволяет ограничить поиск только заданным числом уровней. Это обеспечивает некоторое подобие развёртывания области поиска в ширину при поиске в глубину.
К сожалению, можно показать, что в наихудшем случае поиск в глубину, в ширину и с заглублением обладают экспоненциальной сложностью, т.е. число узлов растет экспоненциально по мере увеличения числа уровней на графе. Это явление часто называют комбинаторным взрывом и оно представляет очень серьезную проблему при программировании таких задач, например при полном "грубом" переборе всех возможных вариантов. Исследованием вычислительной обозримости (или необозримости) проблем занимается теория сложности. Существуют классы проблем, решение которых требует ресурсов, экспоненциально возрастающих при линейном увеличении размерности задачи. Например, время, необходимое для отыскания пути в лабиринте, экспоненциально увеличивается при увеличении количества разветвлений в лабиринте. Аналогично, время, необходимое для поиска доказательства теоремы исчислением утверждений, растет экспоненциально по отношению к количеству переменных. Такие проблемы являются в общем случае необозримыми и называются NP-hard.
Проблемы, время решения которых связано с размерностью задачи полиномиальной функции, считаются обозримыми. Например, проверка заданного маршрута в лабиринте или проверка правильности доказательства некоторой теоремы — обозримые проблемы. Но можно показать, что, к сожалению, большинство проблем, которые интересуют нас в области искусственного интеллекта, относятся к классу NP-hard. Поэтому такое важное значение придается использованию эвристических методов при их решении.
