ІНДИВІДУАЛЬНЕ ЗАВДАННЯ №1

(Комплексне завданння)

з дисципліни «Основи інформатизації»

для студентів спеціальності ПЗ

1 Ключові положення

Почтовая марка — специальный знак почтовой оплаты, обладающий определённой номинальной стоимостью. Для осуществления оплаты за пересылку письменной корреспонденции, почтовое отправление должно быть франкировано последовательностью почтовых марок с соответствующей общей стоимостью. Сегодня распространенным явлением является франкировка вручную почтовых отправлений непосредственно клиентом или оператором отделения связи. Поэтому проблема разработки автоматического метода определения оптимальных по длине последовательностей почтовых марок с заданной общей стоимостью является актуальной.

Очевидно, что данная проблема, в существенной степени, является следствием недостатков применяемых методов тарифообразования и создания оптимальных наборов марочных номиналов.

Однако даже при удачно сформированной тарифной сетке и оптимальном выборе номиналов марочной продукции, на практике не избежать ситуации, когда в отделении связи часть номиналов отсутствует и в наличии имеется только ограниченный набор марочной продукции. К тому же не следует исключать влияние человеческого фактора, который часто становится причиной ошибок сотрудника-оператора при подборе комбинаций марок.

Данные ошибки и, в частности, выбор при франкировке последовательности марок большей длины ведёт к:

- неэффективному использованию марочной продукции и необоснованным затратам на её изготовление;

- дополнительным трудозатратам оператора;

- неэффективному использованию рабочего времени оператора;

- снижению качества обслуживания.

Исходя из всего вышесказанного, целью данной работы является разработка автоматического метода определения оптимальных по длине последовательностей почтовых марок заданной общей стоимости с использованием методов искусственного интеллекта.

1.1 Поиск в пространстве состояний. Графовое представление задачи в пространстве состояний

Фундаментальная идея, именуемая поиск в пространстве состояний (state space search), достаточно проста и основывается на том факте, что процесс решения множества проблем может быть разделён на этапы:

• исходное состояние проблемы, например исходное состояние головоломки;

• тест завершения — проверка, достигнуто ли требуемое конечное состояние или найдено решение проблемы (примером может послужить правило определения, собрана ли головоломка);

• множество операций, которые можно использовать для изменения текущего состояния проблемы, например шаги или перемещения фигур при сборке головоломки.

Один из способов представления такого концептуального пространства состояний — граф, в котором состояниям соответствуют узлы, а операциям — дуги.

Во многих задачах искусственного интеллекта часто возникает необходимость наглядного представления отношений между какими-либо объектами. Для таких отношений существует естественная модель — это ориентированный и неориентированный графы.

Ориентированный граф (или сокращено орграф) G=(N, E) состоит из множества вершин N и множества дуг E. Вершины также называют узлами, а дуги — ориентированными ребрами. Множество вершин N₁, N₂,…,N_n не обязано быть конечным. Дуга представляется в виде упорядоченной пары вершин (N₃, N₄), где N₃ называется начатом, а N₄ —концом дуги. Дугу (N₃, N₄) часто записывают как N₃ → N₄. Говорят также, что дуга N₃ → N₄ ведет от вершины N₃, к вершине N₄. а вершина N₄ смежна с вершиной N₃.

Если направленная дуга соединяет вершины N_j и N_k, то N_j называется родителем N_k, a N_k — потомком N_j. Если граф содержит также дугу (N_j, N_i), то N_k и N_i, называются вершинами-братьями. Корневой граф имеет единственную вершину N_s, в которую не входит ни одна дуга. Таким образом, корень графа не имеет родителей.

Концевая вершина —это вершина, которая не имеет потомков.

Упорядоченная последовательность вершин [N₁, N₂,..., N_n], где каждая пара является дугой, называется путем длины п-1 на графе. Одну вершину можно считать путем длины 0 от вершины к этой же вершине. Путь называется простым, если все вершины на нем, за исключением может быть первой и последней, различны. Цикл — это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине.

Если путь включает некоторую вершину более одного раза, то говорят, что путь содержит петлю.

Если к вершинам и дугам орграфа присоединить какую-либо информацию, то получим помеченный орграф, при этом каждая дуга и/или каждая вершина имеет соответствующие метки. Меткой может быть имя, вес или стоимость (дуги), или значение данных какого-либо заданного типа.

В корневом графе вершина называется предком всех вершин, расположенных после неё, и в то же время потомком всех вершин, расположенных на пути к ней.

Неориентированный граф G = (N, E) состоит из конечного множества вершин N и множества ребер E. В отличие от ориентированного графа каждое ребро здесь соответствует неупорядоченной паре вершин: если (N₃, N₄) — нeopиентированное ребро, то (N₃, N₄)= (N₄, N₃). Неориентированный граф будем называть просто графом.

Дерево с базовым типом Т в программировании определяется как: 1) пустое дерево; либо 2) некоторая вершина типа Т с конечным числом связанных с ней отдельных деревьев с базовым типом Т, называемых поддеревьями. В системах искусственного интеллекта понятие дерева часто связывают с понятием графа.

Рассматривая дерево как неориентированный граф, можно сказать, что в нем существует единственный путь между любыми двумя вершинами (т. е. пути в дереве не содержат циклов). Каждая вершина в корневом дереве имеет единственного родителя. Две вершины называются связными, если существует путь, содержащий эти вершины.

Множество состояний, достижимых из данного начального состояния, полезно представлять в виде графа, вершины которого соответствуют этим состояниям. Вершины такого графа связаны между собой дугами, которые описывают переходы между состояниями. Эти переходы соответствуют логическим заключениям или допустимым операциям в ходе решения.

Поиск в пространстве состояний характеризует решение задачи как процесс нахождения пути решения (цепочки, ведущей к решению задачи) от исходного состояния к целевому. Пространство состояний можно представить четверкой [N, A, S, GD] со следующими обозначениями: N —множество вершин графа или состояний в процессе решения задачи; A — множество дуг между вершинами, соответствующих шагам в процессе решения задачи; S — непустое множество начальных состояний задачи; GD— непустое множество, состоящее из целевых состояний. Эти состояния описываются одним из следующих способов:

1) измеряемыми свойствами состояний, встречающихся в процессе поиска:

2) свойствами путей, возникающих в процессе поиска, например, стоимостью перемещения по дугам пути.

Допустимый путь — это путь из вершины множества S в вершину из множества GD. Путь является целью поиска. Он начинается от исходного состояния и продолжается до тех пор, пока не будет достигнуто условие цели.

Задача алгоритма поиска решения состоит в нахождении допустимого пути в пространстве состояний. Состояния иногда могут быть достигнуты разными путями, поэтому важно выбирать оптимальный путь.

Графовое представление задачи в пространстве состояний имеет ряд преимуществ:

• интуитивно легко понять нетривиальные высказывания;

• учитывается стоимость применения оператора 0^(k), она помечается на каждой дуге графа;

• каждый последовательный шаг можно определять при помощи функции сравнения целевого и текущего состояний.

Приведем фрагмент пространства состояний для игры «крестики-нолики» (рис. 1). Корневая вершина этого графа будет соответствовать пустой игровой доске, указывающей на начало игры. Каждый следующий узел графа будет представлять состояние игровой доски, возникающее в процессе игры в результате допустимых ходов, а дуги между ними — связи между вершинами.

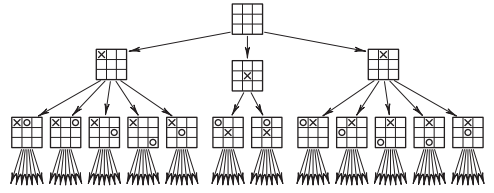
Рисунок 1 – Фрагмент пространства состояний игры «крестики-нолики»

В качестве другого примера рассмотрим задачу построения слова из некоторого множества букв, как в игре Scrabble. Задавшись набором операций установки букв, можно сформировать пространство состояний.

Предположим, что множество доступных букв включает Т, С и А. На каждом уровне графа мы будем добавлять по одной определенной букве. Каждая ветвь, исходящая из узла, соответствует установке буквы в определенную позицию в последовательности, а эта последовательность должна образовать осмысленное слово (рис. 2). Если это произошло, то головоломка считается собранной (например, если образовалась комбинация "act" или "cat").

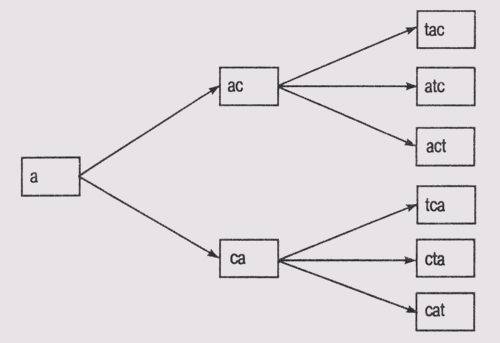
Рисунок 2 − Дерево пространства состояний головоломки Scrabble с буквами Т, С и А

Пространство состояний, приведённое на рис. 2, обладает двумя интересными свойствами, которые присущи далеко не всем пространствам состояний:

• оно конечно, поскольку существует только n! способов расставить n букв;

• оно не содержит повторяющихся узлов, что может привести к образованию петель на графе.