§3. Преобразование трехмерных аномалий в двухмерные

В тех случаях, когда формулы для двухмерных тел нельзя применить к трехмерным, специальным приемом сводят трехмерную аномалию к двухмерной. Рассмотрим этот прием на примере анома­лии U_z, поскольку для U_xz и U_zz требования к двухмерности значи­тельно слабее. В точке с координатами (0, у, 0) имеем

U_z(o, y, 0) = kσ .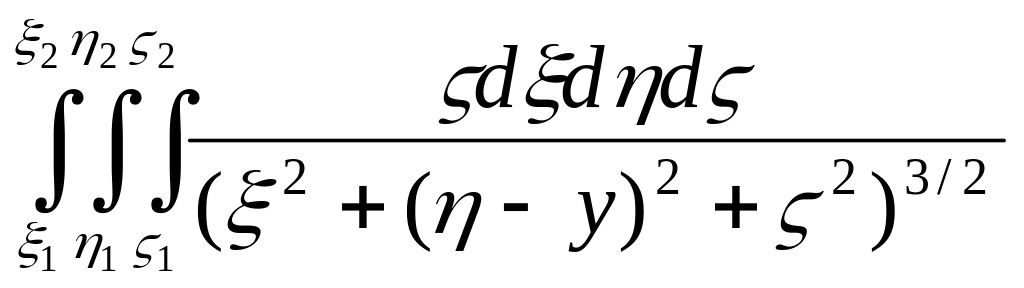

Умножаем обе части этого выражения на dy и интегрируем их по у в пределах ±∞:

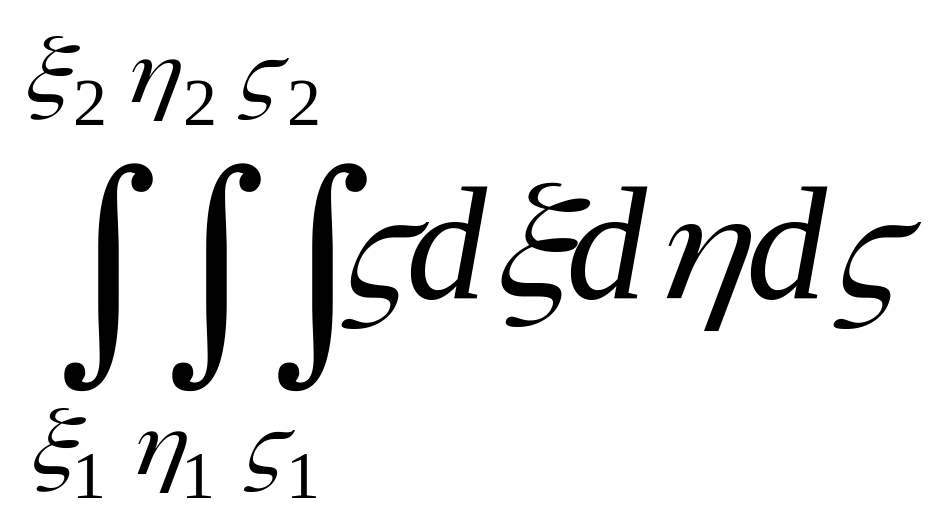= k σ . (38)

Учитывая выражение (19) и полагая

σ = σ_α,

получаем

dy = 2kσ_α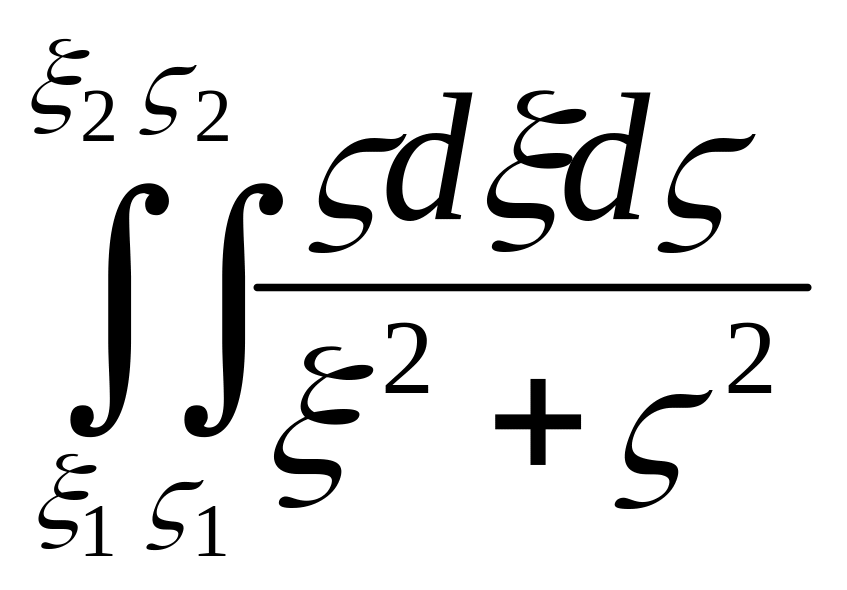 . (39)

Правая часть этого выражения представляет собой формулу U_z двухмерного тела. Отсюда следует, что трехмерную задачу можно свести к двухмерной, если вдоль профиля, расположенного вкрест

простирания тела, рассматривать не кривую U_z, а кривую dy. По такой кривой получаем истинные геометрические параметры тела, но не плотность σ.

При использовании этого приема на практике приходится огра­ничиваться интегрированием в конечных пределах, поскольку ано­малия известна в ограниченной области и на периферии может быть искажена влиянием соседних аномалий. Оценим относительную погрешность ε, возникающую из зa ограничения пределов интегри­рования.

Положим, что тело, создающее гравитационную аномалию, пред­ставляет собой шар. Помещая начало координат над центром шара, имеем

ε = 1 - 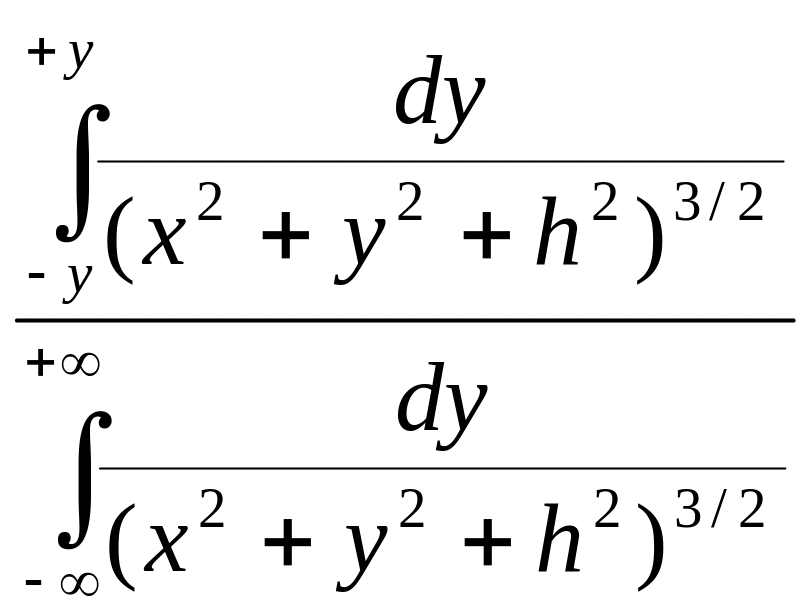= 1 - б

где

p² = x² + h².

Принимая h/y < 1, в центре аномалии (0 = 0; р = h) получаем

ε = 1 – (1+( )²)^-1/2 = ( )² + ( )⁴. (40)

Для различных отношений рассчитана величина ε:

	0.5	0.3	0.2	0.1
ε	0.15	0.04	0.02	0.01

Отсюда видим, что уже при h/y = 0,2 конечность пределов интегрирования мало сказывается на окончательном результате.

Уменьшить погрешность интерпретации, связанную с заменой трехмерной задачи двухмерной, можно также трансформацией аномалий силы тяжести в такие производные, для которых требования к двухмерности невелики. Такого же результата можно добиться и соответствующим расположением интерпретационных профилей относительно аномального тела.

§4. Определение рельефа контактной поверхности

Контактной поверхностью называется поверхность раздела двух сред с различными плотностями. Определение рельефа контактной поверхности по наблюдениям силы тяжести имеет большое значение в практике гравиметрических работ. Контактной поверхности могут быть уподоблены рельеф кристаллического фундамента, отдельные складчатые структуры и т. д.

Пусть MN - горизонтальная поверхность, на которой проведены наблюдения силы тяжести. Ниже ее располагается пов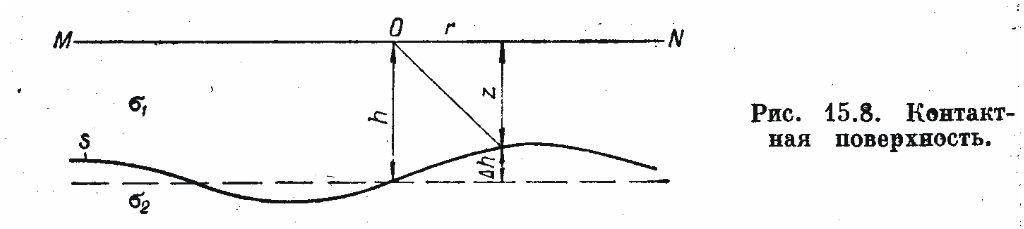 ерхность S произвольной формы, разделяющая две толщи пород с различной плотностью. Пусть σ₁ - плотность пород верхней толщи, σ₂ - плотность пород нижней толщи, избыточная плотность σ = σ₂ - σ₁. Очевидно, что при σ >0 положительным формам рельефа границы S соответствуют положительные приращения ано­малии U_z, и наоборот, отрицательным формам границы S соответ­ствуют отрицательные приращения аномалии.

Полагая начало координат в точке наблюдения О, из формулы. U_z(0, 0, 0) = kσ имеет выражение аномалии U_z от контактной поверхности:

U_z(0, 0, 0) = kσ , (41)

где r и α - полярные координаты точки наблюдения; z - глубина контактной поверхности в этой точке; h - средняя глубина контактной поверхности.

Поскольку глубина ζ, является функцией координат г и α, опре­деление ее связано с решением уравнения, в котором эта функция находится под знаком интеграла. Относительно функции z(r, α) выражение (41) является нелинейным интегральным уравнением, алгоритмов для решения которых не разработано. Поэтому точное решение задачи о контактной поверхности невозможно. Необходимо упростить математическую постановку задачи, чтобы получить приближенное решение.

Проинтегрировав выражение (41) по z, получим

U_z(0, 0, 0) = kσ , (42)

Будем полагать, что отклонения ∆h = z(r, α) - h действительной поверхности от плоскости на глубине h малы по сравнению с h. При этом допущении подынтегральное выражение (42) может быть разложено в ряд Тейлора по степеням отношения ∆h/r

- = + + …

Ограничиваясь в разложении членами с ∆h в первой степени и подставляя их в формулу (36), получаем

U_z(0, 0, 0) = kσ , (43)

Положим

σ∆h = μ(r, α, h),

где μ(r, α, h) - поверхностная плотность плоского слоя, расположенного на глубине h. ,

Так как значение силы тяжести на поверхности плоского слоя

U_z(r, α, h) = 2πkμ = 2πkσ∆h, (44)

то формула (43) принимает вид

U_z(0, 0, 0) = . (45)

В случае двухмерной задачи

U_z(0, 0) = 2kσ = kσ . (46)

Подынтегральное выражение (46) разлагаем в ряд, считая, что отклонения контактной поверхности от плоскости ∆h(ξ) = η(ξ) - h малы по сравнению с h. Получаем

U_z(0, 0) = kσ = kσ . (47)

Ограничиваясь первым членом разложения и вводя поверхностную плотность μ(ξ, h) = σ∆h(ξ), находим

U_z(0, 0) = , (48)

где

U_z(ξ, h) = 2πkσ∆h(ξ) = 2πkμ(ξ, h) - значение U_z в точках плоскости ζ = h.

Полученные выражения (45), (48) являются не чем иным, как интегралом Пуассона [см. формулу (1.115)].

Таким образом, упрощение задачи об определении контактной поверхности свелось к трансформированию наблюденных значений силы тяжести к некоторой вспомогательной поверхности на глубине h. Такое упрощение позволяет применять для решения задачи различные методы аналитического продолжения аномалий cилы тяжести в нижнее полупространство на некоторую глубину h. Затем, используя формулу ∆h = U_z(r, α, h)/2nkσ, находят превышения рельефа относительно выбранной вспомогательной поверх­ности. Полученное таким образом решение задачи можно уточнить методом последовательных приближений.

Следует заметить, что метод последовательных приближений можно использовать для нахождения рельефа контактной поверхности и без предварительного определения U_z(r, α, h) на вспомога­тельной плоскости h. В этом случае за первое приближение (h) принимают наблюденное значение U_z и, используя формулу (44), строят рельеф контактной поверхности. При этом, естественно, должны быть известны избыточная плотность и глубина границы хотя бы в одной точке. Используя методы решения прямой задачи, вычисляют гравитационный эффект полученной в первом при­ближении контактной поверхности. Находя разность наблюденного и вычисленного значений аномалий силы тяжести ∆ = U_z - , в качестве второго приближения аналитически продолженного зна­чения берут (h) = U_z + ∆ = 2U_z - и строят новую поверх­ность, гравитационный эффект которой также можно подсчитать. Для последующих приближений

(h) = 3U_z - - ,

(h) = 4U_z - - - , (49)

……………………………….,

(h) = nU_z - - - ….. - .

Легко доказать, что процесс является сходящимся.

Число приближений зависит от сложности рельефа контактной поверхности, ее средней глубины и относительных превышений. При сравнительно спокойном рельефе для приблизительной оценки часто применяют самую простую формулу U_z = 2πkσ∆h, т. е. предпола­гают прямую пропорциональность между изменением аномалий силы тяжести и глубиной. Следует отметить, что эта формула дает результат тем точнее, чем меньше средняя глубина контактной поверхности. Рассмотрим для примера контактную поверхность в виде вертикального уступа.

Пусть x₁ и х₂ - координаты точек, расположенных по обе стороны от вертикальной границы уступа; h₁ и h₂ - глубина уступа в этих точках. Можно написать

U_z(+∞) – U_z(-∞) = 2πkσ(h₂ – h₁),

при больших значениях x₁ и х₂

U_z(x₂) – U_z(x₁) ≈ 2πkσ(h₂ – h₁). (50)

Заменяя вертикальный уступ материальной плоскостью на глу­бине h = (h₂ + h₁)/2 и фиксируя точки x₁, и x₂, получаем, что наиболее точно соотношение (50) выполняется при минимальной глубине материальной полуплоскости, поскольку в этом случав аномалии U_z меняется наиболее резко и быстро приближается к своим предельным значениям. Если глубину залегания материальной полуплоскости увеличивать, то изменение кривой U_z над уступом (материальной полуплоскостью) становится все более плавным, предельные значения достигаются при больших x₁, и x₂, разность U_z(x₂) – U_z(x₁) отличается от предельного значения все больше, причем всегда

U_z(x₂) – U_z(x₁) < 2πkσ(h₂ – h₁).

Из приведенного рассуждения следует, что гравитационный эффект контактной поверхности зависит также от средней ее глубины и применение формулы (44) для построения первого приближения контактной поверхности будет давать удовлетворительные резуль­таты только при неглубоком залегании контактной поверхности.

Если известна средняя глубина контактной поверхности h, то можно получить более точную формулу для вычисления превышений ∆h. Рассмотрим такой случай на примере двухмерной задачи.

Положим, что относительно средней глубины h превышение контактной поверхности h - ζ вдоль линии профиля, совпадающего с осью x, характеризуется следующей функцией:

h – ζ = ∆hcosωξ.

Тогда гравитационное действие контактной поверхности можно рассматривать как действие материальной плоскости, расположенной на глубине h и имеющей переменную поверхностную плотность

μ = σ∆hcosωξ = μ₀cosωξ.

В этом случае гравитационное действие этой плоскости на самой плоскости

U_z(ξ, h) = 2πkμ = 2πkμ₀cosωξ,

а на поверхности наблюдений на основании интеграла Пуассона

U_z(0, 0) = = 2πkμ₀e^-ωhcosωξ = U_z(h) e^-ωhи

или

U_z(0, 0) = 2πkσ (h – ζ), (51)

где

= ω.

Полагая в точках х₁ и х₂ глубину контактной поверхности соот­ветственно h₁ и h₂, получаем

U_z(x₂) - U_z(x₁) ≈ 2πkσ (h₂ – h₁). (52)

Это выражение является обобщением формулы (50), которая получается из него при условии

→ 1,

т. е. при h → 0 или l → ∞.

Таблица

Зависимость аффективной плотности от глубины контактной поверхности

h/l	σα/σ	h/l	σα/σ	h/l	σα/σ
0,00 0,05 0,10 0,15	1,000 0,730 0,534 0,381	0,20 0,25 0,30 0,40	0,284 0,208 0,150 0,081	0,50 0,75 1,00	0,043 0,009 0,002

При выполнении этих условий, т. е. при уменьшении средней глубины контактной поверхности (h → 0) или при увеличении поперечных размеров элементов рельефа этой поверхности (l → ∞),

повышается точность формулы (50). В пределе получается вертикальный уступ (горизонтальный слой), которому соответствует формула (50).

По упрощенной формуле (50) значения превышений контактной поверхности относительно ее сред­ней глубины получаются заниженными и это занижение тем больше чем глубже контактная поверхность При оценке гравитационного дей­ствия контактной поверхности по формуле (50) без учета средней

глубины всегда получаются завышенные значения гравитационной эффекта. Таким образом, реальная оценка гравитационного влияния контактной поверхности должна базироваться не только на учете избыточной плотности этой поверхности, но и на учете ее средней глубины. Если под эффективной плотностью контактной поверхности понимать

σ_α = σ

то можно отметить, что при прочих равных условиях эффективная плотность уменьшается с глубиной контактной поверхности (см. таблицу).

З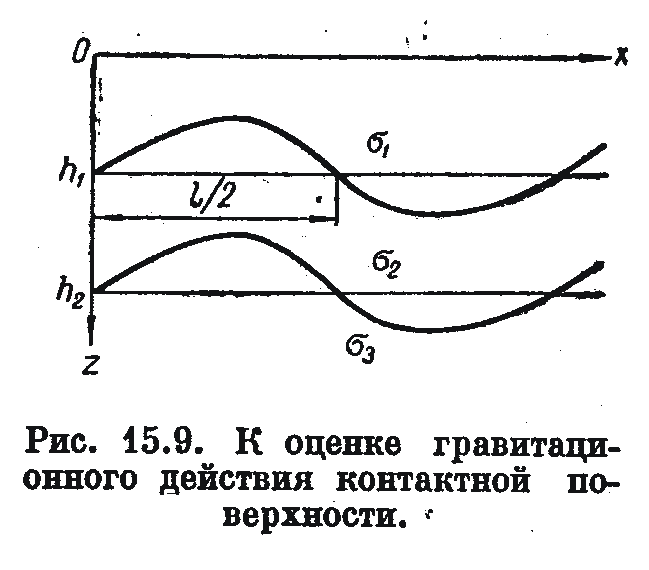 ависимость эффективной плотности от глубины границы раздела особенно важно иметь в виду при оценке гравитационного действия структур, у которых эти границы подобны друг другу. Не учет средних глубин залегания отдельных границ в этом случае может привести к существенным ошибкам. Действительно, обозначая средние глубины залегания границ h₁, h₂, . . ., h_n, избыточные плотности σ₁, σ₂, . . ., σ_т «период» контактной поверхности l, для такой структуры на основании формулы (52) можно написать

U_z(x₂) - U_z(x₁) = 2πkσ_α(h_i2 – h_i1),

где

σ_α = σ_i,

h_i1 и h_i2 - глубины залегания любой из поверхностей соответственно в точках x₁ и x₂.

Пусть

σ₁ = σ₂ = σ₃ = σ, h₁ = = = h, = 0.1.

Тогда по формуле (52) получим

U_z(x₂) - U_z(x₁) = 2πkσ( + + )(h_i2 – h_i1) = 0.972πkσ(h_i2 – h_i1)

Формула же (50) дает

U_z(x₂) - U_z(x₁) = 3∙2πkσ_α(h_i2 – h_i1),

Таким образом, действительный гравитационный эффект струк­туры в три раза меньше, чем вычисленный по формуле (50). При этом влияние верхней контактной поверхности оказывается наиболь­шим по сравнению с влиянием двух других поверхностей. Отсюда следует, что при определении контактной поверхности всегда следует стремиться найти реальную зависимость аномалий U_z от глубины контактной поверхности, используя известные значения глубины этой поверхности в некоторых точках исследуемого района. Коэф­фициент пропорциональности между U_z и ∆h в действительности всегда меньше 2πkσ.

Вертикальный уступ является предельным случаем структур флексурообразного типа, что позволяет использовать формулы, выражающие гравитационное действие уступа, в качестве оценочных для вычисления предельно возможной глубины этих структур. Из формулы

U_{xz max} = 2kσln

для произвольной флексурообразной структуры, имея в виду, что Н = h₂ – h₁, получаем

h₁ ≤

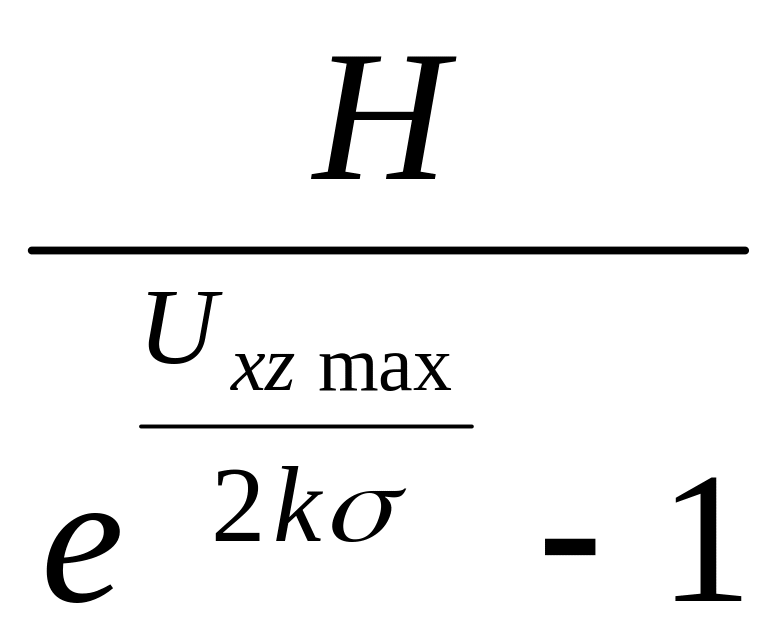
и, так как

H = ,

то

h₁ ≤ .

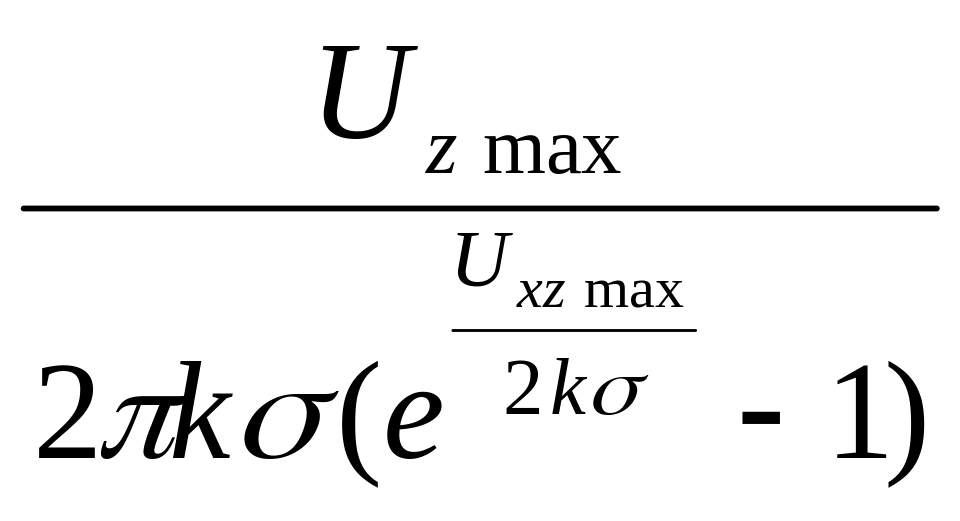Разлагая в ряд по степеням U_{xz тах}/2kσ и, ограничиваясь в разложении тремя первыми членами, имеем

h₁ ≤ 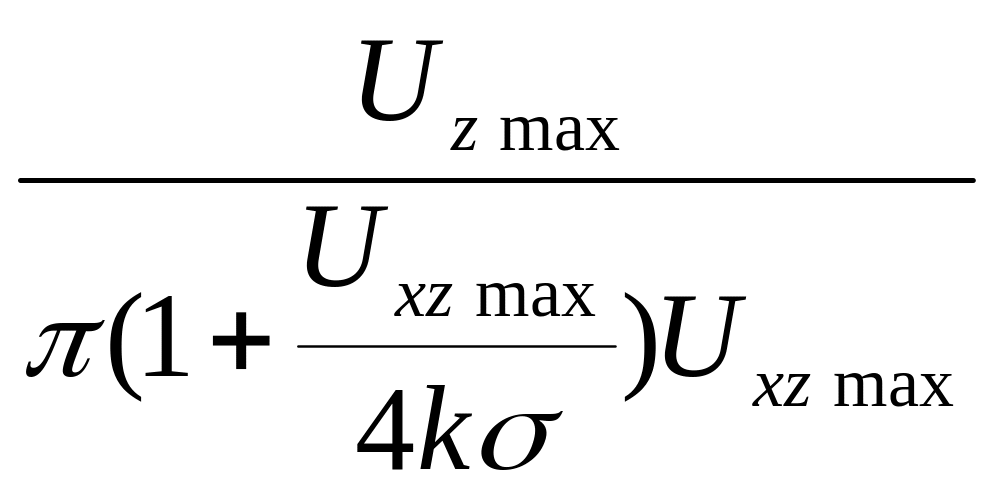. (53)

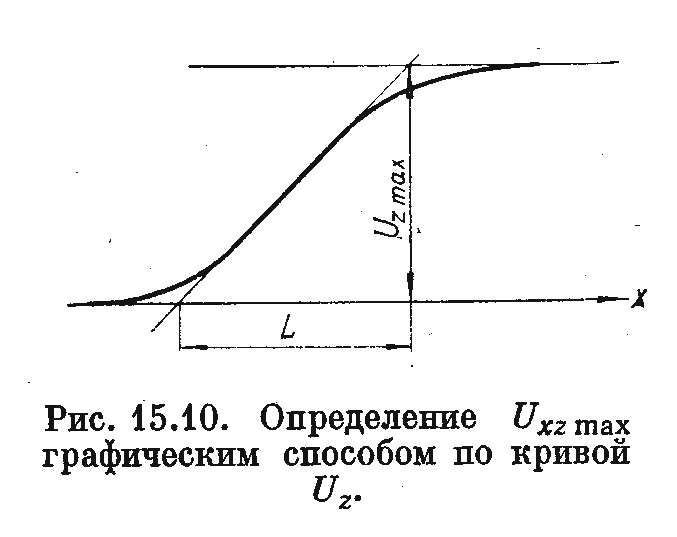
Значение U_{xz max} можно опреде­лить по кривой U_z графически:

U_{xz max} = .

Тогда формула (47) примет вид

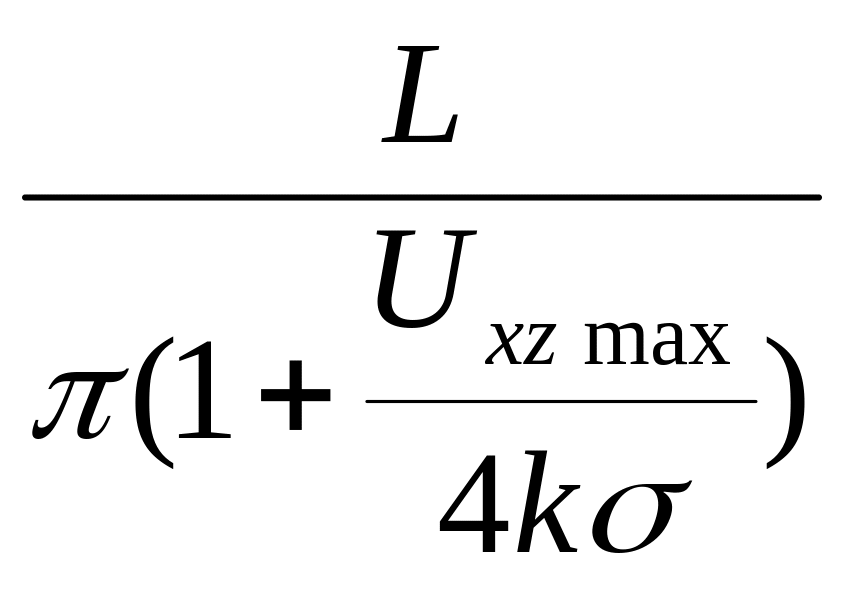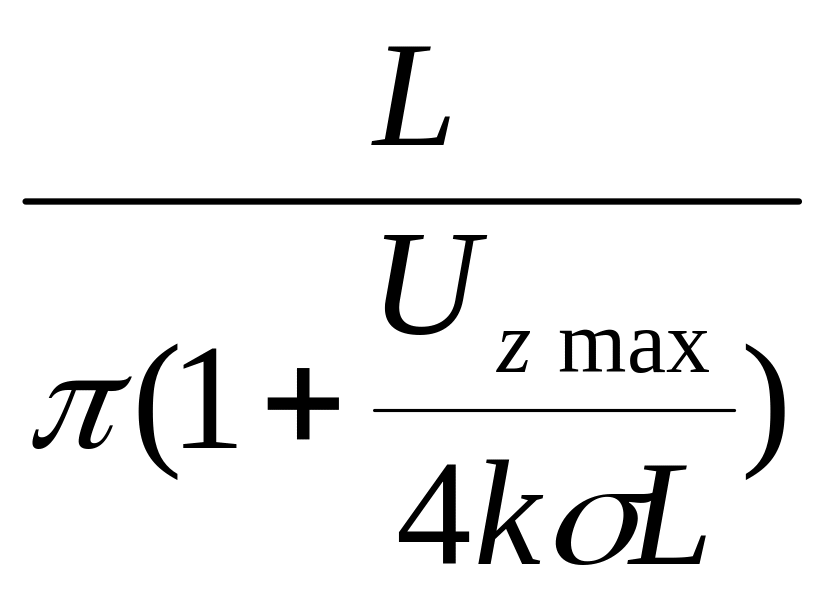h₁ ≤ = . (54)

По этой формуле можно оценивать предельную глубину масс любой формы, но чем больше отличается структура от вертикального уступа, тем приближеннее такая оценка.