46

Интерпретация гравитационных аномалий тел произвольной формы.

§1. Графические способы вычисления гравитационного эффекта тел произвольной формы

Реальные геологические объекты, создающие гравитационные аномалии, могут быть уподоблены телам правильной формы только приближенно, и полученные параметры геологических объектов дают в большинстве случаев лишь самое общее представление об их действительных размерах. Уточнить параметры тела можно, если подобрать тело, аномалия oт которого совпадает с наблюденной. Последовательно изменяя форму тела, можно добиться близкого совпадения наблюденной и вычисленной кривых. Совпадение ука­занных кривых позволяет утверждать, что полученная конфигурация тела отвечает форме реального геологического объекта.

Таким образом, чтобы определить параметры тела произвольной формы, необходимо уметь вычислить гравитационный эффект тела любой конфигурации. Все способы вычисления основаны на замене гравитационного действия такого тела действием суммы тел простей­шей формы, эффект которых может быть точно или приближенно вычислен. В большинстве случаев для этого используют различные вспомогательные графики-палетки. С их помощью тело произволь­ной формы легко может быть разбито на элементы, которые оказы­вают одинаковое гравитационное действие на точку, в которой надо вычислить аномалию. Очевидно, гравитационный эффект тела произвольной формы равен эффекту одного элемента равного действия, умноженному на сумму элементов, заключенных в объеме тела.

Рассмотрим сначала способы, которыми вычисляют гравитацион­ное действие двухмерных тел произвольной формы.

В полярных координатах производные гравитационного потен­циала принимают вид

U_z(0, 0) = ∆g(0, 0) = 2kσ ,

U_xz(0, 0) = 2kσ , (1)

U_zz(0, 0) = -2kσ ,

Проинтегрировав эти выражения по ρ в пределах от ρ_n до ρ_n+1 и по φ в пределах от φ_m до φ_m=1, получим гравитационное действие тела бесконечного простирания, имеющего сечение в виде кольцевого сектора:

U_{z mn}(0, 0) = 2kσ(cosφ_m - cosφ_m+1)(ρ_n+1 – ρ_n),

U_{xz mn}(0, 0) = kσ(cos2φ_m – cos2φ_m+1)ln , (2)

U_{zz mn}(0, 0) = kσ(sin2φ_m – sin2φ_m+1)ln .

Если построить окружности такими радиусами, чтобы ρ_n+1 – ρ_n = ∆ρ, и провести радиусы так, чтобы cosφ_m - cosφ_m+1= ,

(где m - число секторов, на которое разбивается квадрант), то гравитационное действие полученной элементарной площадки

U_{z mn}(0, 0) = 2kσ .

На радиусы и углы палеток U_xz и U_zz накладываем следующие условия:

ln = α, cos2φ_m – cos2φ_m+1) = , U_{xz mn}(0, 0) = kσ . (3) Сравнивая второе и третье выражения из формулы (2), получаем

sin2φ = cos2(φ - 45^е),

откуда следует, что для вычисления U_zz можно использовать ту же самую палетку, что и для U_xz, повернув ее на 45°.

Положив в формулах (2) U_{z mn} = 1 мгал и U_{xz mn} = 1 этвеш, получим уравнения для определения ∆ρ, φ и ln , φ. Каж­дое такое уравнение содержит два неизвестных: ∆ρ и φ или и φ. Поэтому для одних и тех же значений U_{xz mn} и U_{z mn} можно построить площадки разной формы. Для того, чтобы погрешность при подсчете площадок, попадающих в контур тела, сделать минимальной, необходимо придать площадкам форму, близкую к ква­дратной. Это может быть выполнено наложением дополнительного условия, связывающего ρ и φ: разность двух соседних радиусов должна быть равна дуге среднего радиуса

ρ_n+1 – ρ_n = (φ_m+1 – φ_m) ,

откуда следует

= ,

где ∆φ_m = φ_m+1 – φ_m.

Логарифмируя это равенство и разлагая правую его часть в ряд по степеням ∆φ_m, получаем

ln = ∆φ_m(1 + (∆φ_m)² + …)

или

ln = ∆φ_m = φ_m+1 – φ_m.

И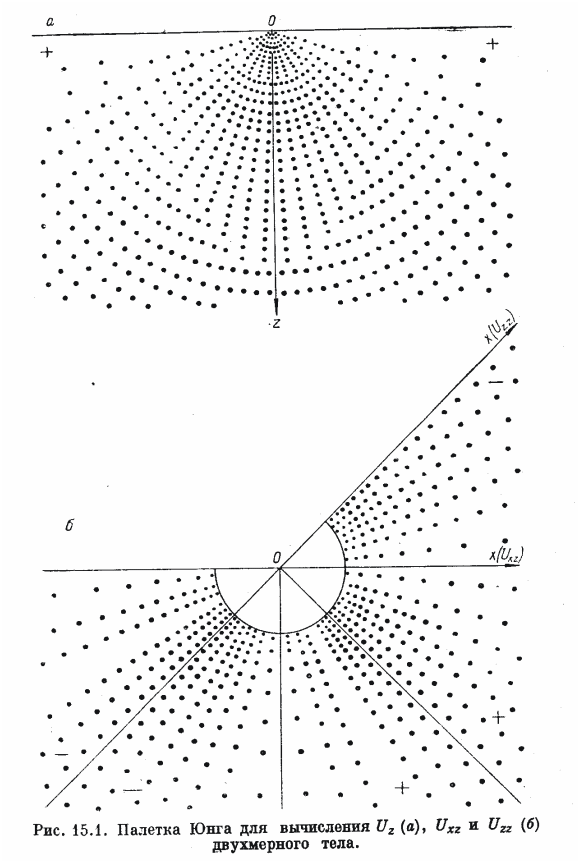 спользуя это уравнение, получаем единственную систему радиусов и лучей, определяющих границы площадок равного действия.

Следует иметь в виду, что при изменении φ от нуля до π/2

cos2φ_m - cos2φ_m+1 > 0,

а в интервале от π/2 до π

cos2φ_m - cos2φ_m+1 < 0.

Таким образом, при изменении φ от нуля до π/2, U_xz имеет положительные значения, а от π/2 до π - отрицательные. Для палетки U_zz положительные значения U_zz соответствуют интервалу φ от π/4 до ³/₄π, отрицательные - от нуля до π/4 и от ³/₄π до π. Чтобы проще было считать, на палетках вместо площадок указаны точками их центры.

Палетки обычно рассчитывают для плотности σ₀ = 1 г/см³. Для конкретного объекта результат вычислений по палетке необходимо умножить на отношение σ/σ₀, где σ₀ - плотность, для которой рассчитана палетка; σ - плотность геологического объекта.

При использовании палеток для вычисления U_xz и U_zz масштаб разреза не влияет на окончательный результат, так как в формулы входит отношение , а не сами эти величины. Необходимо только, чтобы вертикальный и горизонтальный масштабы разреза были одинаковы. С укрупнением масштаба разреза контур тела ложится на более далекие точки, но количество точек, попадающих в контур тела, остается одним и тем же. Поэтому, если контур тела располагается близко к центру палетки, то для повышения точности вычислений U_xz и U_zz масштаб разреза следует укрупнить.

Иначе обстоит дело с палетками для вычисления U_z. В формулу (2) множителем входит разность радиусов ρ_n+1 – ρ_n. Палетку U_z строят в определенном линейном масштабе. Если масштаб разреза не соответствует масштабу палетки, то окончательный результат вычислений по палетке необходимо умножить на М/М_о, где М_о - масштаб палетки; М - масштаб разреза тела.

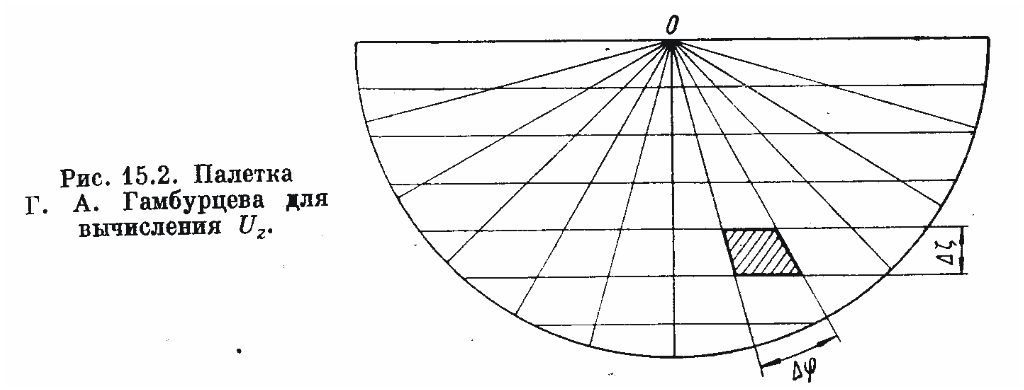
Приведенные выше полярные палетки для двухмерных тел впервые были предложены К. Юнгом. Весьма простая для построения палетка U_z от двухмерных тел рассчитана Г. А. Гамбурцевым. Принцип ее состоит в следующем.

В формуле (1) положим

ζ = ρsinφ

тогда

dζ = sinφdρ,

U_z(0, 0) = 2kσ = 2kσ = 2kσ(ζ_n+1 – ζ_n)(φ_m+1 – φ_m).

Полагая

ζ_n+1 – ζ_n = ∆ζ и φ_m+1 – φ_m = ∆φ = ,

имеем

U_{z mn}(0, 0) = 2πkσ .

Техника построения палетки очень проста. Через равные интер­валы ∆ζ проводят горизонтальные линии, и через равные углы из центра палетки О проводят лучи. Таким образом, вся плоскость оказывается разбитой на площадки равного действия. Некоторый недостаток этой палетки по сравнению с полярными палетками состоит в том, что сильно вытянутая форма площадок по краям палетки приводит к большим погрешностям при подсчете гравитационного эффекта.

Д. Бартон предложил и разработал методику построения палеток для вычисления U_xz и U_zz, представив пространство в виде прямо­угольных призм равного действия. Исходными служат формулы для прямоугольного параллелепипеда.

U_z(0, 0) = σk(ξ₁ln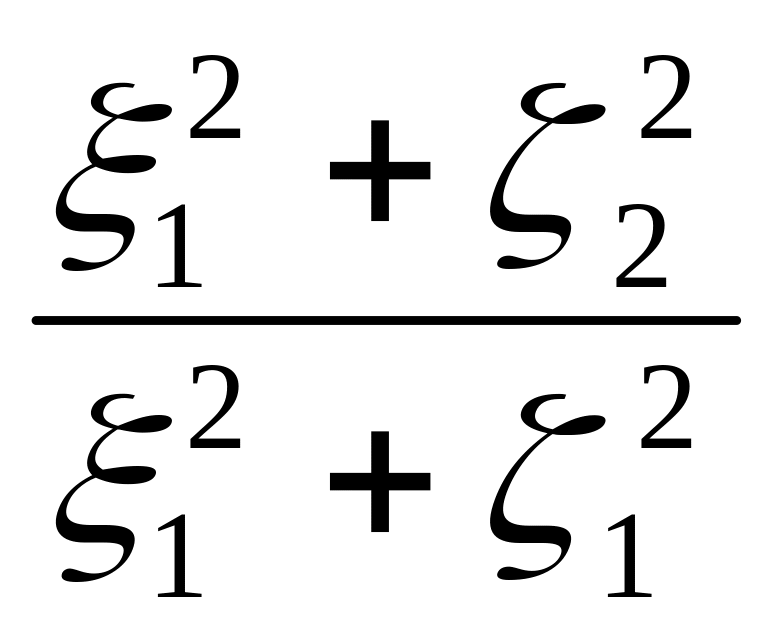 - ξ₂ln 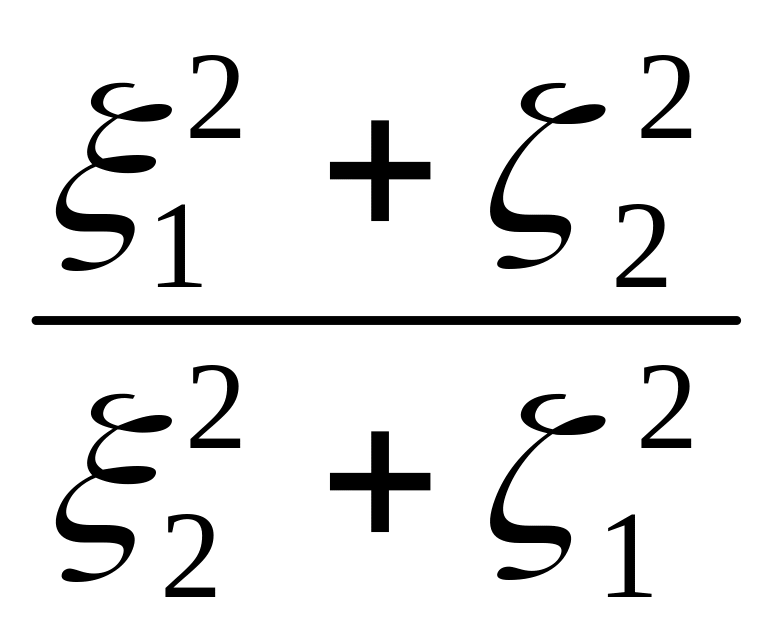+ 2ζ₂(arctg arctg ) + 2ζ₁(arctg arctg )),

U_xz(0, 0) = σkln ,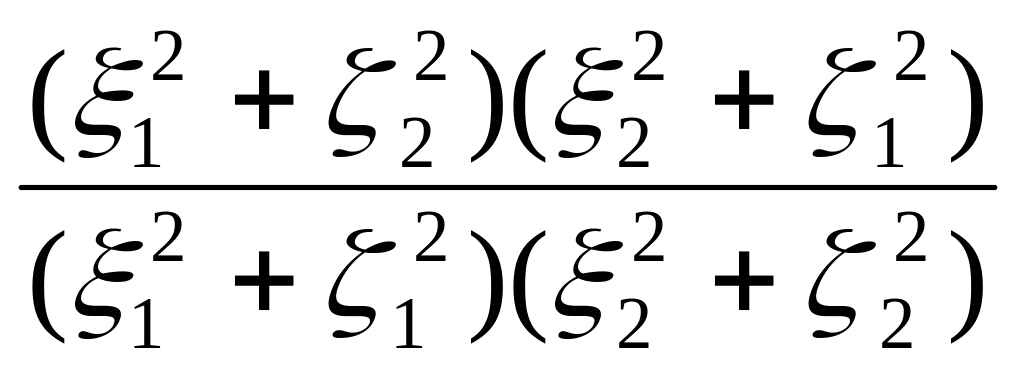

U_zz(0, 0) = 2σk(arctg arctg + arctg arctg ),

Положим, что одна из граней прямоугольного параллелепипеда совпадает с координат­ной плоскостью yOz, тогда ξ₁ = 0. Помещая начало координат в точку наблюдения, получаем

U_xz(0, 0) = σkln ,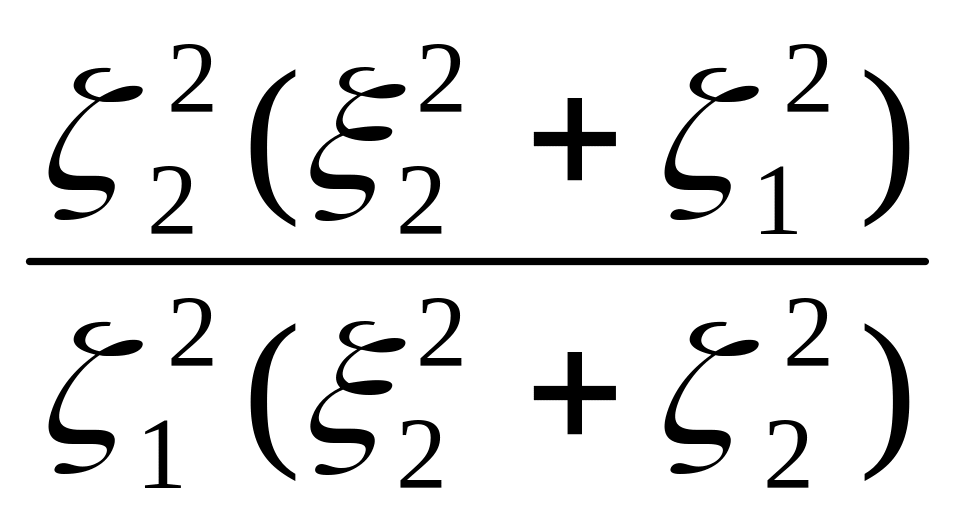

U_zz(0, 0) = 2σk(arctg arctg ). (4)

Введем обозначения

= A, = u

Тогда формулы (4) принимают вид

U_xz(0, 0) = σkln ,

U_zz(0, 0) = 2σk(arctg arctg ). (5)

Задаваясь величиной A, можно выбрать u таким образом, чтобы U_xz и U_zz принимали определенные значения N. Полагая в равен­ствах (5) U_xz = N_xz и U_zz = N_zz и вводя соответственно обозначения

p_xz = , p_zz = tg , (6)

для постоянного А находим величины u.

Для аномалии U_xz

u = ±A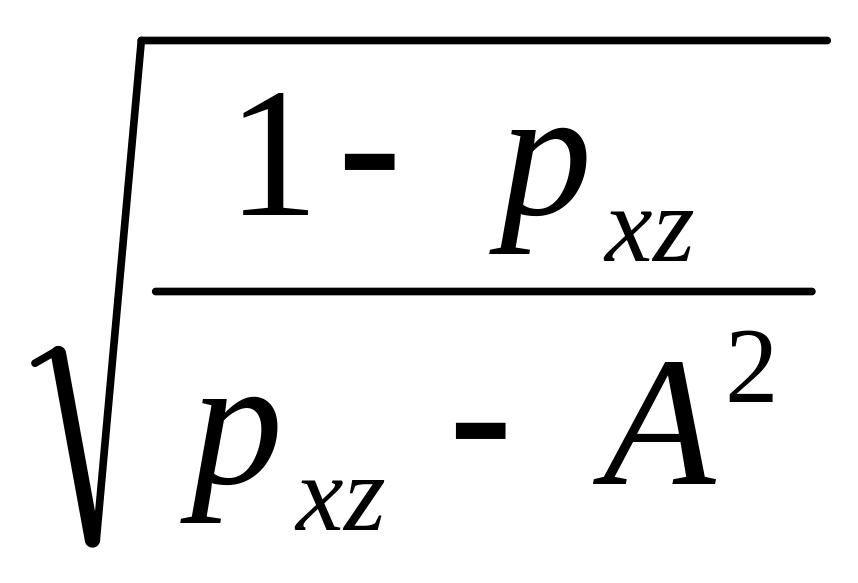 . (7)

Для аномалий U_zz

u = ± . (8)

Используя соотношения (6), (7), (8), можно для любых заданных значений А и N определить u. При этом полагают σ = 1 г/см³. Выбирая произвольно А и принимая N равным последовательно 1, 2, 3. . . этвеш, находим соответствующие им значения u₁, u₂, u₃ … которые определяют на плоскости xOz систему прямоугольников, действие каждого из которых на начало координат равно 1 этвеш.

П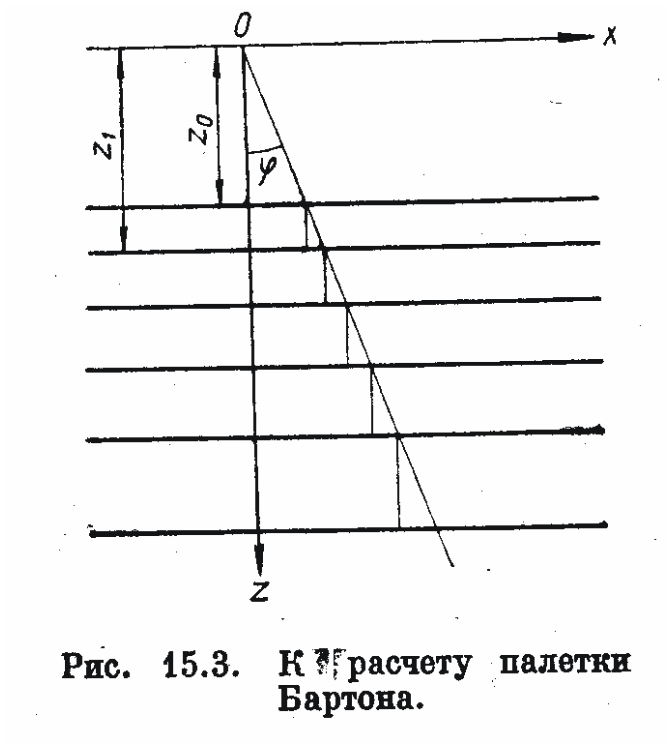 остроение палеток Бартона сводится к следующему. В прямоугольной системе координат xOz параллельно оси х проводим ряд прямых, определяемых значениями

z₀ = z₀, z₁ = Az₀, z₂ = A²z₀, z₃ = A³z₀, …., z_n = Aⁿz₀.

Величины А и z₀ выбирают произвольно. Однако для палетки U_xz целесообразно выбрать А так, чтобы действие каждого из бесконечных слоев было равно целому числу N этвеш. Для этого, полагая в фор­муле (7) u = ∞, находим А = . При построении па­летки U_zz следует А выбрать так, чтобы максимальное значение U_zz, определяемое формулой (5), выразилось также целым числом N этвеш. Из уравнений (6) и (8) получаем

A = .

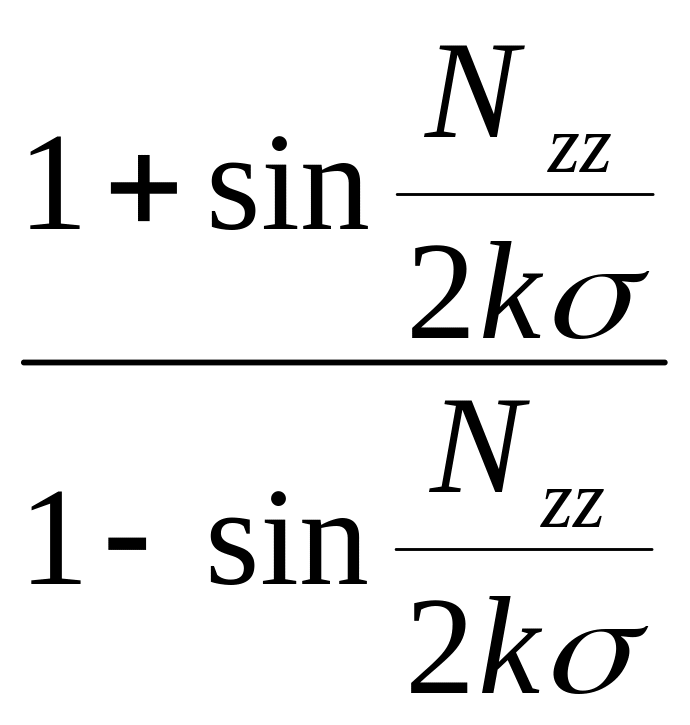Пользуясь формулами (7) и (8) при N = 1, 2, 3 . . ., на­ходим u₁, u₂ . . . Из начала координат проводим прямую, составля­ющую с осью z угол φ, определяемый условием

tgφ= u.

Поскольку ξ₂ = uζ₁, то, опуская перпендикуляры из точки пересечения этой прямой с прямыми, заданными уравнениями z_n = = Aⁿz₀, получаем ряд прямоугольников, каждый из которых ока­зывает на начало координат гравитационное действие U_xz или U_zz, равное 1 этвеш.

Для вычисления гравитационного эффекта трехмерных тел можно построить палетки, аналогичные рассмотренным. В частности, для трехмерных тел, уподобляемых цилиндрам, т. е. нормальное сечение которых не меняется по простиранию, рассчитывают полярные палетки. В этом случае, полагая, что размеры тела по простиранию равны 2b, а профиль проходит над серединой тела, из выражения для стержня конечной длины

U_z(0, 0, 0) = 2kλ f₁(b),

где f₁(b) = ,

имеем

U_z(0, 0, 0) = 2kσ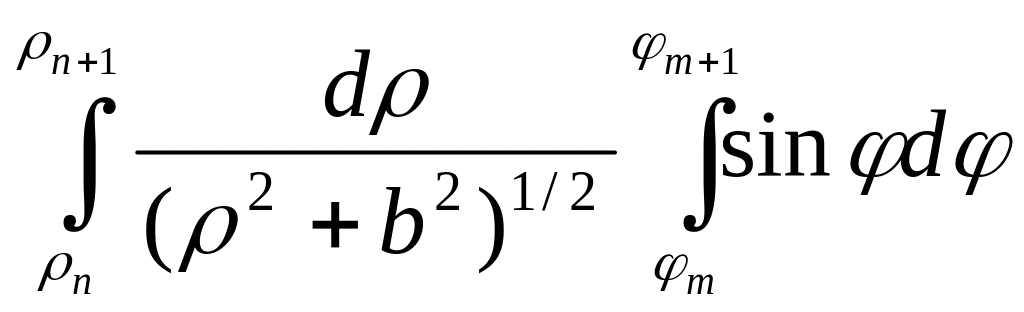 . (10)

После интегрирования по р и ср получаем

U_z(0, 0, 0) = 2kσ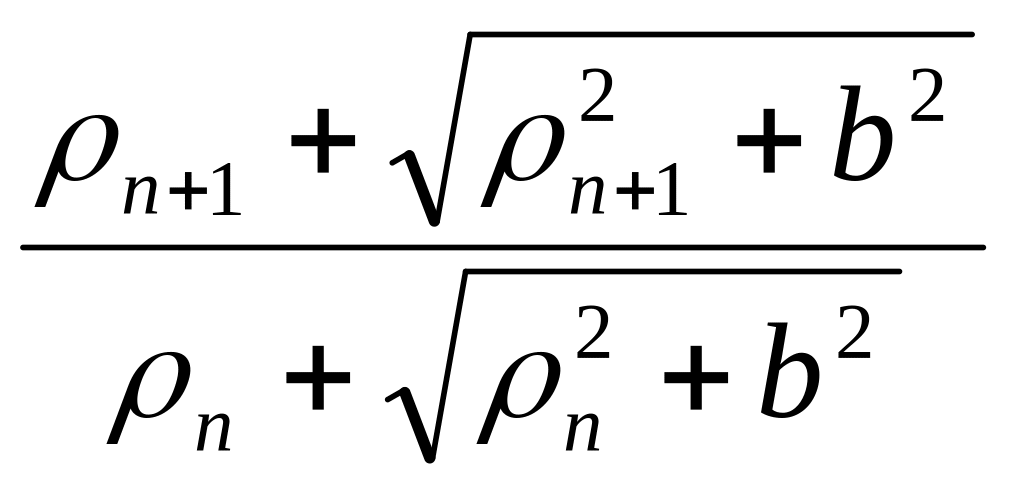 (cosφ_m+1 – cosφ_m).

Задавая b различные значения, построим полярные палетки для вычисления U_z(0, 0, 0).

Следует заметить, что вторые производные от трехмерных тел в практике интерпретации вычисляют сравнительно редко, поскольку влияние конечных размеров тела на характер вторых произ­водных, особенно на U_xz, сказывается значительно слабее, чем на U_z. Однако для цилиндрических тел с конечным простиранием существуют палетки Бартона. Кроме того, для вычисления эффекта трехмерных тел можно использовать графический способ Самсонова, рассмотренный при учете влияния рельефа на показания гравита­ционного вариометра.

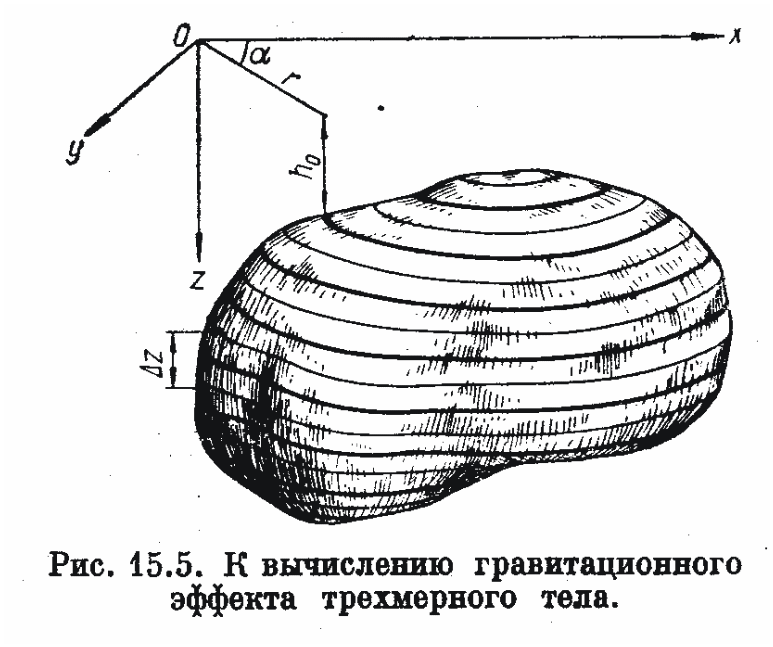Рассмотрим еще один способ вычисления гравитационного эффекта U_z трехмерных тел. Разобьем трехмерное тело горизонталь­ными плоскостями на слои толщиной ∆z. Действие каж­дого реального слоя можно заменить действием материального слоя, расположенного на средней глубине z = h₀ и имеющего поверх­ностную плотность μ = σ∆z. На этом принципе основано несколько типов палеток, различающихся формой площадок равного действия. Е. А. Мудрецовой построены палетки в цилиндрической системе координат, площадками равного действия являются секторы. В палетках А. К. Маловичко и О. Л. Таруниной площадки представляют собой квадраты.

В качестве примера рассмотрим способ построения палетки Е. А. Мудрецовой для вычисления U_z. Располагая начало координат в точке наблюдения, для одного материального слоя имеем

U_z(0, 0, 0) = k . (11)

Интегрируя по r в пределах от r_n до г_п+1 и по α в пределах от α_m до α_ь+1, получаем U_z от элементарной площадки слоя

U_{z mn}(0, 0, 0) = kμh₀( - )(α_m+1 - α_m). (12)

Проведем радиусы r через равные углы

α_m+1 - α_m =

и положим

- = c_mn,

тогда

U_{z mn}(0, 0, 0) = = c_mn.

Чтобы получить притяжение всего материального слоя, нужно определить число N элементарных площадок, умещающихся на площади слоя,

U_z(0, 0, 0) = c_mnN. (13)

Палетки для h r₀ = 1, 2, … единиц масштаба, в котором построено тело. Горизонтальные сечения тела изображают в виде карты изоглубин через интервалы ∆z = 1, 2, ... единиц масштаба чертежа. По палетке, соответствующей данной глубине h₀, подсчитывают гравитационный эффект каждого материального слоя и результаты суммируют. Можно исполь­зовать и одну палетку, но при этом следует каждый контур материального слоя строить в своем масштабе глубины h₀. Трехмерное тело можно разделить не только на горизонтальные пласты постоянной мощности, но и на вертикальные столбики. Сечение столбиков в горизонтальной плоскости представляет собой кольцевые секторы с радиусами r_n и r_n+1 и углами α_m и α_m+1, а высота столбиков равна разности глубин верхней h₁ и нижней h₂ граней тела. Помещая начало координат в точку наблюдения, для элементарного столбика имеем:

U_{z mn}(0, 0, 0) = kσ .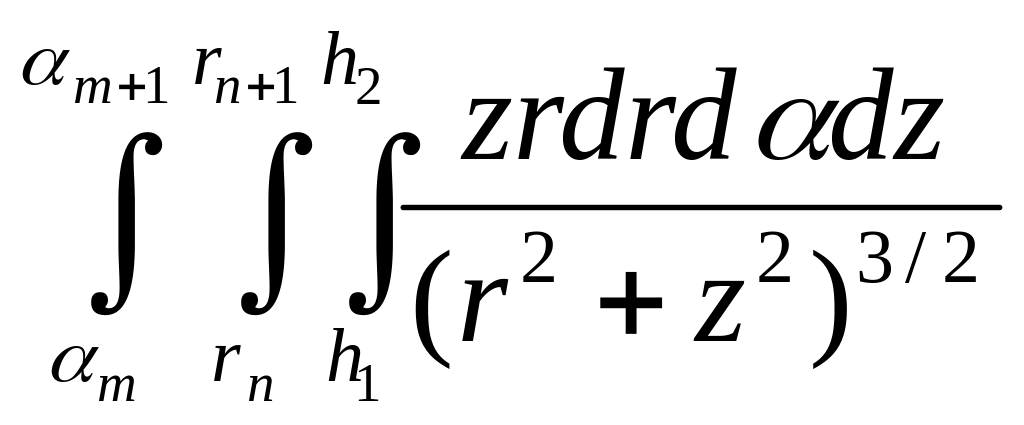

После интегрирования в указанных пределах получаем

U_{z mn}(0, 0, 0) = kσ( - - + )(α_m+1 + α_m).(14)

Вводя обозначения

- = c_mn,

- = c^/_mn (15)

и разбивая окружность радиуса г на равные углы

α_m+1 – α_m = , (16)

получаем

U_{z mn}(0, 0, 0) = (c_mn - c^/_mn).

Для всего тела

U_z(0, 0, 0) = (c_mn - c^/_mn). (17)

Выбрав радиусы г_n и г_п+1, для различных h строим таблицу с_mn. Накладываем палетку на план изоглубин верхней и нижней поверхностей тела. По значениям h, определенным в середине площадки, в таблице находим с_mn для структурного плана верхней границы тела и с^/_mn для нижней границы. Суммируя с_mn и с^/_mn по формуле (17), определяем окончательное значение U_z(0, 0, 0).