1.1.7 Зависимость теплового эффекта реакции от температуры

Приведенные ранее способы расчета тепловых эффектов применимы для определения Н при постоянной температуре (чаще всего стандартной, 298 К).

При температурах, отличных от стандартной, используют уравнение Кирхгофа.

В дифференциальном виде оно имеет вид,

(1.5)

где есть разность между суммарными теплоемкостями продуктов реакции (конечных веществ) и исходных веществ (начальных).

Анализ уравнения (1.5):

1. Если С_Р >0, то первая производная > 0, следовательно функция Н растет с ростом температуры, то есть тепловой эффект возрастает, независимо от знака самого теплового эффекта (рисунок 1.2 а).

2. Если С_Р < 0, то первая производная , следовательно функция Н убывает с ростом температуры.

3. Если С_Р= 0, то первая производная . В этом случае Н = const, то есть не зависит от температуры. Если при одной температуре, то при этой температуре будет экстремум (рисунок 1.2 б).

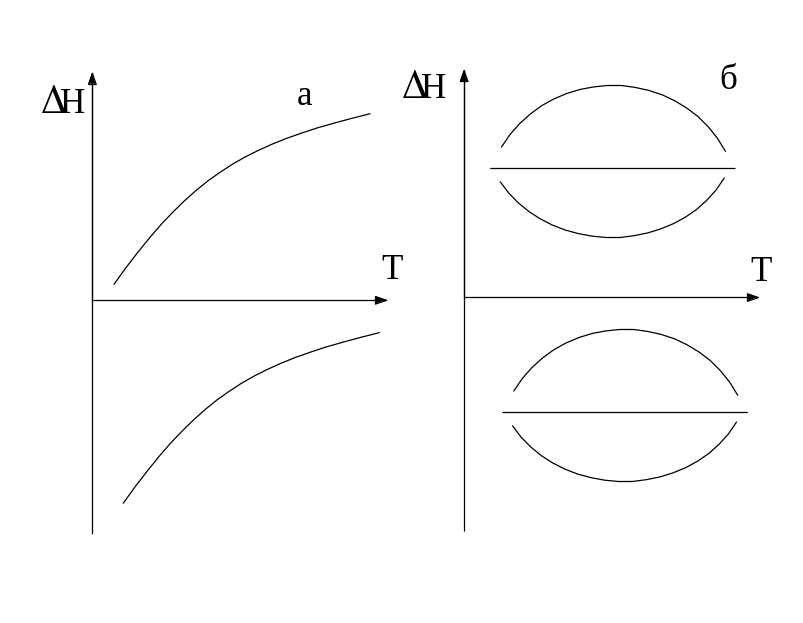
Рисунок 1.2 – Зависимость теплового эффекта от температуры

Интегрирование уравнения Кирхгофа приводит к уравнению, позволяющему рассчитать тепловой эффект реакции при любой температуре:

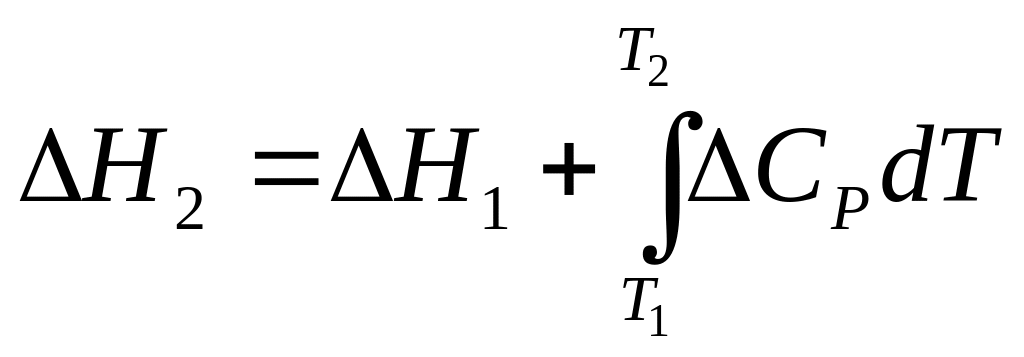(1.6)

где Н₂ - тепловой эффект реакции при любой температуре; H₁ - тепловой эффект реакции при Т₁, рассчитанный одним из ранее приведенных способов.

Расчет интеграла в уравнении 1.5 возможен с разной степенью точности:

1.

Это возможно в случае небольшого температурного интервала, а также в случае больших значений теплового эффекта, когда температурной зависимостью можно пренебречь.

2.

Если значение в данном температурном интервале неизвестно, можно принять .

3. . Обычно эта зависимость может быть получена из интерполяционных уравнений для С_р (1.4):

∆С_р = ∆а + ∆вТ +∆сТ² + ∆с^lТ ^-2 (1.7)

где ; Δв, Δс, Δс^l находятся аналогично.

Подстановка уравнения 1.7 в уравнение 1.6 и интегрирование дает развернутое уравнение Кирхгофа:

(1.8)

Анализ температурной зависимости ΔН = f(T)

1. Исследование на экстремум.

Признаком существования экстремума является обращение в ноль первой производной исследуемой функции ΔН = f (T), т.е. по уравнению (1.8).

Из уравнения Кирхгофа:

(1.9)

Приравнивая к нулю полученное выражение, рассчитывается температура, при которой производная обращается в ноль. Приближенно можно ограничиться двумя слагаемыми в уравнении (1.9), т.е. .

Если Т > 0 и ее значение лежит в интервале температур, в пределах которых действуют интерполяционные уравнения (интервалы указаны в справочнике), значит экстремум на кривой ΔН = f (T) существует. Для уточнения, какой именно экстремум (максимум или минимум) следует взять вторую производную и определить ее знак:

Если > 0, то имеет место минимум, если < 0, то максимум.

Если же Т < 0 или лежит вне интервала температур, значит экстремум отсутствует и в исследовании функции переходим к пункту 2.

2. Для определения возрастающей или убывающей функции следует определить знак первой производной:

В это уравнение подставляется любая температура, взятая внутри интервала, и рассчитывается : если > 0, то ΔН - возрастающая функция; если < 0, то убывающая функция.

Для уточнения хода кривой определяют вторую производную и ее знак:

> 0, то кривая вогнутая, при <0 - выпуклая.