Побудова матриць близькості для кількісних ознак
Мета роботи. Використовуючи створену таблицю експериментальних даних про різні досліджувані об’єкти та задану метрику побудувати матрицю близькостей (відстаней), застосовуючи нормування даних.
Характеристики мір.
Якщо
відстань між об’єктами природно
трактувати як міру відмінності об’єктів,
то обернену величину
можна розглядати як міру подібності
(близькості) об’єктів.
1.
Найчастіше відстань
між об’єктами вимірюють в евклідовій
матриці, яка найбільш узгоджена з нашими
інтуїтивними представленнями про
близькість об’єктів і визначається
, (4)
де
та
–
значення компонент в опису 1-го та 2-го
об’єктів,
–
розмірність простору ознак .
2. Широко використовується лінійна метрика (метрика міських кварталів або манхетенська метрика) яка задає відстань
, (5)
а також sup- норма , яка визначає чебишевську відстань
. (6)
На рис. 1. показано зміст цих відстаней.
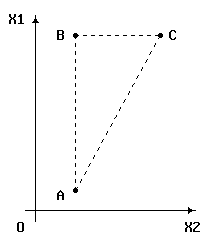
Рис.1.
Ілюстрація змісту відстаней
-
довжина
відрізка
АС;
-
сума
довжин
відрізків
АВ
і
ВС;
-
довжина
більшого
з
відрізків
АВ
і
ВС,
тобто
АВ.
Очевидно,
що
з ростом розмірності
манхетенська відстань
підкреслює, а чебишевська злагоджує
відмінності між об’єктами. Відстані
визначаються для тих описів , в яких
ознаки виражені кількісними шкалами і
є по-суті частинними випадками узагальнення
степеня відстані
Мінковського
,
для яких
отримуються при
.
Існує досить велика різноманітність
мір, але на практиці ці міри є найуживанішими.
Евклідова відстань ефективна при дослідженні слабокореляційних сукупностей об’єктів (кулеподібні класи), а манхетенська тоді, коли об’єкти утворюють плоскі витягнені класи, ортогональні будь-яким координатним осям простору ознак. Тому обробка однієї і тієї ж сукупності даних одним і тим же методом або алгоритмом, але з використанням різних метрик може дати різні, інколи кардинально протилежні, результати.
Наприклад. При використанні манхетенської метрики утворені класи витягнуті вздовж осі абсцис, а при використанні евклідової відстані об’єкти будуть згуртовані в два більш-менш рівні класи (пунктир). Отже, до вибору метрики слід підходити дуже продумано і обережно співставляючи результати використання різних метрик між собою із цілями здійснюваної обробки даних.
Якщо ознаки представляються в якісних шкалах, зокрема в шкалах найменувань та порядку, використовують відстань Хеммінга
для
якої відмінності виражаються числом
неспівпадінь властивостей порівнюваних
об’єктів. У випадку якісних шкал ознаки
розглядаються як бінарні, тобто такі,
що можуть приймати лише два значення
“ 0 “ та “ 1 “. Відстань Хеммінга
є максимальною і рівна
1
для об’єктів з протилежними за значеннями
описами, тобто елементи одного опису є
протилежними до відповідних елементів
опису другого об’єкту. Для об’єктів,
всі ознаки яких (з числа включених в
опис) співпадають,
.
Хід роботи.
1. Вибрати мову програмування та скласти план розробки програмного забезпечення для перетворення таблиці даних в матрицю близькості заданого типу: за видом метрики та способом нормування даних.
2. Розробити програмне забезпечення для побудови матриці близькостей, яке використовує вказану або вибрану метрику зчитує значення ознак з таблиці даних, нормує ці дані у відповідності з заданою формулою для нормування даних, визначає значення відстаней.
3. За отриманими даними побудувати матрицю відстаней, у формі придатній для подальшого програмного використання, тобто у формі файлу даних, які можна використовувати при роздруку як готову матрицю близькостей, а в програмах як файл даних.
4. В звіті представити вихідні дані у формі таблиці даних, опис метрики, пояснити метод нормування, привести алгоритм програмного забезпечення та матрицю близькостей. Для матриці близькостей дати коротке пояснення (які об’єкти є найближчі між собою, які найдальше, який зв’язок між об’єктами, тощо.), а звіт завершити короткими висновками.
ЛАБОРАТОРНА РОБОТА № 2.2