2.2.2. Криптография

Другим важным общим вопросом для источника информации является ее защита от несанкционированного доступа, т.е. придание свойства секретности при передаче информации.

Для этого существует криптография – раздел математики, в котором изучаются и разрабатываются системы изменения письма, позволяющие сделать его непонятным для непосвященных лиц.

Это особенно важно в связи с широким распространением компьютерных сетей.

Криптография – достаточно сложная наука, поэтому рассмотрим лишь ее основы.

Теоретические основы криптографии были разработаны К. Шенноном в 40-е годы прошлого века.

Существуют следующие варианты шифров информации.

1. Простая замена. Здесь система одних букв заменяется на систему других букв ил производится чтение в письме только определенных букв, например, каждой третьей, как у А. Конан Дойля в рассказе «Плящущие человечки». Такие шифры достаточно легко расшифровываются, если знать, на каком языке написано письмо. Так, в английском языке чаще всего встречается буква «о», а в английском – буква «е».

В усовершенствованных шифрах символы исходного сообщения заменяются на символы из определенного множества или текста. Они удлиняют сообщение и снижают скорость его передачи.

2. Шифры-перестановки. Например, фраза ТЕОРИЯ ИНФОРМАЦИИ разделяется на столбцы по 4 символа

ТЕОР

ИЯИН

ФОРМ

АЦИИ

Если теперь сообщение прочитать по столбцам, то получится ТИФАЕЯОЦОИРИРНМИ.

Такие шифры трудно расшифровать: необходимо знать дополнительную информацию. Однако, если удается расшифровать одно сообщение, то остальные расшифровываются легко.

Можно задавать ключевое слово, позволяющее определить порядок чтения столбцов. Например, если задать слово РЕКА, то сообщение получит вид

РЕИТ

НЯОИ

МОРФ

ИЦИА.

Нетрудно видеть, что здесь два уровня секретности: способ составления шифра и ключ. Последний может передаваться по другому засекреченному каналу.

Зашифруем ранее предложенное сообщение ключом КИБЕРНЕТИКА.

Т Е О Р И Я И Н Ф О Р М А Ц И И

20 6 16 18 10 33 10 15 22 16 18 14 1 24 10 10

К И Б Е Р Н Е Т И К А К И Б Е Р

12 10 2 6 18 15 6 20 10 12 1 12 10 2 6 18

32 16 18 24 28 15 16 2 32 28 19 26 11 26 16 28

Ю О Р Ц Ъ Н О Б Ю Ъ С Ш Й Ш О Ъ

Если использовать случайную последовательность, то шифр без ключа - нераскрываем. Проблема – в передаче ключа.

Предложена система шифрования без передачи ключа, имеющая три разновидности: без передачи ключа; с открытым ключом; электронная подпись.

Все системы построены по одному принципу, поэтому рассмотрим только шифрование без передачи ключа.

Пусть два абонента А и Б договорились о производстве закрытой переписки. Они выбирают простое и не большое число p, такое, что число (p - 1) разлагается на простые множители a и b, принимаемые абонентами А и Б. Числа a и b являются первыми секретными ключами абонентов.

Вторые ключи ( и  соответственно) находятся из уравнений a  1(mo(p)), 0 <  < p - 1 для А и b  1(mod(p)), 0 <  < p - 1. Если пересылаемое сообщение больше (p - 1), то оно разбивается на части, каждая из которых должна быть меньше (p - 1).

Пусть абонент А отправляет абоненту Б сообщение m, m < (p - 1), зашифровывая по формуле m₁ = m^a(mod(p)). Абонент Б, получив сообщение, зашифровывает его в виде m₂ = m₁^b(mo(p)) и отправляет абоненту Б. Абонент А шифрует это сообщение m₃ = m₂^(mo(p)) и отправляет окончательно абоненту Б, который, используя ключ , расшифровывает сообщение.

В самом деле, m₄ = m₃^ = m^ab(mod(p)), поскольку ab  1 (mod(p)) и ab = k(p) +1 для некоторого целого k, m^{k(p) +1}  (m^(p))^km(mod(p))  m из-за m^(p)  1 (mod(p)) по теореме Эйлера.

Пример 2.1. Пусть p = 23 ((23) = 22), a = 5, b = 7. Из 5 = 1 (mod (23)) получим  = 9, а из 7 = 1 (mod (23)) имеем  = 19. Пусть m = 17.

Т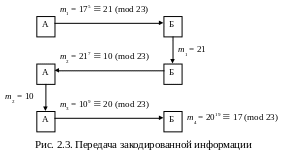 огда передача информации может быть отражена схемой, показанной на рис. 2.3.