Министерство образования и науки Российской Федерации
Волгодонский инженерно-технический институт
Национального исследовательского ядерного университета МИФИ
Утверждено
на заседании кафедры
« » 2011 г.
Методические указания
к выполнению лабораторных работ
по дисциплине «Инженерное обеспечение строительства (геодезия)»
(для студентов строительных специальностей)
Волгодонск 2011
Лабораторная работа № 1
РАБОТА С ТОПОГРАФИЧЕСКИМ ПЛАНОМ
1. Масштабы: численный, линейный и поперечный
2. Изучение условных знаков и чтения топографических планов
3. Задачи, решаемые по топографическому плану
а) определение прямоугольных координат точек на крупномасштабных топографических планах применяется зональная система прямоугольных координат. На планы наносят координатную сетку со сторонами 10 см. Вертикальные линии параллельны оси абсцисс, а горизонтальные - оси ординат. Координаты линий подписывают в зарамочном оформлении (между внутренней и внешней рамками плана).
Так на плане масштаба 1:2000 (рис, 4) линии координатной сетки подписаны в километрах через 0,2 км, соответственно по оси абсцисс 79,4; 79,6; ...80,2, а по оси ординат 66,0; 66,2; ...66,8.
Пользуясь циркулем и поперечным масштабом, можно по плану определить прямоугольные координаты точки А (рис.4) относительно координатной сетки. Сначала записывают абсциссу нижней (южной) линии квадрата, в котором находится точка А, в метрах. Например, 79800,0 м. Измеряют расстояние х в метрах по поперечному масштабу. Полученную величину, например, 90,8 м прибавляют к абсциссе линии. Тогда Ха = 79800,0 + 90,8 = 79890,8 м.
Аналогично определяют ординату точки А. К значению ординаты левой (западной) линии квадрата 66200,0 м прибавляют длину отрезка y, равную, например, 87,6 м и получают YA = 66200,0 + 87,6 м = 66287,6.
Рис. 4
6) Расстояние между точками А и В (рис.4) измеряется циркулем, а значение длины линии АВ определяют по поперечному масштабу,
в) с помощью транспортира по плану можно измерить дирекционный угол линии АВ (рис.4)
Дирекционным углом () называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана или линии ему параллельной (на плане это вертикальные линии координатной сетки) по ходу часовой стрелки до направления данной линии. Дирекционный угол может иметь значения от 0° до 360° (рис.5).
Румбом называется острый горизонтальный угол между северным или южным направлением осевого меридиана (либо линии ему параллельной) и направлением данной линии. Румбы могут иметь значение от 0° до 90° и сопровождаются названием четверти, в которой находится линия (рис.5). На рисунке представлены румбы четырех линий А1, А2, A3 и A4:CB:r1,ЮВ;r2, ЮЗ:r3 и СЗ:r4.
Рис.5
Формулы перехода от дирекционных углов к румбам приведены в табл. 1.
Таблица 1
Связь дирекционных углов и румбов
Дирекционные углы |
Название четверти |
Румбы |
0° - 90° 90° - 180° 180° - 270° 270° - 360° |
СВ ЮВ ЮЗ СЗ |
r1 = α1 r2 = 180° - α2 r3 = α3 -180° r4 = 360° - α4 |
г) определение отметок точек, лежащих между горизонталями. На топографических планах рельеф местности изображается горизонталями. Горизонталями называются замкнутые кривые линии, проходящие через точки местности с одинаковыми высотами.
Расстояние по отвесной линии между двумя горизонтальными секущими плоскостями называется высотой сечения рельефа h. На топографическом плане масштаба 1:2000 горизонтали проведены с высотой сечения рельефа равной 1 м.
Расстояние d (рис.6) на плане между двумя соседними горизонталями называется заложением. Чем положе скат, тем больше заложение и наоборот.
Если точка лежит на горизонтали, то её отметка (высота) равна отметке этой горизонтали.
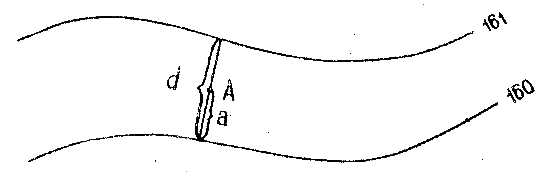
Рис.6
Расстояние d (рис.6) на плане между двумя соседними горизонталями называется заложением. Чем положе скат, тем больше заложение и наоборот.
Если точка лежит на горизонтали, то её отметка (высота) равна отметке этой горизонтали.
Отметку точки А, расположенной на плане между горизонталями, например, с отметками 160 м и 161 м (рис.6), можно определить, измерив в масштабе плана заложение d и расстояние а от первой горизонтали (с отметкой 160 м) до точки.
НА = H1 + h,
где H1- отметка первой горизонтали;
h - превышение точки А над первой горизонталью
h = a/d • h,
где h - высота сечения рельефа, равная в примере 1 м.
При значении d = 50 м и а = 25 м получим
д) определение уклона линии (U) между горизонталями.
Крутизна ската характеризуется уклоном линии местности, т.е. тангенсом угла наклона этой линии к горизонту.
U = tg v =h/d.
Для нашего примера U = 1м/50 м = 0,020.