Граничні умови

Співвідношення, яке показує зв'язок між значеннями векторів електромагнітного поля в різних середовищах на поверхні розділу, називають граничними умовами.

На границях розділу середовищ з різними параметрами поля терплять розрив. Тоді р-ня Максвела використати не можна, оскільки розривні функції не можна диференціювати.

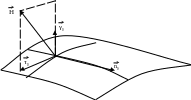
Розглянемо так звані граничні умови. Але спочатку визначимо деякі поняття.

Н ехай , а - співпадає з проекцією вектора на S.

Тоді

(це є відповідно нормальна + тангенціальна складові).

На межі розподілу середовищ можуть розміщуватись мікроскопічні носії заряду, як нерухомі так і утворюючі струм провідності. В мікроскопічній електродинаміці припускається, що заряди не займають об’єму, а є поверхневими. Тоді густиною поверхневого заряду називають величину:

(Кл/м )

А поверхневий струм це є:

j (А/м)

Граничні умови електричного поля:

1. або ,

тобто в граничних точках різниця нормальних компонент вектора в обох середовищах рівна густині поверхневого заряду. Якщо ж =0, то нормальна компонента залишається неперервною.

2. або , ,

тобто, тангенціальна компонента вектора залишається неперервною. Ще записують її так:

Граничні умови магнітного поля:

1. або ,

Тобто, нормальна компонента вектора магнітної індукції завжди неперервна.

2. або j

Тобто, тангенціальна компонента вектора неперервна лише при відсутності на границі поверхневого струму.

Частіше використовується еквівалентна гранична умова:

Повна система граничних умов

На поверхні разділу двох середовищ повинні виконуватися слідуючі граничні умови:

Або у векторній формі:

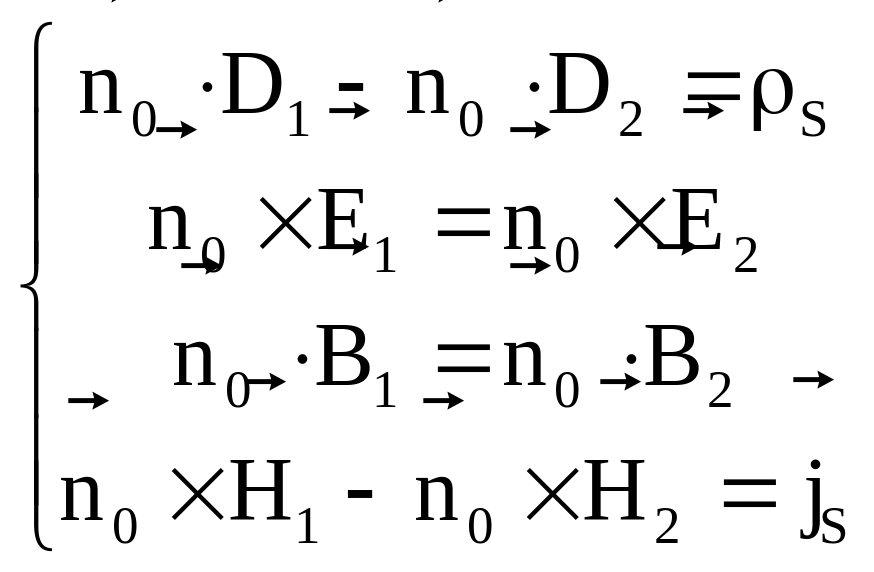
ПРИКЛАД 1. Нехай . Тоді або , звідки .

ПРИКЛАД 2. Якщо поле в іншому середовищі відсутнє, тобто , то з або випливає: , тобто підходить до границі по нормалі.

З або також випливає, що , тому вектор підходить до межі по дотичній. Подальше використання граничних умов або , і дає: тобто, існування поля в середовищі 1 при його відсутності в середовищі 2 зумовлено поверхневими зарядами і струмами.

Лекція 5. Основні рівняння електродинаміки. Рівняння Максвелла

Всі електромагнітні явища описуються системою з|із| чотирьох рівнянь.

До середини XIX століття|віку| вчені відкрили|відчиняли| цілий ряд|лаву| законів, що описують електричні і магнітні явища і зв'язки між ними. Зокрема, були відомі:

• закон Кулона (1785), що описує силу взаємодії між електричними зарядами

• теорема Гаусса (1813), що унеможливлює існування в природі ізольованих магнітних зарядів (магнітних монополів)

• закон Біо-Савара (1820) описує магнітні поля, що породжуються рухомими електричними зарядами.

• закони електромагнітної індукції Фарадея (1831) згідно яким зміна магнітного потоку породжує електричне поле і індукує струм в провідниках.

Ці чотири групи законів і були узагальнені Джеймсом Клерком Максвеллом (1864), якому вдалося об'єднати їх в струнку систему (що отримала його ім'я), що складається з чотирьох рівнянь і вичерпним чином описує всі вимірні характеристики електромагнітних полів і електричних струмів, яка названа його ім'ям. Перш за все, Максвеллу ми зобов'язані строгим математичним описом всіх відомих законів електромагнетизму (Фарадей, наприклад, взагалі формулював всі відкриті ним закони виключно в словесній формі). По-друге, до сформульованої ним системи Максвелл вніс немало принципово нових ідей, відсутніх в початкових законах. По-третє, він додав всім електромагнітним явищам строге теоретичне обгрунтування. І, нарешті, по-четверте, на основі складеної ним системи рівнянь Максвел зробили ряд важливих прогнозів і відкриттів, включаючи прогноз існування спектра электромагнітного випромінювання.