Міністерство транспорту та зв’язку України

Львівський коледж

Державного університету інформаційно-комунікаційних технологій

Конспект лекцій

з навчальної дисципліни: «Технічна електродинаміка»

за напрямком 6.050903 «Телекомунікації»

для спеціальностей освітньо-кваліфікаційного рівня бакалавр

Львів-2010

Лекція 1.Дії над векторами

Вектором називають величину, що характеризується не тільки своїм числовим значенням (довжиною), але й напрямом.

Вектором в тривимірному просторі називають сукупність трьох величин, які змінюються при поворотах системи координат.

Скаляром в тривимірному просторі називають величину, яка не змінює своє значення при поворотах координатної системи.

Якщо фізична величина в кожній точці приймає векторне значення, то поле називають векторним.

= (М), М € D

Якщо фізична величина в кожній точці області приймає певне числове значення, то поле називають скалярним.

u = u (М), М € D

u = u (x,y,z)

Елементи векторного аналізу. Вектори

Модуль вектора : = . Розрізняють: вільні, ковзні і зв’язані вектори. Вільний вектор можна переносити паралельно самому собі у будь-яке місце простору, не змінюючи цим його значення. Ковзний вектор може бути вибраний де завгодно вздовж однієї прямої лінії. У зв’язаному векторі його початок (точка прикладання) завжди зафіксована. Вектори, що лежать на одній або паралельних прямих, називають колінеарними.

Вектори, паралельні одній площині, називають компланарними. Вектори називають рівними, якщо вони колінеарні, мають однакові модулі та однакові напрямки.

В ектори і можна представити як і , де , - одиничні вектори, орти, а числа і - абсолютні значення векторів або модулі векторів і . Орти, що відповідають напрямкам осей X, Y, Z декартової системи координат, позначають через , , , або , , . Вектор можна представити у вигляді розкладу:

де A_x, A_y, A_z - проекції на осі декартової системи координат.

Д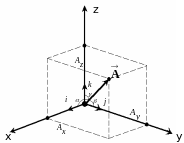 еколи будуть використовуватися векторні складові:

Тоді модуль вектора :

А направляючі косинуси: ;

; та

Додавання векторів

Додавання векторів зводиться до сумування їх компонентів:

;

Скалярний добуток векторів

Скалярний добуток векторів і визначається таким чином:

Властивості:

1 . Якщо вектори , то ;

2. ;

3. ;

4. ;

5. .

6. Якщо , тобто , то вектори і називаються ортогональними

Векторний добуток двох векторів

Векторний добуток векторів і це є:

д е - орт, направлений по нормалі до площини векторів і , причому так, що найменша кутова відстань між їхніми напрямками, позначена , відповідає переміщенню від до за годинниковою стрілкою, якщо дивитися вздовж .

Властивості:

1. Якщо , тобто  , то ;

2. , де - скаляр;

3.

Від перестановки співмножників векторний добуток змінює знак: ;

Скалярні добутки декартових орт:

- для  орт; - для  орт.

Векторні добутки декартових орт:

	 орти
}	 орти

Змішаний (векторно-скалярний) добуток векторів

Для 3-х векторів визначено добуток:

Геометрично це є об’єм паралелепіпеда.

Властивості:

1. При циклічній перестановці векторів множників, змішаний добуток не змінюється: ;

2. При перестановці 2-х співмножників змішаний добуток змінює знак: ;

3. Змішаний добуток дорівнює нулю, якщо - компланарні.

Подвійний векторний добуток

Він розкривається за формулою:

Тут скалярні добутки, що позначені за допомогою круглих дужок, входять як числа.

Лекція 2. Градієнт, дивергенція, ротор.

Градієнт

Н ехай задано скалярне поле . Введемо вектор , що називається градієнтом U, який направлений у сторону максимального збільшення U і рівний швидкості зміни U у цьому напрямку.

Очевидно, що: ,

де - лінія, ортогональна до поверхні рівня.

Маємо також: .

Визначаючи за цією формулою проекції градієнта U в декартовій системі координат :

, , , отримуємо

Скалярне поле U породжує векторне поле . Таке векторне поле називається потенціальним, а скалярна функція – потенціалом. Поверхні рівня, на яких , є еквіпотенціальними поверхнями. Тоді модуль градієнта рівний:

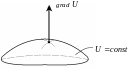
Стрілка градієнта вказує на напрямок найбільшої крутизни.

Тому вода буде стікати протилежно до стрілки – від найбільш крутих місць – вниз. Градієнт ще називають просторовою похідною.