Вопрос 35. Теоретико-автоматная модель и основные понятия шифрованной связи.

Процесс передачи информации в системе шифрованной связи состоит из 3-х последовательных этапов: 1) зашифрование; 2)передача шифрованной информации по КС; 3) расшифрование. Эти процессы могут быть либо разделены во времени, либо происходить одновременно.Условная схема шифрованной связи:

, где X^*. Если нет помех, то такую схему для дискретной информации можно записать как последовательное соединение автоматов: A <-\ A. Тогда ТА-модель выглядит следующим образом:A=(X, KS, Y, h, f), A=(Y, KS, X, h, f) - автоматы, которые удовлетворяют следующим условиям: а) А- инъективен; б) h((k,s),x)=(k,s) k, s, x, т.е. в процессе работы автомата левая координата состояния, не меняется от такта к такту;в) А- стандартный левый обратный к А; г) h((k,s),x)=(k,s) k, s, x, т.е. аналогично б). Из ранее доказанной теоремы (Следующие свойства равносильны: а) А имеет левый обратный; б) А-инъективный; в) sS, f_s: XY- инъективна; если в свойствах а), б), в)- левый заменить на правый, а инъективный на сюръективный, то полученные свойства будут равносильны) =>, что дляА с а) и б) =>  A с в) и г), причем, приX=Y => A- определен однозначно и А=А^-1;

Определение: При условиях а), б), в), г) пара автоматов: (A, A)- автоматная шифр. система (ШС). Опишем ранее известные параметры на языке ШС:X- открытый шифр; Y- шифр. алфавит; (KS)- множ-во ключей; K- множ-во долговременных ключей; S- множ-во разовых ключей; A- шифратор передачи; A- шифратор приема; f_(k,s): XY- частичные функции-суммарный шифрпри ключе (k,s), т.е.f_(k,s)(x_i)=y_i. Процесс шифрования открытого сообщенияX^* происходит следующим образом: для шифраторов А и Ав качестве начальных состояний устанавливается один и то же ключ: (k,s) при этом шифраторы синхронизируются. Далее открытое сообщениеподается на вход шифратора передачи – А и перерабатывается в криптограмму- вых. последовательность А при начальном состоянии (k,s). через КС подается на вход шифратора приема - Аи расшифровывается в открытое сообщение: =A_(k,s)()=A_(k,s)(A_(k,s)()). При этом необходимо сделать некоторые замечания:1) реальная шифроаппаратура может работать в разных режимах: -шифрования (основной режим); - синхронизация; далее будем рассматривать только режим шифрования.2) -открытое сообщение (открытая информация+служебная информация).В реальной ситуации далеко не все последовательности из X^*- могут быть открытыми сообщениями, т.е.0X^*, но это очень усложняет рассуждения => предпологаем, что X^*. 3)Обобщая введенную модель, можно отказаться от условий в) и г) и считать А- произвольным левым обратным к А (не обязательно стандартный), однако, в наиболее интересных случаях: X=Y => левый обратный к А- стандартный обратный к А + ключи на приеме и передаче совпадают => не обобщаем.4)Во введенной модели предполагается, что некоторая часть ключа (k,s)- может быть несекретной, т.е. вообще передаваться в КС. 5) При использовании в шифраторах приема узлов с большой вероятностью самовосстановления (А-самовосстановления) соответствующие этим блокам части разовых ключей на приеме и передаче могут быть различены в какие-то моменты времени, т.к. через небольшое кол-во тактов они станут одинаковы с большой вероятностью. (т.е. эту часть можно не синхронизировать).

Долговременный ключ от текста к тексту не меняется => kK A_k-внутренний подавтомат А с множ-вом состояний: {k}S; A_k- внутренний подавтомат Ас множ-вом состояний: {k}S - это корректно в силу б) и г), тогда А=; А=, причем: A_k- стандартный левый обратный к А_k, тогда A_k- шифратор передачи при долговременном ключе k, A_k- шифратор приема при долговременном ключе k =>, а А_k- стандартный правый обратный к А_k, тогда шифраторы приема/передачи представляются в виде:

(1)(1) – реализуютh_k автомата А_k; (2) и (2)- автоматы БП, реализующиеf_k, f_k. На процесс шифрования можно смотреть как на процесс выработки суммарных шифров: вi-ом такте вырабатываетсяf_(k,s)(x_i)=y_i. В соответствии с теоремой1: все суммарные шифры - инъективные отображения, а приX=Y-биекции иf_(k,s)=f^-1_(k,s). Рассмотрим один из подходов к реализацииf и f: Пусть Г- некоторое множ-во, Г<, и пусть: KSГ- отображение из множ-ва ключей в Г, пустьG: ГXY, причемG-инъективная поxфункция. =>  G: ГYX: G(,G(,x))=x, ,x {обратная слева кG по второй переменной} => Блоки (2) и (2) строятся следующим образом:

Блоки GиG'- шифрующие блоки. При X=Y={0,1} => f=f- всегда совпадают иf_k(s,x)=_k(s)x. Пусть X=Y; X>2. Метод построения шифрующих блоков (метод образующих) состоит из следующих этапов:а) выбираем L=(Z, X, g)- автомат без выхода, подстановочный;б)фиксируем: lN- достаточно большое;в)выбираем: _k:KSГ, где Г=Z^l;- эти вектора- управляющие комбинации, аl-длина управляющей комбинации;г)f_k(s,x)=g_(s)(x)=g_z… g_z(x);- финальное состояние автоматаLпри начальном состоянииxи входной последовательности (z₁,…,z_l), тогда_k(x)=(z₁,…,z_l), f_k(s,x)= g_z… g_z(x)- финальное состояние реверса автомата L при начальном состоянииxи подаче на вход управляющей комбинации в обратной последовательности:

Наибольшее распределение получил случай, когда: X=Y={0,1}; Z={0,1}; Z=R().

Определение: Шифросистема (А, А) -называется ШСгаммирования, если ее суммарные шифры обладают следующим свойством: (k,s), (k,s)KS: (f_(k,s) f_(k,s)) => f_(k,s)(x) ₎f_(k,s)(x) xX, => для таких шифросистем, зная один только переход, например,f_(k,s)(x)=y, т.е.xy, тогда f_(k,s)- определяется однозначно и { f_(k,s)(k,s)KS}Y; всегоf_(k,s)- число размещений из YпоX: (Y!) / (Y-X)!.

Определение: шиифросистема инволютивная (обратимая) -если шифраторы приема и передачи совпадают.

Утверждение(критерий инвалютивности ШС):Шифросистема (А, А)- инволютивна X=Y, (k,s)KS, xX: а) f^-1_(k,s)=f_(k,s) (т.е. все суммарные шифры- инволюции, т.е.f²=e, т.е. порядок подстановки2 (т.е. из циклов длины 1 или 2)); б) h((k,s),f((k,s),x))=h((k,s),x). Доказательство:"<=" : Из а), б), и условия => А=А^-1, т.к.X=Y, а из свойств а) и б) – по построению стандартного обратного => A^-1=A;"=>" : Если А=А, тоX=Y => A=A^-1- стандартный обратный к А, а по построению стандартного обратного из свойства инволютивности шифросистемы => а) и б).

Для (k,s), (k,s)KS: рассмотрим следующие утверждения: 1* - (k,s)~ (k,s) в А;2* - (k,s)~ (k,s) в А3* - А_(k,s)A_(k,s)=E_X* (E_X*- тождественное преобразование множ-ваX^*). Очевидны следующие импликации: 1* => 3* (из определения левого (правого) обратного),2* => 3*. При X=Y- все 3 свойства равносильны (т.к. А=А^-1).

Определение: Ключи (k,s), (k,s)- эквивалентные на передаче, если выполнено свойство 1*; эквивалентные на приеме, если выполнено 2*;и, если выполнено 3*, то (k,s)- ключ расшифрованиядля (k,s). Число(А)-число неэквивалентных ключей на передаче; Число(А)-число неэквивалентных ключей на приеме, при этом, еслиX=Y, то‘на приеме’ и ’на пердаче’ можно опустить.

Определение:Долговременные ключиk, k шифросистемы (А, А)-эквивалентные на передаче (приеме), еслиA_k~A_k (A_k~A_k). Если в двух предшествующих определниях заменить‘~’ на‘’, то приходим к более общему понятию - эквивалентность ключей с задержкой, которое представляет особый интерес для шифраторов с блоками- автоматами самовосстановления.

Определение: Ключи (k,s), (k,s)- изоэквивалентные (эквивалентные на приеме с точностью до простой замены), если биекции g₁: XX, g₂: YY: g₁^*A_(k,s)g₂^*=A_(k,s), гдеg^*(y₁,…,y_l)=(g(y₁),…,g(y_l)).

Под Близкими ключами понимают ключи, которым при расшифрованиисоответствуют близкие в том или ином понимании открытые сообщения. Ключ(k,s) называется-близкийк(k,s) на длине l,если нормированное расстояние Хеминга: (, A_(k,s)A_(k,s)()), X^l, (т.е. с p=1), и 01. В частности, приX=Y понятие-близости на длинеl совпадает с понятиемl-эквмвалентности. Пусть P_l- некоторое вероятностное распределение на множ-веSX^l. введем следующую величину: d_k,k: SX^l[0,1], гдеd_k,k(s, )=(, A_(k,s)A_(k,s)())- близость между открытым сообщением и расшифрованным с помощьюk₁. Дляk,kK, и ,[0,1] рассмотрим неравенства: 4* P_l(d_k,k)1-; 5* E_l(d_k,k) Определение: Ключk- -близкий на длине lк ключуkс уровнем, если выполнено неравенство 4*; и-близкий на длинеl в среднем, если выполнено неравенство 5*.Заметим, что все рассмотренные бинарные отношения на множ-ве KSилиK-бинарные отношения эквивалентности, кроме отношений-близость.

Рассмотрим следующие неравенства: 6* (А)m(A)l(A) и 7* (А)m(A)l(A). ЕслиX=Y => A=A^-1, (А)= (А), m(A)= m(A), l(A)= l(A).

Определение: длина различимости(A)-этоmin l: 2-х неэквивалентных ключей: (k',s') не ~(k,s) в А существует хотя бы одно открытое сообщение длинныl, X^l, что А_(k,s)()A_(k,s)(). Другими словами, приl<(A)-есть хотя бы пара неэквивалентных ключей в А, которые все открытые сообщения длиныl шифруют одинаково. Приl<(A)- по паре: (открытое сообщение; шифрованное сообщение)- невозможно найти p=1ключей.] A=;A_k- состоянияS => (A)2S-1.

Определение: длина единственностиl(A)- это min l0, такое, что все входные последовательности- диагностические, т.е.(k',s') не~ (k,s) в А и X^l выполняется неравенство A_(k,s)()A_(k,s)(). Другими словами при длинеll(A) по любому X^l и соответствующих =A_(k,s)( ) ключ(k,s) определен однозначно с точностью до эквивалентности. С другой стороны: Приl<l(A) хотя бы одна пара (открытое сообщение;шифрованное сообщение), по которой вы не найдете ключа с точностью до эквивалентности. Для шифросистем: колонной замены или гаммирования – неравенства 6* и 7* обращаются в равенство => l(A)< иl(A)=(A) соответственно.

Пусть m=m(A)< (память), т.е.  : X^mY^m+1X и для (k,s)KxS, и для(y₁,…,y_l)Y^l, lm+1, выполняется неравенство x_m+1,…,x_l= M()_{(x,…,x,y,…,y)} (y_m+1,…,y_l), гдеx₁,…,x_l=А_(k,s)(y₁,…,y_l). Начиная сm+1 такта шифратор приема можно заменить на автомат М(П):

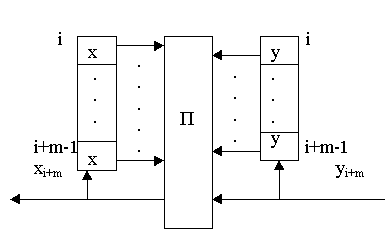
Если мы можем реализовать такую процедуру, то говорят, что мы производим бесключевое чтение вперед. Если A-подстановочный, то памятьm(A') = m(revA'), - функция памяти revA; Имеем кусок открытого сообщения (x_i,...,x_i+m-1):

• Безключевое чтение назад. Для невозможности реализации этого метода необходимо, чтобы память была достаточно большой:mlog_|x|(|K|x|S|).