Задание 5. Частные масштабы по меридиану и параллели.

В задании дана равноугольная коническая проекция (проекция Ламберта). Ее идея заключается в том, чтобы аналогично проекции Меркатора растянуть меридианы в такой же степени, в какой растянуты параллели для обеспечения условий равноугольности (m=n).

Для определения частного масштаба в любой точке карты необходимо:

- определить постоянные проекци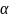и и

- определить масштаб в точке с широтой

Расчеты.

B₁ = 37˚ ₁ = 36, 861757˚

В₂ = 65˚ ₂ = 64, 889832˚

r₁ = Rcos 1 r₁ = 0, 800085

r₂ = Rcos 2 r₂ = 0, 424360

u₁ = tg 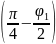u₁ = 1, 999645

u₂ = tg u₂ = 4, 490275

Определим постоянные проекции.

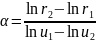
= 0, 783905

= arcsin

= 51, 619558˚

=

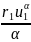
= 1,757078

Определим масштабы на карте на КПМ

= 34,933075˚

r = cos

r = 0,819821

= 1,054438

m = n = = 1,008243

Задание 6. Приближенные значения прямоугольных координат Гауса – Крюгера.

Проекция Гауса – Крюгера – это равноугольная поперечная многолистная цилиндрическая проекция эллипсоида. На эллиптический цилиндр, касающийся глобуса по заданному меридиану, проектируется только узкая полоса шириной 6˚ по долготе. Каждая зона проектируется на свой цилиндр. Всего 60 зон, нумеруемых к востоку от гринвичского меридиана. Средний меридиан каждой зоны с номером N имеет долготу _ср

Расчеты.

B = 44˚05,7' = 43,951258˚

L = 015˚21,9' = 015,365000˚

N 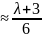= 3

_ср = 6 · 3 - 3˚ = 15˚

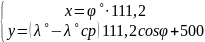
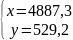
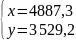
А = 133,604713˚

= А –

= ( – _ср) sin

= 0,253327

= 133,351386˚ = 133˚21'05''

Задание 7. Расчет геодезических координат порога ВПП.

Порог ВПП – начало той части ВПП, которая может использоваться для посадки ВС.

В_ВПП = 51˚ 13' 42,22'' = 51, 228394˚

L_ВПП = -122˚ 37' 16,40'' = -122, 621222˚

= 127˚ 43,2' = 127, 72˚

Длина ВПП = 3250 м

= 2570, 78 м

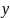= -1988, 36 м

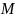= 6374415, 61

W =

W = 0, 997964

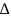В =

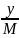
В = -0,000311928 рад =-0, 017872169˚

В₂ = В₁ + ∆В

В₂ = 51, 21052183˚ = 51˚ 12' 37, 88''

r = NcosB

N =

N = 6391260, 01 м

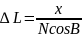
= 0, 000642322 рад = 0, 0366802374˚

₂= L₁ + ∆L

L₂ = -122, 5844196˚ = -122˚35' 03, 91''

Задание 8. Пересчет координат порога впп с ск-95 в пз-90.02.

Для представления аэронавигационных данных и создания карт каждое государство использует геодезическую систему координат, основанную на своем референц-эллипсоиде. (Референц-эллипсоид – эллипсоид, ближе всего подходящий к поверхности геоида на данной территории). Поэтому координаты одной и той же точки в различных системах координат имеют разные значения. И наоборот, одним и тем же значениям широты и долготы соответствуют на картах разных государств различные точки. Расстояния между ними может достигать сотен метров.

В связи с этим в практике авиационного обеспечения полетов возникают задачи, связанные с необходимостью трансформирования координат, т.е. персчета координат точек из одной системы координат в другую.

x = +24,83 м

∆y = -130, 97 м

∆z = -81, 74 м

E_x = E_y = 0

E_z = -0, 6302*10^-6

dm = -0, 22 *10^-6

N = 6391260, 01

B₁ = 51˚ 13' 42,22'' = 51,228394˚

L₁ = -122˚ 37' 16,40'' = -122, 621222˚

Преобразование осуществляется в три этапа:

1. Переход от старых геодезических координат к прямоугольным

x₁ = NcosB1 cosL1 x₁ = -2157581,274

y₁ = NcosB1 sinL1 y₁ = -3370964,3

z₁ = N(1 - ) sinB1 z₁ = 4949582,715

2. Переход от старых прямоугольных координат к новым прямоугольным по формулам Гельмерта.

, где 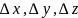– координаты центра старой системы, выраженные в новой

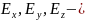углы поворота новой системы вокруг осей x, y, z старой системы, выраженные в радианах

(1+dm) - масштабный множитель

x₂ = (1 + dm) (x ₁ + Ex y 1) + ∆x = -2157553,845

y₂ = (1 + dm) (-E_z x ₁ + y 1) + ∆y = -3371095,888

z₂ = (1 + dm) z₁ + ∆z = 4949499,886

3. Переход от новой прямоугольной к новой геодезической системе координат

D = D = 4002415,031

B₂ = B₂ = 51, 22728156˚ = 51˚13' 38, 21''

L₂ = 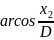L2 = -122, 6198758˚ = -122˚ 37' 11, 55''

Определим радиальную погрешность

r = 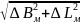r = 156 м

B ∆B'' *31м ∆B = -124, 31м

L ∆L'' * 31м cosB ∆L = -94, 15м

Заключение.

В курсовой работе были рассмотрены вопросы расчета ортодромии и ее элементов, локсодромии, пересчета координат с одного эллипсоида на другой, расчета момента освещения, определения частноортодромических координат S и Z и другие вопросы.

Знания авиационной картографии очень важны: оди дают общее представление о размерах и форме Земли, о небесной сфере и ее элементах.

В этой курсовой работе я получила начальные знания по картографии, ознакомилась с основными определениями, научилась работать по основным формулам.