Задание 2. Расчет частноортодромических координат радиомаяка.

Для автоматизированной коррекции счисленных координат ВС с помощью угломерно-дальномерных радионавигационных систем необходимо заранее определить частноортодромические координаты радиомаяка. Их можно измерить на карте, но точность будет низкой. Более точно их можно рассчитать по формулам сферической тригонометрии.

Расчеты.

Расчет можно выполнить в следующем порядке:

1. Рассчитать путевой угол ортодромии от ИПМ до КПМ.

= 133, 604713˚

2. Рассчитать азимут радиомаяка ( пеленг) от ИПМ по формуле путевого угла ортодромии.

В_р = 40, 475000˚ _р = 40, 332976˚

L_р = 019, 620000˚ λ_р = 019, 620000˚

ctg A_p*=

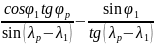
ctgA_p*= -1, 090026

А_р* = -42, 533557˚

Т.к. λ₂> λ₁, А_р* 0, то А_р = 180˚+ А_р*

А_р = 137, 466443˚

3. Рассчитать дальность радиомаяка от ИПМ по формуле длины ортодромии

cosD =

cosD = 0, 996494

D = 4, 799224˚

D = 0, 083762рад

D = 533, 8 км

4. Найти разность = А_р – ₁

∆β = 3, 861730

5. Из прямоугольного сферического треугольника по правилу Непера для рядом лежащих элементов Sр, , D можно записать

Cos = ctg( 90 - Sp) ctgD

ctg(90 - S_p) = tg S_p

tgS_p = cos tgD

S_p = 4, 788378˚

S_p = 0, 083573рад

S_p = 532, 6 км

6. Для не лежащих рядом элементов , D, Z_p можем записать

cos(90 – Zp) = sin sinD

sinZ_p = sin sinD

Z_p = 0, 322846˚

Z_p = 0, 005635 рад

Z_p = 35, 909573 км

Задание3. Расчет элементов локсодромии.

Локсодромия – это кривая на сфере, пересекающая меридианы под постоянным углом, то есть такая линия, в каждой точке которой один и тот же путевой угол.

По форме локсодромия в общем случае представляет собой логарифмическую спираль, асимптотически приближающуюся к полюсам. В частных случаях локсодромия является окружностью ( = 90˚(270˚) ) или меридианом ( = 0˚ (180˚) ).

Путевой угол локсодромии рассчитывается по формуле:

Длину локсодромии можно рассчитать по формуле:

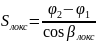
Расчеты.

Путевой угол локсодромии:

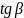*= - 0,924525

* = -0, 746238_рад = -42,756306˚

Т.к. . λ₂> λ₁, β*<0, то β_локс = 180˚ + β*

= 137, 243694˚

Длина локсодромии:

S_локс = 12,282206˚

S_локс = 0,214365 _рад

S_локс = 1366,1 км.

Задание 4. Расчет моментов естественного освещения.

Умение правильно определять наступление моментов естественного освещения имеет в авиации важное значение. В частности, от этого зависит возможность выполнения визуальных полетов, поскольку ночью условия для ведения визуальной ориентировки плохие.

К моментам естественного освещения относятся моменты восхода и захода Солнца, рассвет и наступление темноты.

Местным временем называется время на данном конкретном меридиане.

Гринвичское время – местное время на гринвичском меридиане.

Поясное время – местное время среднего меридиана данного пояса. Земной шар разделен по меридианам на 24 пояса: 0…23.

Расчеты.

, где – склонение солнца в данный день

– широта наблюдателя

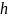= -51' = -0,85˚ ( для восхода/захода)

= -6˚ ( для рассвета/ темноты)

t – часовой угол истинного Солнца в момент восхода и захода на меридиане наблюдателя (истинное местное астрономическое время)

t = t + , – уравнение времени

Т _м = t 12 часов

Т _гр = Т _м – λ

Т _N = Т _гр + N, где N – номер пояса

= 53˚ 15' = 53,25˚

λ = 34˚ 22' = 34, 37˚ = 02.17 ч

= -20,1˚

= +11мин

Моменты восхода/захода :

cos t =0,464

t = 62,37˚ = 4 · ( 62,37) = 250 мин = 04.10 ч

Моменты рассвета/ наступления темноты:

cos t = 0, 304

t = 72,30˚ = 4· ( 72,30) = 289 мин = 04.49 ч

Время	Рассвет	Восход	Заход	Наступление темноты
t	19ч11мин	19ч 50мин	04ч 10мин	04ч49мин
t	19ч 22мин	20ч 01мин	04ч 21мин	05ч 00мин
Tм	07ч 22мин	08ч 01мин	16ч 21 мин	17ч 00мин
Т гр	05ч 05мин	05ч 44мин	14ч 04мин	14ч 43 мин
ТN=4	09ч 05мин	09ч 44мин		18ч 43мин