Практическая часть

Приборы и оборудование

Установка включает в себя следующие блоки: источник питания соленоида, измеритель магнитной индукции Ш1-8 с датчиком Холла на щупе, подставка для щупа, вольтметр, миллиамперметр.

Подготовка к выполнению практической части

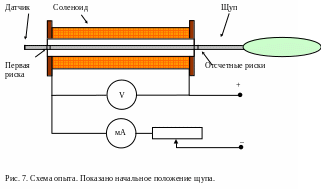
1. Подключить к соленоиду источник питания, реостат, цифровой вольтметр и миллиамперметр (рис. 7).

2. Ознакомиться с порядком работы с измерителем магнитного поля Ш1-8. Включить измеритель поля и проверить начальную калибровку прибора (раздел 5).

3. Подготовить Ш1-8 к работе в составе установки, установив щуп в положение для измерений поля.

Задание 1

Измерение поля в центре соленоида

Цель задания. Ознакомиться с методом измерения магнитных полей в соленоиде. Изучение зависимости поля от тока

1. С помощью линейки определите положение центра соленоида. Поместить щуп так, чтобы датчик оказался в центре соленоида. Координата z указывающая положение датчика Холла устанавливается по шкале на щупе датчика (рис. 7).

2. Включить источник питания.

3. Установить реостат в положение максимального тока. Измерить поле в центре соленоида. Полученный результат записать. Измерить и записать значения тока и напряжения.

4. Уменьшая ток с помощью реостата измерить величину поля при разных значениях I_с. Измерения провести не менее чем для 5 значений тока в диапазоне от максимального тока до минимального значении тока.

5. Используя известную вам программу работы с графиками (Origen, SciDAVis) построить зависимость поля от тока. Аппроксимировать полученный график прямой линией. В пакете Origen уравнение прямой линии записывается в обозначениях: Y = A + B·X. Параметр В или тангенс угла наклона прямой линии даст величину пропорциональную произведению μ₀·n (1.2). В приближении бесконечного соленоида определить n – число витков на единицу длины.

6. Сделать выводы о зависимости поля в соленоиде от тока и о возможных причинах отклонения от уравнения вида Y = B·X.

Задание 2

Исследование распределения поля соленоида

Цель задания. Измерить распределение магнитного поля на оси соленоида.

1. Установить максимальный ток. Поместить щуп в соленоид полностью, так чтобы датчик выдвинулся наружу до первой риски (рис. 7). В этом случае датчик будет измерять поле вне соленоида на расстоянии 7 см от левого на рис. 7 торца соленоида. Измерить величину поля. Значение поля и координаты записать.

2. Перемещая щуп с датчиком вдоль оси соленоида измерить зависимость индукции в соленоиде с интервалом z = 1 см. Отчеты производить по рискам, ориентируясь по правому торцу соленоида (рис. 7) Примечание. Вблизи центра соленоида поле меняется слабо, и перемещать щуп можно сразу на 2 или 3 см. Измерения завершить, когда датчик окажется на расстоянии 7 см перед соленоидом (справа на рис. 7).

3. Результаты всех измерений занести в таблицу. Используя известную вам программу работы с графиками построить зависимость поля вдоль оси соленоида.

4. По данным определите область однородного поля в приближении, когда поле отличается от поля в центре на 1%, 5%, 10%.

Задание 3

Расчет числа витков соленоида

В задании предлагается выполнить расчет соленоида при условии, когда экспериментально измерена величина поля, но число витков неизвестно.

Цель задания. Изучить методы расчета соленоидов. Произвести расчет числа витков соленоида.

1. С помощью линейки с точностью до миллиметра измерить L длину намотки соленоида. Рассчитать число витков в слое: N_слоя = L/d. Диаметр провода обмотки d = 1 мм.

2. Считая что внешний диаметр соленоида D_в = 8 см, а внутренний предварительно считать равным D_вн = 5 см определить число слоев намотки: N_с = ½(D_в - D_вн)/d.

3. Найти предполагаемое число витков соленоида N = N_слоя ·N_с. Зная полное число витков, определить число витков на единицу длины соленоида. Сравнить с полученным значением в задании 1.

4. Пользуясь выражением (1.9) рассчитать величину магнитного поля соленоида для значения тока, которое использовалось в задании 1. Обратите внимание, что в (1.9) входит полудлина соленоида и средний радиус намотки. Определите эти величины.

5. Сравнить с экспериментальным значением поля в центре соленоида. Сделать выводы о возможных причинах расхождения между расчетом и экспериментом.

Задание 4

Измерение сопротивления соленоида и расчет числа витков

1. Используя результат измерения напряжения и тока, полученные в Задании 1, рассчитать по закону Ома сопротивление соленоида.

2. Исходя из величины сопротивления R_ом, вычислить длину провода. Длина провода определяется так: l_r = R_ом·S/ρ, где S = πd²/4 - сечение провода, ρ = 0,017 Ом·мм²/м. Примечание. Исходя из размерности ρ при расчете d берется в мм², при этом l – получится в метрах.

3. Пользуясь методикой приведенной в разделе 2 (1.10) определить длину провода в одном вертикальном слое намотке L_{в c}.

4. Вычислить полную длину провода. l = L_{в c} N_слоя

5. Сравнить расчетную длину l с той, что получилась в результате расчета на основании измерений сопротивления намотки (l_r). Предположив, что расхождение связано с ошибкой определения внутреннего диаметра намотки, варьируя внутренний диаметр намотки, добейтесь совпадения значений длины провода определяемой путем расчета и путем измерения сопротивления. Таким образом, можно определить истинный внутренний диаметр намотки и реальное число слоев намотки.

6. Исходя из полученного значения внутреннего диаметра и методики приведенной в пункте 2 Задание 3, найти число слоев намотки. Окончательно рассчитать полное число витков соленоида.

Задание 5

Расчет распределения поля в соленоиде

Цель задания. Рассчитать теоретическую зависимость поля вдоль оси соленоида и сравнить с результатами эксперимента.

1. По формулам (1.6 – 1.8) рассчитать теоретическую зависимость поля в соленоиде от координаты z. При расчете использовать значение тока такое же, как и в опыте, а также определенные ранее геометрические размеры и число витков.

2. По данным Задания 2 на одном графике постройте экспериментальную и теоретическую зависимости поля от координаты z.

3. Рассчитайте абсолютное и относительное отклонение теоретического значения поля от экспериментального В и В/В в трех точках: в центре, у одного из торцов и в крайней точке вне соленоида.

Примечание: Все расчеты для данной работы удобно проводить в пакете Mathcad.

Литература

1. Физические величины: Справочник/ А.П. Бабичев, и др. Под ред. И.С. Григорьева, Е.З. Михайлова. – М.: Энергоатомиздат. – 1991. – 1232с.

2. Кухлинг Х. Справочник по физике. М.: "МИР". – 1982. – 519с.

1 По закону Стефана – Больцмана мощность Р_{т и} теплового излучения с поверхности составит:

Р_{т и} = ··S(T⁴ – Т⁴_среды),

где  = 5.67·10^-8 Вт/(м²·К) – постоянная,  – излучательная способность, например для черной меди  = 0.78, S – площадь, Т – температура поверхности тела. Р_{т и} = 5.67·10^-8·0.78·1.5·(60-20)⁴ = 0.17 Вт. Например, при T = 150˚С потери за счет излучения составит уже 33 Вт.

2 Э. Холл (амер. физ.) открыл это эффект в 1879 г.

9