3. Порядок расчета соленоида

Предположим, что величина поля в соленоиде задана. Для оценочного расчета можно применить формулу (1.2) для бесконечного соленоида, откуда определяется произведение тока на число витков на единицу длины. Дальнейший расчет сводиться к разделению в этом произведении величины тока и количества витков. А также уточнения всех геометрических величин для реального соленоида. Обычно известен размер объектов, которые будут подвергаться воздействию поля. Геометрический размер объектов определяет минимальный диаметр соленоида и требуемый объем однородного поля. Исходя из протяженности области однородного поля, можно выбрать минимальную длину соленоида, руководствуясь теоретическим выражением распределения поля вдоль оси z (1.6). В первом приближении можно положить, что длина соленоида должна быть втрое больше радиуса. Можно показать, что в этом случае поле в центре реального соленоида будет на 3% меньше поля в бесконечном соленоиде, а протяженность области однородного поля будет порядка диаметра соленоида. Пусть из этих соображений получено, что R₁ – радиус внутреннего отверстия и первого слоя витков соленоида, а L – длина соленоида.

При расчете соленоида, обмотка которого намотана медным проводом, следует учитывать её разогрев при протекании тока. При прохождении тока по проводам, имеющим свободный отвод тепла, например длинные провода в воздухе или в стенах зданий, допустимая плотность тока может достигать 7 - 10 А/мм². Поскольку соседние витки разогревают друг друга, и тепло не успевает рассеяться, то для плотной многослойной намотки допускается меньшая плотность тока. В отсутствии принудительного охлаждения обычно выбирают плотность тока j = 2 – 3 А/мм². При большой плотности тока соленоид просто перегреется и его обмотка сгорит.

При дальнейшем расчете необходимо задаться неким параметром, который выбирают из практических соображений. Часто таковым является диаметр провода. Если выбирают диаметр провода d, то его сечение S = πd²/4. В свою очередь I = j·S. Тогда подставив выражение для тока в (1.2) получим цепочку выражений: B = μ₀j·S·n. В свою очередь число витков на единицу длины n = N/L, где L – длина соленоида, N – общее число витков. Тогда требуемое для получения заданного поля число витков определиться из выражения: N = B·L/μ₀j·S. С другой стороны число витков, которые поместятся на длине соленоида при однослойной намотке N_слоя = L/d. Если окажется, что N > N_слоя, то число слоев определиться N /N_слоя. Теперь можно оценить толщину намотки: h = N·d/N_слоя. Поскольку ранее уже был определен минимальный радиус обмотки, то можно оценить габариты соленоида. Его наибольший радиус будет R₁+h. Если окажется, что средний радиус обмотки R₁+ h/2 таков, что выбранное соотношение длины и радиуса соленоида не удовлетворяет требованию получения нужной однородности поля, то потребуется увеличить длину, с тем чтобы уменьшить число слоев намотки и средний радиус соленоида.

Приведенных расчетов не достаточно, поскольку необходимо увязать их с параметрами источника питания. Из закона Ома I·R_ом = U, где U напряжение источника тока, R_ом – сопротивление соленоида. Если выбрать тонкий провод, то сопротивление обмотки R_ом = ρ·l/S, где l – длина провода в катушке, а ρ – удельное сопротивлении меди (ρ = 0.017 Ом·мм²/м), окажется слишком большим и для питания соленоида потребуется высоковольтный источник. На практике это по многим соображениям неудобно. Поэтому стараются выбрать провод большего сечения, чтобы сделать общее сопротивление обмотки минимальным. С таким расчетом, чтобы уложиться в параметры уже имеющегося промышленного источника питания или не выйти за пределы напряжения нескольких сотен вольт.

Для расчета сопротивления требуется определить реальную длину провода. Наиболее просто длина провода может быть оценена для соленоида, у которого намотано не больше нескольких слоев провода. Тогда можно считать, что в среднем длина провода в одном витке определиться: l_витка = 2π·R_сол, здесь R_сол средний радиус обмотки. В каждом слое поместиться N_слоя = L/d . Тогда полная длина провода определиться l_{провода} = l_витка N_слоя.

Таким образом, зная предполагаемые геометрические размеры соленоида, и задавшись сечением провода можно найти сопротивление обмотки и определить параметры источника питания.

Для многослойной намотки воспользоваться приведенной выше методикой нельзя. Требуется точно рассчитать длину провода в вертикальном слое при спиральной намотке (рис. 2). Длина провода в пределах узкого кольца шириной dr составит dL_{в с} = 2·r·dr/d, где d диаметр провода, а 1/d – число витков на единицу толщины.

L_{в с} = _R1∫^R2 2·r·dr/d = ·(R₂² – R₁²)/d.

Длина спиральной намотки определяется по формуле:

L_{в с} = ·(R₂² – R₁²)/d (1.10)

где R₂ и R₁ соответственно наружный и внутренний радиусы, а d – диаметр провода.

Тогда полная длина провода составит l_{провода} = L_{в с} ·N_слоя.

Сопротивление провода такой длины составит R_ом = ρ ·l_{провода}/S.

Попутно можно определить и массу медного провода m = η_Cu·l_{провода}·S, здесь плотность меди η_Cu = 8960 кг/м³.

Зная ток и напряжение необходимо определить максимальную мощность Р = I·U. Если окажется, что потребляемая соленоидом мощность превышает 1 кВт, то потребуется провести тепловые расчеты, с тем чтобы выяснить потребуется ли принудительное охлаждение магнитной системы.

П отери тепла с поверхности соленоида происходят за счет теплоотдачи и теплового излучения. В условиях теплового равновесия мощность выделяющаяся в обмотке соленоида должна равняться мощности излучаемой с внешней поверхности.

Имеет место уравнение теплового баланса:

Р_э = Р_{т и} + Р_{т о},

где Р_э – электрическая мощность подводимая к соленоиду, Р_{т и} – мощность теплового излучения,

Р_{т о} – мощность теплоотдачи.

Величина отдачи тепла пропорциональна внешней поверхности. Площадь внешней поверхности соленоида S_пов = 2··R₂(l + R₂). Площадь боковой поверхности S_{б пов} = 2··R₂·l.

В электротехнике принято, что температура обмоток на поверхности не должна быть выше 60˚С. Легко показать, что при таких температурах потерями мощности на тепловое излучение можно пренебречь¹.

Отсеется учесть только теплоотдачу в окружающее пространство:

Р₂ = ·S_повT,

где  - коэффициент теплоотдачи. Для воздуха у гладкой стенки коэффициент теплоотдачи

 = 5.6 + 4v Вт/(м²·К),

где v – скорость потока воздуха. Как видно  сильно зависит от скорости воздуха. Именно это обстоятельство используется для охлаждения с помощью вентиляции.

При расчет охлаждения только за счет естественной циркуляции воздуха можно принять, что скорость воздушного потока вокруг соленоида не превысит 1 м/с, что соответствует очень слабому ветру, тогда  = 9.6. В случае принудительного охлаждения с помощью вентилятора можно принять, что скорость воздуха обтекающего соленоид составит 10 м/с (сильный ветер). Тогда α = 45.6 и потери мощности при той же разности температур возрастут в несколько раз.

При необходимости можно оценить температуру внутренних слоев соленоида. Мощность тепла предаваемая через обмотку составит:

P₁ = · S_{б пов} T/h,

где h – толщина намотки,  = 384 Вт/м·К – теплопроводность меди, T – разность температур.

Расчеты обычно показывают, что обычно за счет высокой теплопроводности меди температура внутри и снаружи обмотки различаются незначительно.

При эффективном охлаждении можно увеличивать плотность тока. Но для отвода выделяющегося тепла уже обдува может не хватить и тогда придется прокачивать через обмотку соленоида большое количество воды. При расчетах можно принять, что температура втекающей воды из водопровода будет 15˚С, а вытекающей воды 60˚С. Ежесекундно в объеме должна поглощаться мощность Р_в = Р_э; Р_в = с·m_водΔt, где Δt = 45˚С, с = 4200 Дж/(кг·К) – теплоемкость воды. Отсюда прямо можно определить массу воды, которая должна ежесекундно прокачиваться через соленоид

m_вод = Р_э/с·Δt. m_вод.

Зная секундный расход воды можно рассчитать диаметры трубопроводов и давление в водопроводной сети. Эти расчеты основываются на столь же простых формулах, но поскольку эта тема выходит за пределы работы, то она здесь не рассматривается.

На рис 3. показан примерная конструкция соленоида с водяным охлаждением.

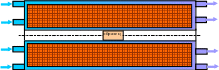
Рис. 3. конструкция соленоида с водяным охлаждением.